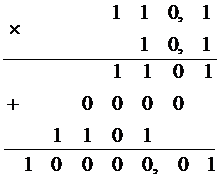I. Действия с двоичными числами.

СИСТЕМЫ СЧИСЛЕНИЯ

Методические указания
для лабораторных работ и контрольных работ
по курсу «Информатика»
для студентов всех специальностей

Электронное издание локального распространения

Регистрационный номер: 060053Э от 20.02.06

Одобрено
редакционно-издательским советом
Саратовского государственного
технического университета

Саратов - 2006

Все права на размножение и распространение в любой форме остаются за разработчиком.

Нелегальное копирование и использование данного продукта запрещено.

Составители: Авдеев Сергей Анатольевич

Под редакцией С.А.Авдеева

Рецензент Ф.С.Селиванов

410054, Саратов, ул. Политехническая, 77

Научно-техническая библиотека СГТУ

тел.: 52-63-81; 52-56-01

http://lib.sstu.ru

Регистрационный номер:

Ó Саратовский государственный

технический университет, 2006

СОДЕРЖАНИЕ:

1. Системы счисления. 4

2. Формы записи числа в позиционной системе счисления. 6

3. Арифметические действия с числами в различных системах счисления. 6

4. Перевод чисел из десятичной системы счисления в другие системы.. 12

5. Перевод чисел из двоичной, восьмеричной и шестнадцатеричной систем счисления в десятичную систему. 20

6. Перевод чисел из восьмеричной системы счисления в двоичную и обратно. 21

7. Перевод чисел из шестнадцатеричной системы счисления в двоичную и обратно 22

8. Нормализованная форма числа. 23

Системы счисления

Система счисления – это способ представления любого числа с помощью алфавита символов, называемых цифрами.

Системы счисления бывают двух видов:

1) непозиционные;

2) позиционные.

В непозиционных системах счисления значимость любого символа (цифры) определяется только его изображением (начертанием) и не зависит от занимаемого им в числе места.

Пример – римская система счисления. Алфавит символов данной системы счисления:

I – единица;

V – пятёрка;

X – десятка;

L – пятьдесят;

C – сотня;

D – пятьсот;

M – тысяча.

Например, год издания одного из учебников по информатике, записанный в римской системе счисления – MCMXCVII – 1997.

В позиционных системах счисления значимость одного и того же символа определяется не только его начертанием (изображением), но и его положением (позицией) в числе.

Пример – арабская или десятичная система счисления. Алфавит данной системы счисления:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

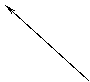1 1 1, 1

разряд десятых (одна десятая)

разряд единиц (единица)

разряд десятков (один десяток)

разряд сотен (одна сотня)

Основанием 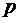позиционной системы счисления называется количество различных символов, используемых для записи чисел данной системы.

Используются четыре различные позиционные системы счисления:

1) Десятичная система счисления. Алфавит представлен выше ( см. стр.10). Он содержит десять символов. Основание 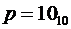. (В правом нижнем углу указывается основание системы счисления, в которой записано данное число. В данном случае читаем: “десять в десятичной системе счисления”.)

2) Двоичная система счисления. Алфавит содержит два символа: 0, 1. Основание 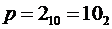(“два в десятичной системе счисления или один ноль – в двоичной”).

3) Восьмеричная система счисления. Алфавит содержит восемь символов: 0, 1, 2, 3, 4, 5, 6, 7. Основание .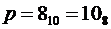

4) Шестнадцатеричная система счисления. Алфавит содержит шестнадцать символов: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, E, F.

Причём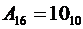

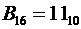
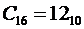
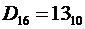
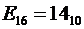
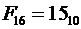
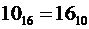
Основание .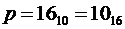

Примеры записи различных чисел:

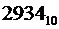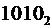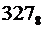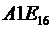Причём, число A1E может существовать только в шестнадцатеричной системе счисления, число 2934 – в десятичной и шестнадцатеричной системах счисления, число 327 – в восьмеричной, десятичной и шестнадцатеричной системах счисления, а число 1010 может существовать в любой из четырёх перечисленных позиционных систем счисления.

Во всех системах счисления кроме десятичной числа принято читать по цифрам (сравните: 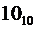– “десять в десятичной системе счисления” и 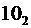– “один ноль в двоичной системе счисления”).

2. Формы записи числа
в позиционной системе счисления

Любое число 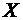в позиционной системе счисления с основанием 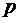может быть записано в двух формах:

1) Свёрнутая форма записи:

,

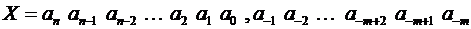целая часть дробная часть

где 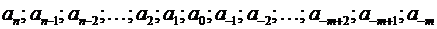– символы алфавита системы счисления;

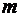– количество разрядов дробной части;

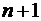– количество разрядов целой части.

2) Развёрнутая форма записи:

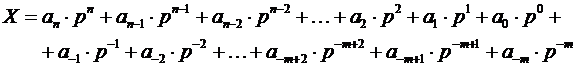
Здесь 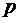– основание системы счисления.

3. Арифметические действия с числами
в различных системах счисления

Сложение двоичных чисел.

Таблица сложения:

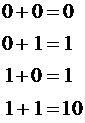
Сложение двоичных чисел удобно проводить столбиком. В случае, когда мы получаем число 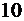, единица переходит в старший разряд.

Пример:

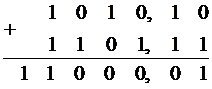
Считаем справа налево:

· ;

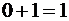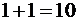· , единица переходит в старший разряд;

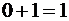· + единица из предыдущего разряда 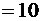, единица переходит в старший разряд;

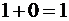· + единица из предыдущего разряда 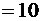, единица переходит в старший разряд;

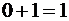· + единица из предыдущего разряда 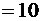, единица переходит в старший разряд;

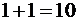· + единица из предыдущего разряда 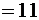, единица переходит в старший разряд.

Вычитание двоичных чисел.

Вычитание двоичных чисел удобно проводить столбиком. Если нужно отнять от нуля, занимаем единицу в старшем разряде. В младший разряд она приходит как двоичное 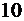. Если имеются промежуточные разряды (содержащие нули), в них остаётся .

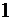Пример:

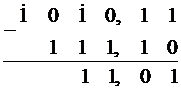
Считаем справа налево:

· ;

· ;

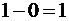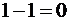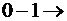· занимаем единицу в старшем разряде ;

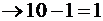· теперь в следующем разряде вместо единицы – ноль 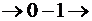в старшем разряде – тоже ноль, занимаем единицу в следующем старшем разряде ;

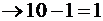· после того, как мы заняли в старшем разряде единицу – в следующем разряде вместо нуля – единица 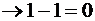(этот ноль уже не записываем).

Для того чтобы сложить два отрицательных числа, нужно сложить их модули, а перед суммой поставить знак “минус”.

Для того чтобы сложить два числа с разными знаками, нужно из большего из двух модулей вычесть меньший, а перед полученной разностью поставить знак числа, модуль которого больше[1].

Пример: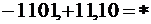

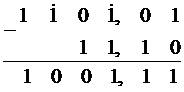
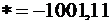
Умножение двоичных чисел.

Таблица умножения:

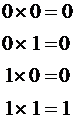
Умножение двоичных чисел также удобно проводить столбиком.

Пример:

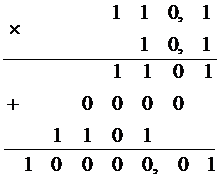
Нормализованная форма числа

В памяти компьютера действительные числа хранятся в нормализованной форме (в нормализованном виде). Для представления десятичного числа в нормализованной форме, его записывают следующим образом:

,

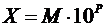где 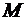– мантисса числа 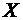, удовлетворяющая условию ;

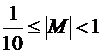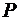– целое число, называемое порядком числа ;

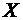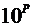– характеристика числа .

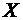Примеры:

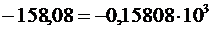
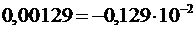
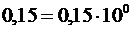
[1] Вернуться обратно, после просмотра на стр. 10;на стр. 11

[2] Вернуться обратно на стр. 20после просмотра

[3] Вернуться обратно на стр. 23 после просмотра

[4] Вернуться обратно на стр. 23 после просмотра

[5] Вернуться обратно на стр. 20 после просмотра

[6] Вернуться обратно на стр. 23 после просмотра

[7] Вернуться обратно на стр. 22 после просмотра

[8] Вернуться обратно на стр. 14 после просмотра

[9] Вернуться обратно на стр. 23 после просмотра

[10] Вернуться обратно на стр. 22после просмотра

[11] Вернуться обратно на стр. 21; стр. 21после просмотра

[12] Вернуться обратно на стр. 23 после просмотра

СИСТЕМЫ СЧИСЛЕНИЯ

Методические указания
для лабораторных работ и контрольных работ
по курсу «Информатика»
для студентов всех специальностей

Электронное издание локального распространения

Регистрационный номер: 060053Э от 20.02.06

Одобрено
редакционно-издательским советом
Саратовского государственного
технического университета

Саратов - 2006

Все права на размножение и распространение в любой форме остаются за разработчиком.

Нелегальное копирование и использование данного продукта запрещено.

Составители: Авдеев Сергей Анатольевич

Под редакцией С.А.Авдеева

Рецензент Ф.С.Селиванов

410054, Саратов, ул. Политехническая, 77

Научно-техническая библиотека СГТУ

тел.: 52-63-81; 52-56-01

http://lib.sstu.ru

Регистрационный номер:

Ó Саратовский государственный

технический университет, 2006

СОДЕРЖАНИЕ:

1. Системы счисления. 4

2. Формы записи числа в позиционной системе счисления. 6

3. Арифметические действия с числами в различных системах счисления. 6

4. Перевод чисел из десятичной системы счисления в другие системы.. 12

5. Перевод чисел из двоичной, восьмеричной и шестнадцатеричной систем счисления в десятичную систему. 20

6. Перевод чисел из восьмеричной системы счисления в двоичную и обратно. 21

7. Перевод чисел из шестнадцатеричной системы счисления в двоичную и обратно 22

8. Нормализованная форма числа. 23

Системы счисления

Система счисления – это способ представления любого числа с помощью алфавита символов, называемых цифрами.

Системы счисления бывают двух видов:

1) непозиционные;

2) позиционные.

В непозиционных системах счисления значимость любого символа (цифры) определяется только его изображением (начертанием) и не зависит от занимаемого им в числе места.

Пример – римская система счисления. Алфавит символов данной системы счисления:

I – единица;

V – пятёрка;

X – десятка;

L – пятьдесят;

C – сотня;

D – пятьсот;

M – тысяча.

Например, год издания одного из учебников по информатике, записанный в римской системе счисления – MCMXCVII – 1997.

В позиционных системах счисления значимость одного и того же символа определяется не только его начертанием (изображением), но и его положением (позицией) в числе.

Пример – арабская или десятичная система счисления. Алфавит данной системы счисления:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

1 1 1, 1

разряд десятых (одна десятая)

разряд единиц (единица)

разряд десятков (один десяток)

разряд сотен (одна сотня)

Основанием 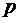позиционной системы счисления называется количество различных символов, используемых для записи чисел данной системы.

Используются четыре различные позиционные системы счисления:

1) Десятичная система счисления. Алфавит представлен выше ( см. стр.10). Он содержит десять символов. Основание 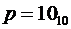. (В правом нижнем углу указывается основание системы счисления, в которой записано данное число. В данном случае читаем: “десять в десятичной системе счисления”.)

2) Двоичная система счисления. Алфавит содержит два символа: 0, 1. Основание 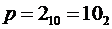(“два в десятичной системе счисления или один ноль – в двоичной”).

3) Восьмеричная система счисления. Алфавит содержит восемь символов: 0, 1, 2, 3, 4, 5, 6, 7. Основание .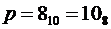

4) Шестнадцатеричная система счисления. Алфавит содержит шестнадцать символов: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, E, F.

Причём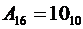

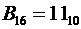
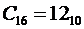
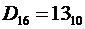
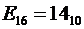
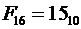
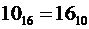
Основание .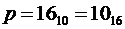

Примеры записи различных чисел:

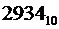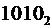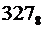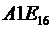Причём, число A1E может существовать только в шестнадцатеричной системе счисления, число 2934 – в десятичной и шестнадцатеричной системах счисления, число 327 – в восьмеричной, десятичной и шестнадцатеричной системах счисления, а число 1010 может существовать в любой из четырёх перечисленных позиционных систем счисления.

Во всех системах счисления кроме десятичной числа принято читать по цифрам (сравните: 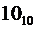– “десять в десятичной системе счисления” и 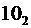– “один ноль в двоичной системе счисления”).

2. Формы записи числа
в позиционной системе счисления

Любое число 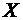в позиционной системе счисления с основанием 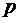может быть записано в двух формах:

1) Свёрнутая форма записи:

,

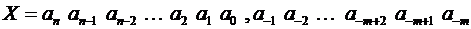целая часть дробная часть

где 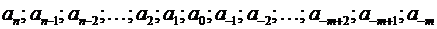– символы алфавита системы счисления;

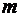– количество разрядов дробной части;

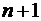– количество разрядов целой части.

2) Развёрнутая форма записи:

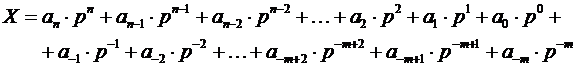
Здесь 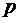– основание системы счисления.

3. Арифметические действия с числами
в различных системах счисления

I. Действия с двоичными числами.

Сложение двоичных чисел.

Таблица сложения:

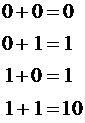
Сложение двоичных чисел удобно проводить столбиком. В случае, когда мы получаем число 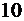, единица переходит в старший разряд.

Пример:

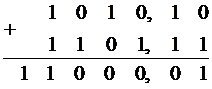
Считаем справа налево:

· ;

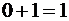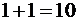· , единица переходит в старший разряд;

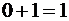· + единица из предыдущего разряда 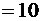, единица переходит в старший разряд;

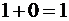· + единица из предыдущего разряда 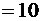, единица переходит в старший разряд;

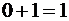· + единица из предыдущего разряда 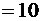, единица переходит в старший разряд;

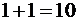· + единица из предыдущего разряда 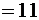, единица переходит в старший разряд.

Вычитание двоичных чисел.

Вычитание двоичных чисел удобно проводить столбиком. Если нужно отнять от нуля, занимаем единицу в старшем разряде. В младший разряд она приходит как двоичное 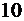. Если имеются промежуточные разряды (содержащие нули), в них остаётся .

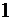Пример:

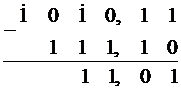
Считаем справа налево:

· ;

· ;

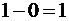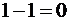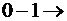· занимаем единицу в старшем разряде ;

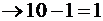· теперь в следующем разряде вместо единицы – ноль 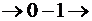в старшем разряде – тоже ноль, занимаем единицу в следующем старшем разряде ;

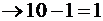· после того, как мы заняли в старшем разряде единицу – в следующем разряде вместо нуля – единица 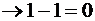(этот ноль уже не записываем).

Для того чтобы сложить два отрицательных числа, нужно сложить их модули, а перед суммой поставить знак “минус”.

Для того чтобы сложить два числа с разными знаками, нужно из большего из двух модулей вычесть меньший, а перед полученной разностью поставить знак числа, модуль которого больше[1].

Пример: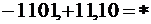

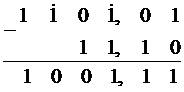
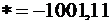
Умножение двоичных чисел.

Таблица умножения:

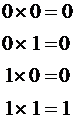
Умножение двоичных чисел также удобно проводить столбиком.

Пример: