Погрешность интерполирования

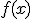Поставим вопрос о том, насколько хорошо интерполяционный полином приближает функцию на отрезке [a,b].
Рассмотри м остаточный член:
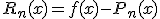, x ∈ [a, b].
По определению интерполяционного полинома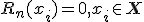
поэтому речь идет об оценке 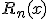при значениях .
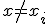Пусть 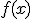имеет непрерывную (n+1) производную на отрезке [a, b].
Тогда погрешность определяется формулой:
,
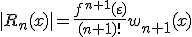где ,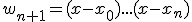
- точка из [a, b].
Так как точка наизвестна, то эта формула позволяет только оценить погрешность:

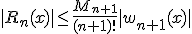
где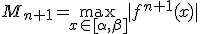
Из вида множетеля следует, что оценка имеет смысл только при 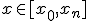. Если это не так, то при интерполяции используются полиномы низких степеней (n = 1,2).

Выбор узлов интерполяции

Так как от выбора узлов завист точность интерполяции, то возникает вопрос о том, как их выбирать. С помощью выбора узлов можно минимизировать значение в оценке погрешности. Эта задача решается с помощью многочлена Чебышева [1]:

В качестве узлов следут взять корни этого многочлена, то есть точки:

Пример

В качастве примера рассмотрим интерполяцию синуса. Возьмем равномерную решетку x = [-3,-1.5,0,1.5,3];
Интерполяция полиномом Лагранжа:

Ошибка(максимальное отклонение от sin(x) на отрезке):0.1423
Интерполяция полиномом Ньютона:
Ошибка:
Возьмем решетку x с узлами в корнях полинома Чебышева= [-2.8531,-1.7632,0,1.7634,2.8532];
Интерполяция полиномом Лагранжа:

Ошибка: 0.0944
Интерполяция полиномом Ньютона:
Ошибка:

Построение кривой по точкам. Интерполяция кубическими сплайнами. Эффективность данного алгоритма. Привести фрагмент программы, поясняющий данный алгоритм.

Интерполяция кубическими сплайнами

Введение

Постановка математической задачи

Одной из основных задач численного анализа является задача об интерполяции функций. Пусть на отрезке 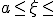задана сетка 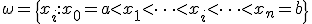и в её узлах заданы значения функции 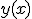, равные 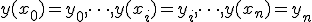. Требуется построить интерполянту — функцию 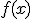, совпадающую с функцией 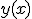в узлах сетки:

( 1 )

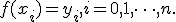
Основная цель интерполяции — получить быстрый (экономичный) алгоритм вычисления значений 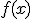для значений , не содержащихся в таблице данных.

Интерполируюшие функции 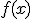, как правило строятся в виде линейных комбинаций некоторых элементарных функций:

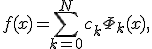
где 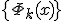— фиксированный линейно независимые функции, 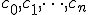— не определенные пока коэффициенты.

Из условия (1) получаем систему из 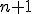уравнений относительно коэффициентов :

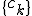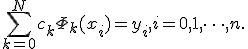
Предположим, что система функций 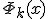такова, что при любом выборе узлов 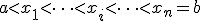отличен от нуля определитель системы:

.

Тогда по заданным 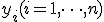однозначно определяются коэффициенты .

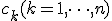Изложение метода

Интерполяция кубическими сплайнами является частным случаем кусочно-полиномиальной интерполцией. В этом специальном случае между любыми двумя соседними узлами функция интерполируется кубическим полиномом.его коэффициенты на каждом интервале определяются из условий сопряжения в узлах:

Кроме того, на границе при и ставятся условия

( 2 )

Будем искать кубический полином в виде

( 3 )

Из условия имеем

( 4 )

Вычислим производные:

и потребуем их непрерывности при :

( 5 )

Общее число неизвестных коэффициентов, очевидно, равно , число уравнений (4) и (5) равно . Недостающие два уравнения получаем из условия (2) при и :

Выражение из (5) , подставляя это выражение в (4) и исключая , получим

Подставив теперь выражения для и в первую формулу (5), после несложных преобразований получаем для определения разностное уравнение второго порядка

( 6 )

С краевыми условиями

( 7 )

Условие эквивалентно условию и уравнению . Разностное уравнение (6) с условиями (7) можно решить методом прогонки, представив в виде системы линейных алгебраических уравнений вида , где вектор соответствует вектору , вектор поэлементно равен правой части уравнения (6), а матрица имеет следующий вид:

где и .

Метод прогонки

Метод прогонки, основан на предположении, что искомые неизвестные связаны рекуррентным соотношением:

( 8 )

Используя это соотношение, выразим и через и подставим в i-e уравнение:

,

где - правая часть i-го уравнения. Это соотношение будет выполняться независимо от решения, если потребовать

Отсюда следует: