Случай равномерного распределения узлов интерполяции

В случае равномерного распределения узлов интерполяции выражаются через расстояние между узлами интерполяции h и начальную точку :

,

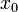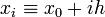и, следовательно,

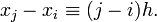
Подставив эти выражения в формулу базисного полинома и вынеся h за знаки перемножения в числителе и знаменателе, получим

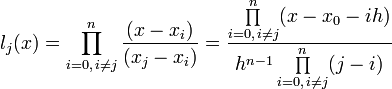
Теперь можно ввести замену переменной

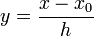
и получить полином от 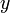, который строится с использованием только целочисленной арифметики. Недостатком данного подхода является факториальная сложность числителя и знаменателя, что требует использования длинной арифметики.

19. Построение кривой по точкам. Интерполяционный полином Ньютона. Эффективность данного алгоритма. Привести фрагмент программы, поясняющий данный алгоритм.

Многочлен Ньютона интерполяционный – как и другие интерполяционные формулы (см. интерполяция), служит для построения многочлена n-й степени, который совпадает в (n+1) точке co значениями неизвестной искомой функции у =f(x).

Пусть в точках х₀, х₁, …, х_n+1 значения функции у = f(x) равны соответственноу₀ = f(x₀), y₁ = f(x₁), …, y_n+1 = f(x_n+1).

Построим интерполяционный многочлен Ньютона с помощью метода неопределенных коэффициентов. Для этого запишем искомый многочлен в виде
P_n(x) = b₀ + b₁(x – x₀) + b₂(x – x₀)(x – x₁) + b₃(x – x₀)(x – x₁)(x – x₂) + … + b_n(x – x₀)…(x – x_n). (1)

Последовательно подставляя в формулу (1) вместо х данные значения х₀, х₁, ...,х_n+1, получим для нахождения неопределенных коэффициентов b₀, b₁, ..., b_n«треугольную» систему уравнений

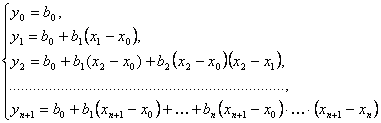
(при подстановке в равенство (1) вместо х числа х₀ в правой части равенства обратились в нуль все слагаемые, кроме первого: там везде был множитель (х – х₀), обратившийся в нуль; при подстановке х = х₁ обратились в нуль все слагаемые, кроме первого и второго – они содержат множитель (х – х₁) и т.д.).

Полученную систему удобно решать: из первого её уравнения находим свободный член искомого многочлена b₀; подставив его во второе уравнение, находим коэффициент b₁ при первой степени х в искомом многочлене:

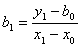
и т.д.

Для интерполяционного многочлена Ньютона можно выписать явные выражения коэффициентов через данные задачи, а также и оценки точности замены неизвестной функции f(x) этим многочленом.

Интерполяция полиномами Лагранжа и Ньютона

Постановка задачи

Пусть задана функция .
Пусть заданы точки из некоторой области .
Пусть значения функции известны только в этих точках.
Точки называют узлами интерполяции.
- шаг интерполяционной сетки.
Задача интерполяции состоит в поиске такой функции из заданного класса функций, что

Метод решения задачи

Полином Лагранжа

Представим интерполяционную функцию в виде полинома

где - полиномы степели n вида:

Очевидно, что принимает значение 1 в точке и 0 в остальных узлах интерполяции. Следовательно в точке исходный полином принимает значение
Таким образом, построенный полином является интерполяционным полиномом для функции на сетке .

Полином Ньютона

Интерполяционный полином в форме Лагранжа не удобен для вычислений тем, что при увеличении числа узлов интерполяции приходится перестраивать весь полином заново.
Перепишем полином Лагранжа в другом виде:

где - полиномы Лагранжа степени i ≤ n.
Пусть
. Этот полином имеет степень i и обращается в нуль при .
Поэтому он представим в виде:
, где - коэффициент при . Так как не входит в , то совпадает с коэффициентом при в полиноме . Таким образом из определения получаем:

где

Препишем формулу в виде

Рекуррентно выражая пролучам окончательную формулу для полинома:

Такое представление полинома удобно для вычисления, потому что увеличение числа узлов на единицу требует добавления только одного слагаемого.