Численное решение уравнения модифицированным методом Ньютона. Эффективность данного алгоритма. Привести фрагмент программы, поясняющий данный алгоритм.

Модифицированный метод Ньютона

Модификация метода Ньютона заключается в замене производной f’(x_n) в точке x_n в формуле

на производную f’(x₀) в точке x₀, т.е. полагаем f’(x_n)≈f’(x₀). В результате получим

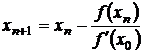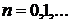( ). (3.23)

Геометрически этот способ означает, что мы заменяем касательные в точках B_n прямыми, параллельными касательной к кривой y=f(x) в точке B₀ (см. рис.3).

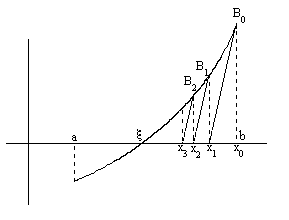
Рис.3. Модифицированный метод Ньютона

Здесь не надо вычислять каждый раз производную f’(x_n). Сходимость процесса (3.23) обеспечивается следующей теоремой.

Теорема 6. Пусть на [a,b] задана дважды дифференцируемая функция f(x), причем выполнены след.условия

а) f(a)f(b)<0

б) f’(x) и f’’(x)≠0 и сохраняют знаки на [a,b].

Тогда исходя из начального приближения 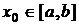удовлетворяющего неравенству

f(x₀)f’’(x₀)>0

можно вычислить модифицированным методом Ньютона единственный корень ξ с любой степенью точности.

Доказательство: Пусть f’(x)>0, f’’(x₀)>0 (см.рис.3) Тогда в качестве x₀ берем точку x₀=b, так как f(b)f’’(b)>0. Из (3.23) следует, что x_n+1<x_n, то есть последовательность {x_n} является убывающей

b=x₀>x₁>…>x_n>a (3.24)

Покажем теперь, что эта последовательность имеет предел ξ. Пусть x_n-1> ξ. Докажем, что x_n> ξ. Для этого запишем n-ое приближение, полученное по формуле Ньютона (см. формулу (3.17)) и по модифицированной формуле Ньютона (3.23)

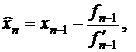
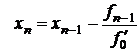
и найдем разность

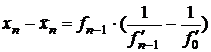. (3.25)

Из теории выпуклых функций известно, что если f’’(x) и сохраняет знак на [a,b], то f(x)является выпуклой. Для выпуклой функции f(x) производная f’(x) является неубывающей, то есть для 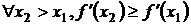. Поэтому

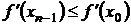. (3.26)

С учетом (3.26) из (11) следует 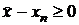. Из теоремы 5 сходимости метода Ньютона мы получали 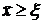, поэтому 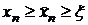. Отсюда

ξ≤x_n. (3.27)

Таким образом, из (3.24) и (3.27) получили убывающую сходящуюся последовательность

x₀>x₁>…>x_n≥ξ.

Следовательно, для любого сколь угодно малого ε>0 можно указать такое n, что

|x_n-ξ|< ε. Теорема доказана.

Сходимость метода. В отличие от метода Ньютона здесь сходимость уже не будет квадратичной. Действительно, из (3.23) имеем

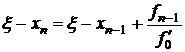. (3.28)

Подставляя (3.21) в (3.28), получим

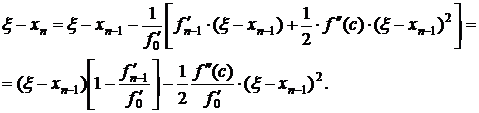(3.29)

Здесь появился линейный член относительно (ξ-x_n-1). При | ξ –x_n-1| << 1 вторым слагаемым в правой части (3.29) можно пренебречь, в результате получим

,

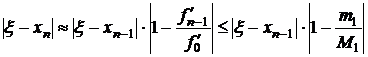где , .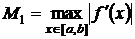

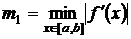Таким образом, сходимость модифицированного метода Ньютона будет линейной с параметром сходимости .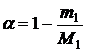

Модифицированный метод Ньютона (метод секущих)

В этом методе для вычисления производных на каждом шаге поиска используется численное дифференцирование по формуле:

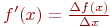
Тогда рекуррентная формула (4.6) будет иметь вид:

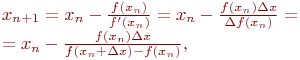(4.10)

где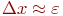

МЕТОД НЬЮТОНА-РАФСОНА

Повышение эффективности метода за счёт использования информации о производной накладывает дополнительные ограничения на функцию. Кроме унимодальности функция должна быть непрерывной и дважды дифференцируемой.

2.5.1. Метод Ньютона-Рафсона.

Пусть - непрерывная и дважды дифференцируемая функция.

Требуется найти корень уравнения .

Зададим – начальную точку поиска. Построим линейную аппроксимацию функции в точке . Для этого разложим в ряд Тейлора в точке и отбросим все члены второго порядка и выше.

Сходимость метода зависит от выбора начальной точки и вида функции.

не сходится

Условие выхода