Основные элементарные функции
1. Степенная функция: 
, где α – действительное число.
2. Показательная функция: 
, где 
.
Показательная функция 
называется экспонентной 
3. Логарифмическая функция: 
, . Функцию 
записывают в виде 
и называют натуральным логарифмом числа х.
4. Тригонометрические функции:
, 
, 
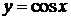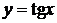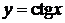
5. Обратные тригонометрические функции:
, 
, 
Графики некоторых функций
Последовательности и их пределы
● Числовой последовательностью 
называется конечное или бесконечное множество чисел 
, расположенных в определенном порядке одно за другим. Числа, входящие в последовательность, называются ее членами. Среди членов последовательности могут быть и одинаковые числа. Последовательность считается заданной, если известен
закон (правило), по которому можно определить любой член последовательности. Этот закон является функцией натурального аргумента и записывается так: 
. Величина 
называется общим (n-ым) членом последовательности.
● Если для данной последовательности 
существует число А, к которому при увеличении n 
числа подходят как угодно близко, то такое число А называется пределом данной последовательности и обозначается 
.
Точная формулировка.
Число А называется пределом числовой последовательности 
, если,
задавая произвольное, как угодно малое положительное число e, можно указать в данной последовательности такое число 
, что все без исключения числа , где 
, будут по абсолютной величине отличаться от А меньше, чем на e: 
для любого .
Случай, когда предел не существует вследствие того, что 
при увеличении n неограниченно возрастает по абсолютной величине, обозначается следующим образом: 
(предел равен бесконечности).
Основные теоремы о пределах последовательностей
1. Последовательность может иметь только один предел.
2. Последовательность, имеющая конечный предел, ограниченная; последовательность, имеющая бесконечный предел, неограниченная.
3. Необходимый и достаточный признак существования предела последовательности. Для того, чтобы последовательность имела предел, необходимо и достаточно, чтобы при задании любого как угодно малого положительного числа 
можно было указать такой ее член , что любые два члена, стоящие после , будут отличаться друг от друга на число, меньшее , т. е.
при 
и 
.
Понятие предела функции
● Функция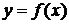 
при 
имеет предел А: 
, если при приближении 
к 
соответствующие значения функции 
подходят как угодно близко к числу А. При значениях 
функция может не принимать значение А и вообще может быть не определена.
Точная формулировка. 
, если задав произвольное как угодно малое 
, можно указать такое число 
, что при любых значени-
ях х в промежутке 
(кроме, может быть, значения )
соответствующие значения будут находиться в промежутке 
, т. е. как только 
, так 
.
Признак Коши. Для того чтобы функция имела предел при , необходимо и достаточно, чтобы для любых двух значений аргумента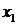 
и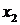 
из области задания функции и достаточно близких к , соответствующие значения функции 
и 
были сколь угодно близки между собой. Из формулировки теоремы следует, что как только 
и 
так выполняется условие 
.
Основные теоремы о пределах
1) Предел постоянной величины С равен этой величине: 
.
2) Если 
и 
– числа, то
3) 
4) 
если 
5) 
6) Монотонная ограниченная функция имеет конечный предел при
любом значении х.
7) Если 
и 
и 
,
то .
Следствие. Чтобы вычислить предел, нужно заменить переменную величину ее предельным значением.
Примеры.
• 
• 