Методы оценки параметра распредеения при статической обработке экспериментального материала.

Для получения оценок используют ряд методов: метод моментов, метод макс.правдоподобия, метод квантилей.

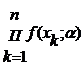1).Метод мах правдоподобия заключается в нахождении оценки наибольшего правдоподобия f (x, α). L( x₁, x₂,…,x_n; α) = ; где x₁; x₂; …x_n; P₁(α);

P₂(α );…;P_n(α); L (x₁, x₂, …, x_n; α ) = 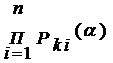Метод макс. правдоподобия заключается в том что за оценку α принимают такое значение при котором функция правдоподобия достигает мах. 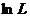: 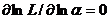Если для параметра α существует эффективная оценка то уравнение правдоподобия имеет единственное решение.

2). Метод моментов состоит в том, что моменты распределения, зависящие от неизвестных вам парам., приравниваются к эмпир. моментам . Взяв число моментов, равное числу неизвестных парам., и составив соответствующие ур-я, получим необход. число ур-й.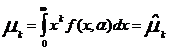

3). Метод квантилей состоит в том, что квантиль теор. распред. приравнивается к эмпир. квантили (если оценке подлежат несколько параметров, то соответствующие уравнения пишутся для нескольких квантилей).

Проверка согласия экспериментального и теоретического распределений при статистической обработке экспериментального материала.

Как бы хорошо ни подобрали теоретическую (вероятностную) кривую распределения, всегда между нею и опытным (статистическим) распределением имеются некоторые расхождения. Желательно установить какой-либо числовой критерий, с помощью которого можно было бы оценить расхождения между теоретическим и экспериментальным распределениями и затем определить, является ли это расхождение случайным или оно – следствие несоответствия теоретического и экспериментального распределений. Меру соответствия теоретического и экспериментального распределений характеризуют какой-либо случайной величиной W, которую называют мерой расхождения. В этом случае критерий согласия представляет собой число, равное вероятности того, что мера расхождения W вследствие случайных причин окажется не меньше ее частного, полученного из опытов значения w, т.е. k = Р (w >> w)На практике за меру расхождения обычно принимают критерии l, c2 , w2. Применение этих критериев основано на использовании так называемой нулевой гипотезы Н0, т.е. гипотезы, утверждающей, что наблюдаемые отклонения объясняются лишь случайными колебаниями в выборках (флуктуациями). Все остальные гипотезы, кроме нулевой, в этом случае называют альтернативными. При этом задаются уровнем значимости α (ошибка первого рода) – ошибкой отклонения верной гипотезы. Ошибка второго рода β – ошибка принятия ложной гипотезы. Величина 1 – β носит название мощности критерия. Выразив эту величину через определенный параметр, можно получить функцию мощности. Выбор значений α и β должен зависеть от последствий совершения ошибок первого и второго рода, причем уменьшить одновременно ошибки первого и второго рода можно только увеличением объема анализируемой выборки.