Спецификация на программу в целом

ТЕХНИЧЕСКОЕ ЗАДАНИЕ

В среде Delphi разработать программу для решения математических задач. Организовать меню программы со следующими обязательными опциями: Задание 1, Задание 2, Выход.

В программе организовать проверку правильности ввода исходных данных.

1. Найти корень уравнения 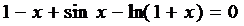, расположенный на найденном отрезке, с абсолютной погрешностью eps. В качестве метода вычисления использовать метод итераций.

2.Составить программу для вычисления суммы ряда с заданной точностью eps и значения функции на заданном диапазоне изменения аргумента (количество расчетных точек – не менее 10)

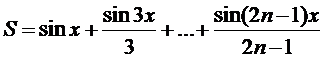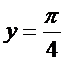, , X [ ; ].

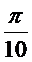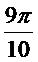ВВЕДЕНИЕ

практической деятельности мы часто сталкиваемся с решением математических задач, которые связаны с большим количеством вычислений, на что уходит много времени и сил. Для ускорения вычисления, создаются программы на различных языках программирования.

Цель моей работы – создание программы для расчета суммы ряда и значения функции при различных значениях аргумента, нахождения корня уравнения на промежутке.

ПОСТАНОВОЧНАЯ ЧАСТЬ

Теоретическое введение

Решение уравнения

В практических вычислениях часто приходится решать уравнения вида: f(x) = 0 ,

где f(x) определена и непрерывна на некотором конечном или бесконечном интервале a < x < b .

Всякое значение х , обращающее функцию f(x) в нуль, называется корнем уравнения. Найти корни уравнения такого вида точно удается лишь в частных случаях. Поэтому разработаны методы приближенного решения уравнений такого вида, такие как: метод итерации, метод Ньютона и метод половинного деления

Метод итерации

Уравнения представляется в виде х=g(x) или в виде х=x+λf(x), где λ-произвольная константа. При этом g(x)= x+λf(x). На отрезке [a,b] выбирается произвольная точка х₀ – нулевое приближение, и принимается в качестве следующего приближения х₁=g(x₀), затем х₂=g(x₁) и так далее х_n=g(x_n-1). Этот процесс последовательного вычисления х_n называется методом итерации.

Если на отрезке [a,b], содержащем корень уравнения, выполнено условие

|g(x) |<q<1, то, увеличивая n можно получить приближение, сколь угодно мало отличающееся от истинного значения корня х. Процесс итерации продолжается до тех пор, пока для двух последовательных приближений x_n-1 и х_n не будет обеспечено выполнение неравенства |х₀ – x_n-1 | < (1-q) ε/q, при этом всегда будет выполнено неравенство |х – x₀ |< ε, где ε – абсолютная погрешность

При нахождении корня нужно при переходе от уравнения f(x)=0 к х=g(x) стремиться представить g(x) так, чтобы производная g(x) по абсолютной величине была возможно меньше 1.

Метод Ньютона

Пусть уравнение f(x)=0 имеет один корень на отрезке [a,b], причем f `(x) и f ``(x) определены, непрерывны и сохраняют постоянные знаки на отрезке [a,b]. В некоторой точке P<sub>0</sub>(x<sub>0</sub>, f(x<sub>0</sub>)), x<sub>0</sub> принадлежит отрезку [a,b], проводят касательную к кривой y= f (x) до пересечения с осью Ох, Абсциссу х<sub>1</sub> точки пересечения можно взять в качестве приближенного значения корня. Проводя касательную через точку P<sub>1</sub>(x<sub>1</sub>, f(x<sub>1</sub>)) и находя новую точку пересечения с осью Ох, получают второе приближение корня х<sub>2</sub>. Аналогично определяют последующие приближения. Уравнение касательной, проходящей через точку P<sub>0</sub> имеет вид Y= f (x<sub>0</sub>)+ f `(x₀)(x – x₀). Полагая y=0, находим абсциссу x₁ точки пересечения касательной с осью Ox: x₁=x₀ – f(x₀)/f `(x<sub>0</sub>). Следующие приближения находят по формуле x<sub>n</sub>=x<sub>n-1</sub> – f(x<sub>n-1</sub>)/f `(x_n-1). Процесс вычислений прекращают при выполнении условия | x_n – x_n-1 | < 2m ε/M , где m – наименьшее значение производной, М – наибольшее значение производной на отрезке [a,b]. При этом условии будет выполнено условие | x – x_n | < ε, для удобства принимают | x_n – x_n-1 | < 10^-4.

Метод половинного деления

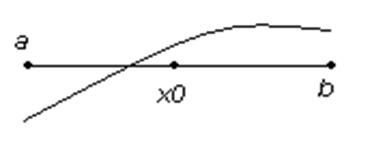
Рисунок 1.1 – Метод половинного деления

Для нахождения корня уравнения, принадлежащего отрезку [a,b], делим отрезок пополам, т.е. выбираем начальное приближение равным х₀ = (a + b) / 2 . Если f(x₀) = 0, то x₀ является корнем уравнения. Если f(x₀) ≠ 0 , то выбираем тот из отрезков [a,х₀] или [х₀,b], на концах которого функция f(x) имеет противоположные знаки. Полученный отрезок снова делим пополам и проводим то же рассмотрение и т.д.

Процесс деления отрезков пополам продолжаем до тех пор, пока

Длина отрезка, на концах которого функция имеет противоположные знаки, не будет меньше наперед заданного числа ε.

Вычисление суммы ряда

Вычисление конечной суммы – нахождение суммы заданного количества слагаемых по формуле.

Также сумму ряда можно найти с помощью рекуррентного соотношения. Если значение слагаемого вычислять по общей формуле, то сложность и время его выполнения оказываются большими, чем при рекуррентном соотношении, где вычисления основаны на полученных ранее промежуточных результатах. Этот способ вычислений более оптимальный.

1. 2. Анализ технического задания

Для нахождения корня уравнения на отрезке я буду использовать метод итераций. Для нахождения суммы ряда каждый член суммы буду вычислять по общей формуле.

Вывод

Ознакомился с методами и приемами решений практических задач. При анализе технического задания выбрали методы и приемы решений. Определили входные данные программы и формы представлений результатов.

РАЗРАБОТОЧНАЯ ЧАСТЬ

Ограничения на программу

Нет

Вывод

Определили структуру программы, входные и выходные данные каждой подпрограммы и их выполняемые функции. Установили ограничения на ввод точности и пунктов меню.

РЕЗУЛЬТАТИВНАЯ ЧАСТЬ

Описание программы

Каждая подпрограмма (отдельная задача) вызывается нажатием кнопки BitBtn1Click (решение уравнения(для Unit1)), BitBtn1Click(нахождение суммы ряда(для Unit2)). В первой задаче находится корень уравнения на промежутке. Для этого в цикле While проверяется на концах промежутка данного отрезка значения функции в соответствующих точках разных знаков. В зависимости от результата сдвигаем ту или иную границу и снова делим взятый нами отрезок пополам. Эту операцию продолжаем до тех пор, пока длина отрезка не станет меньше точности. Затем выводим результат. Во второй задаче с помощью вложенного цикла просчитываем сумму ряда. Во внешнем цикле используется переменная и просчитывается значение функции для соответствующей переменной, во внутреннем – расчетные точки суммы. Результаты выводятся в цикле.

Результаты тестирования

При нормальных условиях программа работает нормально без ошибок.

Программа выводит верные результаты

Вывод

Составили многомодульную программу и дали ее описание. Также дали описание пользовательского интерфейса и инструкцию. Провели тестирование. Программа работает без ошибок и выводит верные результаты.

ЗАКЛЮЧЕНИЕ И ВЫВОДЫ

Программа написана на языке Turbo Pascal 7.0 в соответствии с техническим заданием. Поставив цель, я изучил теоретический материал и ознакомился с приемами и методами решения практических задач. Проанализировав задание, выбрал наиболее удобные методы решений и составил структуру программы. Определил входные и выходные параметры в самой программе и в каждой процедуре. Провел тестирование и получил верные результаты при решении каждой задачи и программа работает без ошибок.

Цель задания достигнута, так как создана программа позволяющая находить корень любого уравнения на любом промежутке (если в программе изменить эти параметры), находить сумму ряда по рекуррентному соотношению и значение любой функции.

ПРИЛОЖЕНИЕ

Текст программы Unit1:

unit Unit1;

interface

uses

Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,

Dialogs, StdCtrls, Buttons, XPMan;

type

TForm1 = class(TForm)

Edit1: TEdit;

Edit2: TEdit;

BitBtn1: TBitBtn;

Label2: TLabel;

ListBox1: TListBox;

Edit3: TEdit;

Label3: TLabel;

Label4: TLabel;

Label1: TLabel;

Label5: TLabel;

Label6: TLabel;

XPManifest1: TXPManifest;

Button1: TButton;

procedure BitBtn1Click(Sender: TObject);

procedure Button1Click(Sender: TObject);

private

{ Private declarations }

public

{ Public declarations }

end;

var

Form1: TForm1;

implementation

uses Unit2;

{$R *.dfm}

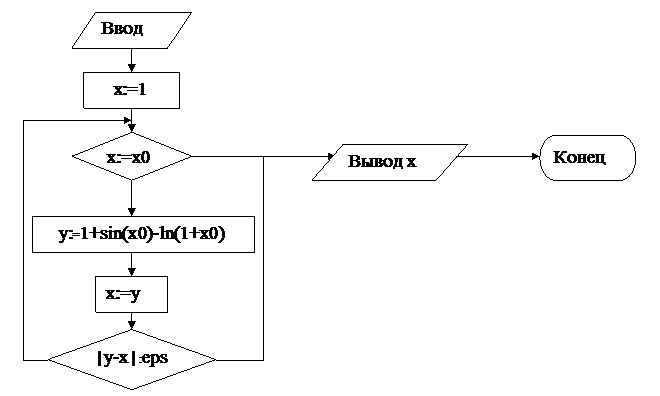
procedure TForm1.BitBtn1Click(Sender: TObject);

var x,x0,d,eps:real;

n:byte;

begin

ListBox1.Clear;

n:=0;

x0:=StrToFloat(Edit1.Text);

eps:=StrToFloat(Edit2.Text);

x:=x0;

repeat

x:=1+sin(x0)-ln(1+x0);

n:=n+1;

d:=abs(x-x0);

x0:=x;

ListBox1.Items.Add(FloatToStr(x));

until d<eps;

Edit3.Text:=FloatToStr(x);

Label2.Caption:=FloatToStr(n);

end;

procedure TForm1.Button1Click(Sender: TObject);

begin

ListBox1.Clear;

Edit3.Clear;

end;

end.

Текст программы Unit2:

unit Unit3;

interface

uses

Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,

Dialogs, StdCtrls, Buttons, Math, XPMan, Grids;

type

TForm3 = class(TForm)

StringGrid1: TStringGrid;

Edit1: TEdit;

Label1: TLabel;

Label2: TLabel;

XPManifest1: TXPManifest;

BitBtn1: TBitBtn;

procedure FormClose(Sender: TObject; var Action: TCloseAction);

procedure BitBtn1Click(Sender: TObject);

procedure FormCreate(Sender: TObject);

private

{ Private declarations }

public

{ Public declarations }

end;

var

Form3: TForm3;

implementation

uses Unit2;

{$R *.dfm}

procedure TForm3.FormClose(Sender: TObject; var Action: TCloseAction);

begin

form2.show;

end;

procedure TForm3.BitBtn1Click(Sender: TObject);

var n,j:integer;

s,eps,x,c:real;

function f(x:integer):integer;

var i,f1:integer;

begin

f1:=1;

for i:=1 to x do f1:=f1*i;

f:=f1;

end;

function y(x:real):real;

begin

y:=pi/4;

end;

begin

eps:=StrToFloat(Edit1.Text);

x:=0.1;

c:=2.4-x

j:=1;

while x<=9*pi/10 do

begin

n:=1;

s:=(sin((2*n-1)*x))/(2*n-1);

while (abs(y(x)-s))>=eps do

begin

n:=n+1;

s:=s+(sin((2*n-1)*x)/(2*n-1));

end;

Stringgrid1.Cells[0,j]:=FloatToStr(x);

StringGrid1.Cells[1,j]:=FloatToStr(pi/4);

StringGrid1.Cells[2,j]:=FloatTostr(s);

j:=j+1;

x:=x+c;

end;

end;

procedure TForm3.FormCreate(Sender: TObject);

begin

StringGrid1.Cells[0,0]:=' x';

StringGrid1.Cells[1,0]:=' y(x)';

StringGrid1.Cells[2,0]:=' Сумма ряда(s)';

end;

end.

БЛОК-СХЕМЫ

Задача 1.

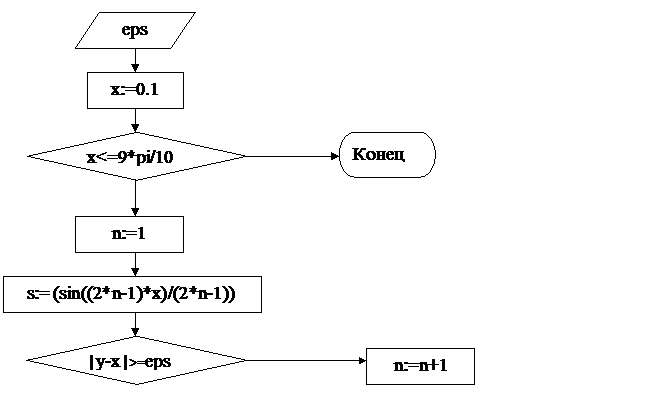
Задача 2.

		n:=1

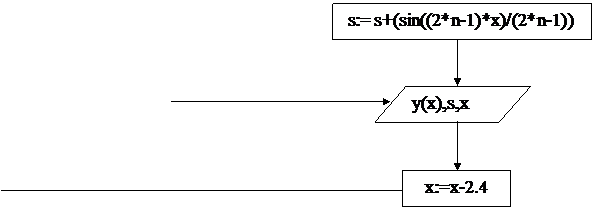ТЕХНИЧЕСКОЕ ЗАДАНИЕ

В среде Delphi разработать программу для решения математических задач. Организовать меню программы со следующими обязательными опциями: Задание 1, Задание 2, Выход.

В программе организовать проверку правильности ввода исходных данных.

1. Найти корень уравнения 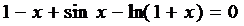, расположенный на найденном отрезке, с абсолютной погрешностью eps. В качестве метода вычисления использовать метод итераций.

2.Составить программу для вычисления суммы ряда с заданной точностью eps и значения функции на заданном диапазоне изменения аргумента (количество расчетных точек – не менее 10)

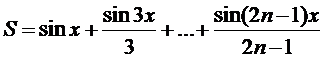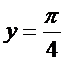, , X [ ; ].

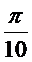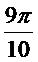ВВЕДЕНИЕ

практической деятельности мы часто сталкиваемся с решением математических задач, которые связаны с большим количеством вычислений, на что уходит много времени и сил. Для ускорения вычисления, создаются программы на различных языках программирования.

Цель моей работы – создание программы для расчета суммы ряда и значения функции при различных значениях аргумента, нахождения корня уравнения на промежутке.

ПОСТАНОВОЧНАЯ ЧАСТЬ

Теоретическое введение

Решение уравнения

В практических вычислениях часто приходится решать уравнения вида: f(x) = 0 ,

где f(x) определена и непрерывна на некотором конечном или бесконечном интервале a < x < b .

Всякое значение х , обращающее функцию f(x) в нуль, называется корнем уравнения. Найти корни уравнения такого вида точно удается лишь в частных случаях. Поэтому разработаны методы приближенного решения уравнений такого вида, такие как: метод итерации, метод Ньютона и метод половинного деления

Метод итерации

Уравнения представляется в виде х=g(x) или в виде х=x+λf(x), где λ-произвольная константа. При этом g(x)= x+λf(x). На отрезке [a,b] выбирается произвольная точка х₀ – нулевое приближение, и принимается в качестве следующего приближения х₁=g(x₀), затем х₂=g(x₁) и так далее х_n=g(x_n-1). Этот процесс последовательного вычисления х_n называется методом итерации.

Если на отрезке [a,b], содержащем корень уравнения, выполнено условие

|g(x) |<q<1, то, увеличивая n можно получить приближение, сколь угодно мало отличающееся от истинного значения корня х. Процесс итерации продолжается до тех пор, пока для двух последовательных приближений x_n-1 и х_n не будет обеспечено выполнение неравенства |х₀ – x_n-1 | < (1-q) ε/q, при этом всегда будет выполнено неравенство |х – x₀ |< ε, где ε – абсолютная погрешность

При нахождении корня нужно при переходе от уравнения f(x)=0 к х=g(x) стремиться представить g(x) так, чтобы производная g(x) по абсолютной величине была возможно меньше 1.

Метод Ньютона

Пусть уравнение f(x)=0 имеет один корень на отрезке [a,b], причем f `(x) и f ``(x) определены, непрерывны и сохраняют постоянные знаки на отрезке [a,b]. В некоторой точке P<sub>0</sub>(x<sub>0</sub>, f(x<sub>0</sub>)), x<sub>0</sub> принадлежит отрезку [a,b], проводят касательную к кривой y= f (x) до пересечения с осью Ох, Абсциссу х<sub>1</sub> точки пересечения можно взять в качестве приближенного значения корня. Проводя касательную через точку P<sub>1</sub>(x<sub>1</sub>, f(x<sub>1</sub>)) и находя новую точку пересечения с осью Ох, получают второе приближение корня х<sub>2</sub>. Аналогично определяют последующие приближения. Уравнение касательной, проходящей через точку P<sub>0</sub> имеет вид Y= f (x<sub>0</sub>)+ f `(x₀)(x – x₀). Полагая y=0, находим абсциссу x₁ точки пересечения касательной с осью Ox: x₁=x₀ – f(x₀)/f `(x<sub>0</sub>). Следующие приближения находят по формуле x<sub>n</sub>=x<sub>n-1</sub> – f(x<sub>n-1</sub>)/f `(x_n-1). Процесс вычислений прекращают при выполнении условия | x_n – x_n-1 | < 2m ε/M , где m – наименьшее значение производной, М – наибольшее значение производной на отрезке [a,b]. При этом условии будет выполнено условие | x – x_n | < ε, для удобства принимают | x_n – x_n-1 | < 10^-4.

Метод половинного деления

Рисунок 1.1 – Метод половинного деления

Для нахождения корня уравнения, принадлежащего отрезку [a,b], делим отрезок пополам, т.е. выбираем начальное приближение равным х₀ = (a + b) / 2 . Если f(x₀) = 0, то x₀ является корнем уравнения. Если f(x₀) ≠ 0 , то выбираем тот из отрезков [a,х₀] или [х₀,b], на концах которого функция f(x) имеет противоположные знаки. Полученный отрезок снова делим пополам и проводим то же рассмотрение и т.д.

Процесс деления отрезков пополам продолжаем до тех пор, пока

Длина отрезка, на концах которого функция имеет противоположные знаки, не будет меньше наперед заданного числа ε.

Вычисление суммы ряда

Вычисление конечной суммы – нахождение суммы заданного количества слагаемых по формуле.

Также сумму ряда можно найти с помощью рекуррентного соотношения. Если значение слагаемого вычислять по общей формуле, то сложность и время его выполнения оказываются большими, чем при рекуррентном соотношении, где вычисления основаны на полученных ранее промежуточных результатах. Этот способ вычислений более оптимальный.

1. 2. Анализ технического задания

Для нахождения корня уравнения на отрезке я буду использовать метод итераций. Для нахождения суммы ряда каждый член суммы буду вычислять по общей формуле.

Спецификация на программу в целом

· Имя модуля: Unit 1

· Имя вызываемого модуля-нет

· Входные параметры: Form: TForm

· Выходные параметры: x, S, Y.

· Выполняемые функции: вывод на экран решений задач

Вывод

Ознакомился с методами и приемами решений практических задач. При анализе технического задания выбрали методы и приемы решений. Определили входные данные программы и формы представлений результатов.

РАЗРАБОТОЧНАЯ ЧАСТЬ