Нормальный алгоритм а.а. маркова

Глава 2

МОДЕЛИ ВЫЧИСЛЕНИЙ

В данной главе рассмотрим различные способы представления вычислений (обработки данных) в виде моделей; эти способы связаны с различной природой вычислений.

Модель – математическая абстракция для класса объектов (процес-сов), в которой выделяются существенные свойства класса и отбрасы-ваются несущественные; чем грубее модель, тем шире класс. Хорошо сформулированная модель обладает ясным физическим смыслом и адек-ватна (соответствует, отвечает требованиям точности) данному классу. Например, в планетарной модели небесные тела представляются в виде материальных точек, не имеющих размеров, но имеющих конкретную массу; эта модель позволяет достаточно точно предсказывать, например, лунные затмения.

Целью построения моделей вычислений является, в первую оче-редь, возможность уточнения понятия ²алгоритм², что необходимо для получения доказательного ответа на главный вопрос теории алгоритмов: существует или нет алгоритм для данного класса задач? С прикладной точки зрения важно также, что подходящая модель вычислений может быть использована и для оценки сложности алгоритма.

Для вычислений в широком смысле построены разнообразные моде-ли, учитывающие характер вычислений (численные, логические, символь-ные), разрядность чисел (битовые либо байтовые), постоянство длины обрабатываемых слов в ЭВМ и т. д.

Ниже рассматриваются 2 модели вычислений в узком смысле:

· ассоциативные исчисления;

· рекурсивные функции,

а также 2 модели дискретной переработки информации – автоматы и машины Тьюринга.

Логические алгоритмы содержат инструкции, относящиеся не к чис-лам, а к объектам любой природы. Примерами логических алгоритмов могут служить алгоритм поиска пути в лабиринте, игровые алгоритмы, алгоритм переключения светофора и т. д. Моделью логических вычис-лений являются ассоциативные исчисления.

Численные алгоритмы сводят решение поставленной задачи к ариф-метическим действиям над числами. Пример — алгоритм Евклида для нахождения наибольшего общего делителя двух заданных положительных чисел. К численным алгоритмам сводится решение многих задач: вычис-ление корней алгебраических уравнений, решение систем уравнений, численное интегрирование и т. п. Моделью таких вычислений являются рекурсивные функции.

Очень широкий класс задач связан с дискретной переработкой информации (символов). Это, например, кодирование и декодирование сообщений. В качестве моделей таких преобразований используются конечные автоматы.

Автоматная модель с расширенными возможностями – машина Тьюринга – позволяет не только реализовать различные вычисления и преобразования информации, но и проверить существование алгоритма для данного класса задач.

Ассоциативные исчисления

Определения, операции, свойства

Исчисление — определённый набор операций над совокупностью математически однородных объектов и правила преобразования этих объектов с использованием данных операций. Примером исчисления, кото-рое широко используется в процессе синтеза логических схем, являются преобразования алгебры логики. Набор правил (аксиом, законов, тождеств) говорит лишь о том, как можно преобразовать исходное булево выражение, но ничего не говорит о том, как надо его преобразовывать (в какой последо-вательности и что делать на каждом шаге), чтобы, например, на заданном логическом базисе получить минимальную задержку схемы. Таким образом, исчисление, в отличие от алгоритма, не содержит указаний, куда нужно идти, чтобы получить результат, а содержит только список допустимых преобразований.

Расширение понятия алгоритма за счёт введения в рассмотрение объектов нечисловой природы связано с ассоциативным исчислением. Ассоциативное исчисление строится на множестве всех слов в данном алфавите с помощью определённой совокупности операций.

Алфавит — любая конечная совокупность различных символов, называемых буквами. Любая конечная совокупность n букв некоторого алфавита является словом длины n в этом алфавите.

Если слово L является частью слова M, то говорят, что слово L входит в слово M.Например, в слове abcbcbad имеются два варианта вхождения слова bcb и одно вхождение слова ba.

В качестве операций ассоциативного исчисления определяется система допустимых подстановок, с помощью которых одни слова преобразуются в другие. Подстановка вида L — M, где L и M — слова в том же алфавите, означает: слово L заменяется на M и наоборот.

Например, пусть имеется алфавит А = {a, b, c}. Рассмотрим слово abcbcbab; к этому слову можно применить подстановку ab - bcb четырьмя способами. Заменяя вхождение ab дважды, получим: bcbcbcbbcb. В то же время к слову bacb эта подстановка не применима.

Рассмотрим особую подстановку P-#. Она означает, что из преоб-разуемого слова удаляется вхождение слова P (оно заменяется пустым символом), а также, что между двумя какими-либо буквами преобра-зуемого слова, впереди него либо за ним, вставляется слово Р. Например, заданы слово dbcd и подстановка abc - #. В результате подстановки получаем: dabcbcd.

Итак, ассоциативное исчисление (АИ) — это множество всех слов в некотором алфавите вместе с конечной системой допустимых подстановок.

Эквивалентность слов.Два слова называют эквивалентными, если одно из них можно получить из другого последовательным приме-нением допустимых подстановок.

Последовательность слов R1, R2, R3, …, Rn, когда каждое слово является результатом однократного применения допустимой подстановки к предыдущему слову, образует дедуктивную цепочку, причём соседние слова в этой цепочке называются смежными. Очевидно, что любые два слова в дедуктивной цепочке являются эквивалентными.

Эквивалентность слов (обозначается L ~ M) обладает всеми свой-ствами отношения эквивалентности — рефлексивностью, симметрич-ностью и транзитивностью.

Если L ~M, то при наличии в каком-либо слове R вхождения L в результате подстановки L - M получается слово R', эквивалентное R. Например, используя эквивалентность acd ~ cad, из слова R = bacdc получаем эквивалентное ему слово R' = bcadc.

В каждом АИ возникает своя специфическая проблема слов, которая заключается в следующем: для любых двух слов в данном исчислении требуется узнать, эквивалентны они или нет. Решение этой проблемы аналогично поиску пути в лабиринте, площадки которого соответствуют смежным словам.

Очевидно, эквивалентность двух слов означает, что соответствующие им площадки связаны некоторым путём, который представляет собой дедук-тивную цепочку от одного слова к другому. Проблема слов является далеко идущим обобщением задачи поиска пути в конечном лабиринте. Так как в любом АИ содержится бесконечное множество различных слов, то соответ-ствующий лабиринт имеет бесконечное число площадок, и, следовательно, решение вопроса об эквивалентности слов сводится к поиску пути в бесконечном лабиринте.

С помощью алгоритма перебора решается ограниченная проблема слов: требуется установить, можно ли одно из заданных слов преобра-зовать в другое применением допустимых подстановок не более чем К раз, где К — произвольное, но фиксированное целое число. Такое ограни-чение в случае лабиринта означает, что расстояние между рассматри-ваемыми площадками не превышает К коридоров.

Однако перебор не подходит для неограниченной проблемы слов. Поэтому для получения желаемых результатов необходимо применять другие идеи, основанные на анализе самого механизма преобразования посредством допустимых подстановок.

В некоторых случаях могут быть обнаружены и использованы свой-ства, остающиеся неизменными для всех слов дедуктивной цепочки (дедуктивные инварианты). На основе дедуктивного инварианта можно установить, какие слова не могут быть эквивалентными.

Проблема слов в АИ имеет большое значение в связи с тем, что к ней сводятся многие геометрические, алгебраические и логические зада-чи. Так, любую формулу логики высказываний и предикатов можно трак-товать как слово в некотором алфавите, содержащем логические сим-волы, высказывания, предикаты и некоторые переменные.

Примеры ассоциативных исчислений

Приведём два примера АИ, точнее, опишем их основные положения.

Исчисление высказываний. Формула называется выводимой в исчислении высказываний, если она может быть получена из конечной совокупности исходных формул путём конечного числа шагов применения правил вывода. Строго доказано, что можно выбрать такую конечную совокупность аксиом исчисления высказываний, из которой выводимы все тождественно истинные формулы. Это важное положение решает проб-лему полноты исчисления высказываний. Процесс эквивалентных преоб-разований или вывода логических следствий может быть представлен как преобразование слов, причём роль допустимых подстановок играют логи-ческие законы и аксиомы.

Таким образом, вопрос выводимости какой-либо формулы становит-ся вопросом существования дедуктивных цепочек, ведущих от слов, пред-ставляющих посылки, к словам, представляющим следствия.

В ряде интерпретаций ассоциативного исчисления, в частности в теории вывода, используются подстановки вида L® M, которые допускают лишь подстановку слева направо (слово L в слово M). Это соответствует лабиринту, по каждому коридору которого можно двигаться только в одном направлении.

В качестве другого примера АИ рассмотрим порождение классов формальных языков(в том числе языков программирования и соответ-ствующих им трансляторов). В теории алгоритмов рассматриваются раз-личные абстрактные системы, предназначенные для моделирования функционирования дискретных систем. Их способность адекватно описы-вать сложное поведение моделируемых систем можно охарактеризовать классами порождаемых ими языков, которые определённым образом кодируют разные возможные способы функционирования систем.

Приведём неформальное описание языка.

В основе каждого языка лежит словарь. Его элементы обычно назы-вают словами, но в теории формальных языков их называют символами. Совокупности слов характеризуются тем, что некоторые из них считаются правильными предложениями языка, а другие — неправильными, или не принадлежащими данному языку. Правильность предложения определяется грамматикой, синтаксисом языка. Синтаксис определяется как множество правил или формул, которые задают множество (формально правильных) предложений.

Любое предложение можно получить из начального символа после-довательным применением правил подстановки.

Синтаксические единицы (грамматические категории) называются нетерминальными символами, а слова в данном алфавите — терми-нальными символами.

Классы языков порождаются конечными множествами правил, назы-ваемых порождающими грамматиками. Каждая грамматика представляет собой набор (A, V, P, S₀),

где А — алфавит терминальных символов;

V — алфавит нетерминальных символов;

P — конечное множество продукций (правил подстановки);

S₀ — начальный символ.

Обозначим А^* (V^*) множество всех слов в алфавите А (V).

Продукция имеет вид a®b, где aÎV*, bÎ(AUV)*. Продукция a®b может быть применена к некоторому слову вида d₁ad₂ и преобразует его к виду d₁ b d₂. Последовательность слов g₀, g₁,…, g_n такая, что слово g_i, 1 £ i £ n, полученное из слова g_i-1 с помощью некоторой продукции из P, называется выводом из данной грамматики, а слово g_n выводимо в ней из слова g₀. Язык, порождаемый грамматикой, — это множество всех терминальных слов (слов из А*), выводимых из слова S₀ с помощью продукций из P.

Конечные автоматы

Автомат - это математическая абстракция, которая предназначена для описания и анализа поведения разнообразных устройств дискретного действия или протекания процессов дискретной обработки информации, для моделирования и построения устройств и процессов. Такая модель успешно используется как в технике (проектирование вычислительных машин, систем управления и связи), так и в других областях деятельности человека - теории и практике административного управления, лингвистике (анализ синтаксиса формального языка, расшифровка древних рукописей) и т. д. Универсальность теории автоматов позволяет рассматривать с единой точки зрения различные объекты, учитывать связи и аналогии между ними, переносить результаты из одной области в другую.

Автомат описывается шестёркой элементов А=(Q, X, Y, d, l,q₁),

где Q = {q₁, q₂,..., q_r} - множество состояний (алфавит состояний);

X = {x₁, x₂,..., x_n} - множество входных символов (входной алфавит);

Y = {y₁, y₂,..., y_m} - множество выходных символов (выходной алфавит);

d - функция переходов, реализующая отображение множества D_d,

D_dÍQ´X, на множество Q (q_p = d(q_j, x_j), q_pÎQ);

l - функция выходов, реализующая отображение множества D_l, D_lÍQ´X, на множество Y (y_d = l(q_j, x_i), y_d Î Y);

q₁ - начальное состояние автомата.

В общем случае автомат может иметь некоторое количество входов и выходов, и тогда каждому входу и каждому выходу может соответствовать свой алфавит. Рассмотрим более простой случай автомата с одним входом и одним выходом.

Автомат называется конечным, если конечны множества Q, X и Y. Автомат называется полностью определённым, если D_d=D_l=Q´X; у частичного автомата функции d и l определены не для всех пар (q_j, x_i)ÎQ´Y.

Символами x_i и y_k обозначают события в процессе или сигналы в устройствах. Иногда используют вместо понятия “символ” понятие “буква”; а последовательность букв называют словом.

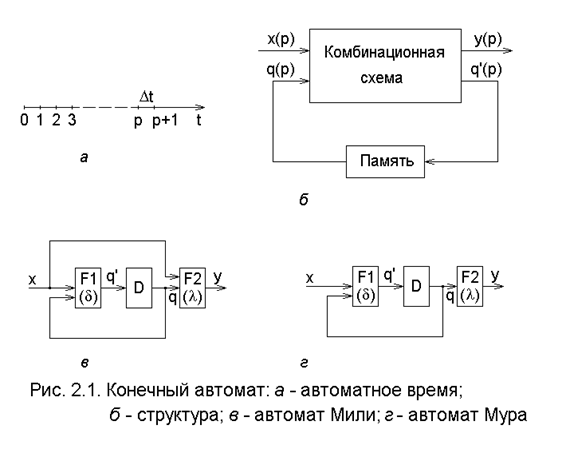
В отличие от привычного рассмотрения времени (время непрерывно и задается на континууме), при изучении и проектировании автоматов удобно рассматривать воображаемое дискретное время (автоматное время, заданное на счётном множестве). Разобьём непрерывную числовую полуось на бесконечное число конечных интервалов, не обязательно равных между собой, и обозначим точки, разделяющие интервалы, неотрицательными целыми числами, начиная с 0 (рис. 2.1,а).

Будем называть дискретным временем t время, которое принимает лишь эти целочисленные значения. Моменты времени, обозначенные числами 0,1,2,..., будем называть тактами.

Отметим, что в реальных условиях сигналы представляются непрерывными функциями времени, поэтому для надежного различения сигналов требуется, чтобы новые значения на входах появлялись после окончания переходных процессов, связанных с предыдущими значениями. При рассмотрении логической структуры автоматов обычно отвлекаются от существа этих процессов и считают, что переменные изменяются мгновенно в тактовые моменты.

Кроме входных и выходных переменных, можно выделить некоторую совокупность промежуточных переменных, которые связаны с внутренней структурой автомата; именно они характеризуют состояние конечного автомата (КА).

При рассмотрении КА значения символов состояний и входов существенны лишь в моменты тактов и несущественны - в промежутках между ними. Поэтому эту модель можно использовать и для описания непрерывных устройств (процессов), если фиксировать значения символов состояний и входов в моменты тактов; при этом важно, чтобы в рассматриваемые дискретные моменты множество возможных состояний было конечным и чтобы удовлетворялось требование однозначной связи между состояниями в соседних тактах.

Понятие “состояние автомата” определяет некоторую предысторию его поведения как реакции на символы, которые поступали ранее на его входы, т. е. состояние соответствует некоторой памяти о прошлом.

Строгое определение понятия состояния связывается с той ролью, которую оно играет при определении конечных автоматов. Во-первых, значение выходной переменной на p-м такте (p-present-настоящее) y(p) однозначно определяется состоянием q(p) и значением входной переменной x(p) на том же такте, т. е. y(p)=l(q(p), x(p)). Во-вторых, состояние q(p+1) в следующем, (p+1)-м такте, однозначно определяется состоянием q(p) и входной переменной x(p) в рассматриваемом такте - q(p+1)=d(q(p), x(p)).

Таким образом, состояние КА в любой тактовый момент характеризуется значением такой переменной, которая вместе с заданным значением входной переменной позволяет определить выходную переменную в данный тактовый момент и состояние в следующий тактовый момент.

Ясно, что автоматы должны обладать способностью сохранять предыдущее состояние до следующего такта, в связи с чем их называют автоматами с памятью (последовательностными машинами). В качестве памяти могут использоваться элементы задержки, на выходах которых повторяются входные воздействия со сдвигом во времени на интервал между тактами Dt.

Термин “состояние” позволяет устранить время как явную переменную и выразить выходные символы как функцию состояний автомата и входов в данный момент (такт). В каждый момент t=0,1,2,... дискретного времени КА находится в определённом состоянии q(t) из множества Q состояний автомата, причём в начальный момент t=0 он всегда находится в начальном состоянии q(0)=q₁. В момент p (рис. 2.1,б), находясь в состоянии q(p), КА способен воспринять на входе символ x(p)ÎX и выдать на выходе сигнал y(p)=l(q(p), x(p)), переходя в состояние q(p+1)=d(q(p), x(p),); q(p)ÎQ, y(p)ÎY.

Таким образом, КА реализует некоторое отображение j множества слов входного алфавита X во множество слов выходного алфавита Y: если на вход автомата, установленного в начальное состояние q₁, подавать некоторую последовательность букв входного алфавита x(0), x(1), x(2),..., т. е. входное слово, то на выходе КА будут последовательно появляться буквы выходного алфавита y(0), y(1), y(2),..., т. е. выходное слово. Относя к каждому входному слову соответствующее ему выходное слово, получим отображение j, индуцированное конечным автоматом.

Автомат без памяти называется тривиальным автоматом, или комбинационной схемой. В таких автоматах значения выходных переменных определяются только комбинацией входных переменных в данный момент; для комбинационных схем функция переходов не имеет смысла, а функция выходов вырождается к виду y(p)=l(x(p)).

На практике наибольшее распространение получили автоматы Мили и Мура, приведенные на рис. 2.1,в и г; здесь: F1 и F2 - комбинационные схемы; D - задержка на один такт (память), q’ - новое (следующее) состояние в момент t = p.

Закон функционирования автомата Мили задается уравнениями:

q(t+1) = d(q(t), x(t)); y(t) = l(q(t), x(t)), t = 0, 1, 2, ..., (2.11)

а автомата Мура -

q(t+1) = d(q(t), x(t)); y(t) = l(q(t)), t = 0, 1, 2, ..., (2.12)

Отметим особенности функционирования автоматов Мили и Мура:

· оба автомата одинаково формируют новое состояние (q, x)®q’, которое затем задерживается на один такт, q(p+1) = q’(p);

· выходной символ в автомате Мили определяется непосредственно входным символом и состоянием в текущий момент t=p ((q, x)®y), а в автомате Мура - только состоянием в текущий момент (q®y) и опосредованно - состоянием и входным символом в предыдущий момент t=p-1 (y(p)=l(q(p)), где q(p)=d(q(p-1), x(p-1)));

· поскольку в автомате Мура выходной символ однозначно определяется его состоянием, то это позволяет идентифицировать состояние автомата по символам на его выходе, т. е. проверять правильность функцио-нирования синтезированного автомата;

· автомат Мили обычно проще (в смысле меньшего числа состояний) эквивалентного ему автомата Мура.

При анализе и синтезе КА используются в основном две стандартные формы представления автомата: табличная и графическая. Рассмотрим эти формы.

Автомат может быть представлен двумя таблицами для каждой из функций d и l либо совмещённой таблицей, несколько отличающейся для автоматов Мили и Мура.

При табличном представлении строки именуются символами состояний, а столбцы - символами входа; в клетках таблиц проставляются символы состояний, причём состояния записываются рядом через разделитель “/” с соответствующими выходными символами: для автомата Мили - в клетках, а для автомата Мура - в именующем столбце.

Для примера табл. 2.1 описывает поведение автомата Мили, а табл. 2.2 - автомата Мура.

Таблица 2.1 Таблица 2.2

A1	x1	x2		A2	x1	x2
q1	q2/y1	q3/y2	q1/ y1	q2	q4
q2	q3/y3	---	q2/y1	q5	q2
q3	q4/y3	q2/y1	q3/y3	q5	q2
q4	---	q2/y2	q4/y2	q3	q1
	q5/y3	q3	q1

Граф автомата - ориентированный связный граф, вершины которого соответствуют состояниям, а дуги - переходам между ними. Две вершины графа автомата q_i и q_j (исходное состояние и состояние перехода) соединяются дугой, направленной от q_i к q_j, если в автомате есть переход q_i®q_j, т. е. если q_j=d(q_i, x_k) при некотором x_kÎX. В случае автомата Мили дуге графа приписываются входной символ x_k и выходной символ y_g=l(q_i, x_k), Если некоторые состояния автомата не определены, то в соответствующих клетках таблицы ставится прочерк; в этом случае автомат является частичным. Если переход q_i®q_j происходит под действием нескольких входных символов, то дуге (q_i, q_j) приписываются все эти входные и соответствующие выходные символы. При описании автомата Мура в виде графа выходной символ y_g=l(q_j) записывается рядом с вершиной q_j (или внутри неё).

На рис. 2.2 и 2.3 приведены заданные ранее табл. 2.1 и 2.2 графы автоматов А1 (частичный автомат Мили) и А2 (автомат Мура; здесь переход q₂®q₂ является петлёй).

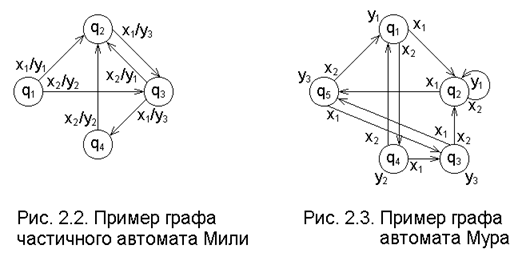Таблица 2.3

МТ	x0	...	xi	...	xn
q0	q0 x0 S	...	q0 xi S	...	q0 xn S
...	...	...	...	...	...
qj	q0 x0 L	...	qr xk S	...	qj xi R
...	...	...	...	...	...

Если функциональная схема МТ задана, то при каждом заполнении ленты работа машины однозначно определена.

Далее будем считать, что символ q₀ состояния УУ означает состояние покоя МТ, т. е. строка q₀ ФС обладает следующими свойствами:

· первым символом в каждой клетке этой строки всегда является q₀;

· вторым символом в клетке столбца x_i этой строки является символ x_i;

· третьим символом в каждой клетке строки является символ S.

Поэтому, если УУ в какой-то момент имеет состояние q₀, то где бы ни находилась головка и каким бы ни было заполнение ленты, в последуюший момент времени УУ будет оставаться в том же состоянии, заполнение ленты останется прежним, головка также не сдвинется. Для упрощения записи ФС строка q₀ в ней опускается.

В дальнейшем для простоты будем предполагать, что алфавит символов Х состоит из двух символов: "пустого" - 0 и "не пустого" - 1.

Рассмотрим несколько примеров МТ. Начальным состоянием машины здесь и далее будем считать состояние q₁; рассмотренные в этих примерах машины имеют по одному состоянию (не считая состояния покоя).

Пример 2.4. Машина А (табл. 2.4). Если в начальный момент машина воспринимает заполненную ячейку, то она "отыскивает" на ленте первую пустую (т.е. заполненную символом 0 ячейку) справа от той, над которой находится головка, вписывает туда символ 1 и останавливается. Если вначале головка находится напротив пустой ячейки, то машина её "заполняет" и останавливается, не передвигая головку.

Пример 2.5. Машина B (табл. 2.5) "стирает" единицу в той ячейке, над которой находится головка (если ячейка не пустая), передвигает головку влево и останавливается. Если в начальный момент ячейка под головкой пустая, то машина передвигает головку влево до тех пор, пока не найдёт заполненную ячейку, очищает её, передвигает головку влево и останавливается.

Пример 2.6. Машина С (табл. 2.6), отправляясь от заполненной ячейки, идёт влево и останавливается левее группы единиц на две ячейки.

Пример 2.7. Машина D (табл. 2.7), имея два состояния покоя, распознает, напротив какой ячейки находится, - пустой либо заполненной; в зависимости от этого переходит в первое либо второе состояние покоя.

В некоторых случаях МТ может быть недоопределена в том смысле, что не все ячейки её ФС заполнены. Это допускается в тех случаях, когда можно заранее сказать, что некоторые сочетания состояний машины и символов на ленте по тем или иным причинам никогда не встречаются.

Иногда МТ может иметь несколько состояний покоя: .

Таблица 2.4 Таблица 2.5 Таблица 2.6 Таблица 2.7

A

B

C

D

q1

q01S

q11R

q1

q10L

q00L

q1

q00L

q11L

q1

q0’0S

q0’’1S

Суперпозиция машин Тьюринга

Относительно МТ применимы такие соглашения:

· работа машины однозначно определена функционированием УУ в соответствии с её функциональной схемой;

· МТ всегда начинает работу от начального состояния (символ q₁) и имеет состояние покоя (символ q₀), которым заканчивается её работа.

Эти соглашения позволяют определить операции над МТ, благодаря которым можно по заданным ФС получать новые ФС. Различают следующие операции над машинами Тьюринга: композиция (произведение) и ите-рация, а также их комбинации, что позволяет строить суперпозиции МТ.

Пусть имеются две МТ: Т1 и Т2. Произведением МТ Т1 и Т2 называется машина Т, T=T₁T₂, ФС которой строится так:

· если УУ машин Т1 и Т2 имеют m₁ и m₂ состояний соответственно (исключая состояние покоя), то УУ машины Т имеет m₁+m₂ состояний, причём начальным состоянием машины Т является начальное состояние машины Т1 ( ), а конечным - состояние покоя машины Т2 ( ), т. е. машина Т1 начинает работу, затем передает «эстафету управления» машине Т2, а Т2 заканчивает её;

· ФС машины Т состоит из двух частей: верхняя описывает машину Т1, а нижняя - Т2, причём состояние покоя Т1 отождествляется с начальным состоянием Т2, т. е.

Операция умножения машин обладает свойствами:

1) Т1 Т2 ¹Т2 Т1 (некоммутативность);

2) ( Т1 Т2 ) Т3 = Т1 ( Т2 Т3 ) = Т1 Т2 Т3 (ассоциативность).

Возможен случай произведения одинаковых машин - степень МТ:

Тⁿ = ТТ...Т - n раз.

До сих пор рассматривалось умножение машин, имеющих одно состояние покоя. В том случае, когда одна из перемножаемых машин имеет несколько состояний покоя, умножение определяется аналогично описанному, но обязательно должно присутствовать указание, какое из состояний покоя предыдущего сомножителя отождествляется с начальным состоянием данного. Так, например, если машина Т1 имеет два состояния покоя, то произведение Т1 и Т2 может быть обозначено через

T=T₁ либо T=T₁ (2.13)

в зависимости от того, отождествляется ли начальное состояние машины Т2 с первым или со вторым состоянием покоя машины Т1. Машина Т в этом случае также имеет два состояния покоя: для первого варианта - состояние покоя машины Т2 либо второе состояние покоя машины Т1, для второго варианта - первое состояние покоя машины Т1 либо состояние покоя машины Т2.

Из предыдущего определения ясен также смысл такой, например, записи (формулы):

Т=T1 . (2.14)

Здесь умножение производится независимо по двум "каналам", которые связаны с первым либо вторым состоянием покоя машины Т1.

Рассмотрим операцию итерации, которая применяется к одной машине. Пусть машина Т1 имеет r состояний покоя. Выберем какое-либо l-е состояние покоя и отождествим его в ФС машины Т1 с начальным состоянием. Полученная машина является результатом итерации машины Т1 и обозначается через

Т= . (2.15)

Здесь точки над Т1 и l указывают на отождествление l-го состояния покоя машины Т1 с её начальным состоянием ( ). Отметим, что если Т1 имеет лишь одно состояние покоя, то после применения итерации получается машина, не имеющая вовсе состояния покоя.

Если обратиться к понятию ²программа² для МТ, то, как не трудно видеть, композиции машин соответствует линейное представление общей программы, итерации - циклическое представление, а множеству стоп-состояний – разветвление в программе. Таким образом, в программе (алгоритме, поскольку программа – одно из представлений алгоритма) для суперпозиции МТ можно выделить три базовых фрагмента, присущих схемам алгоритма. Из этого следует принципиальная возможность создания МТ (её ФС), реализующей любой алгоритм. Эта возможность утверждается в основной гипотезе теории алгоритмов: всякий алгоритм может быть задан посредством тьюринговой функциональной схемы и реализован в соответствующей машине Тьюринга.

Пример 2.7 Пусть имеются 4 машины (A, B, C и D), заданные своими ФС (табл. 2.4 - 2.7). Суперпозиция N из заданных МТ описывается формулой

(2.16)

Для суперпозиции N требуется построить: 1) функциональную схему; 2) схему алгоритма; 3) граф переходов, а также записать словесное описание работы машины N.

1. Составляем для машины N функциональную схему, заполняя её строками из ФС каждой исходной машины в том порядке, в каком они записаны в формуле (слева направо и сверху вниз); далее записываем состояния в первой колонке таблицы в порядке возрастания их номеров, обозначив состояния машины N pºq, и соответственно проводим переобозначение состояний в двух других колонках с учётом правил передачи ²эстафеты управления². В результате получаем табл. 2.8.

Таблица 2.8

C D B A	N			Список обозначений
p1	p20L	p11L
p2	p30S	p41S
p3	p30L	p10L
p4	p01S	p41R

2. По полученной ФС строим схему алгоритма, исходя из того, что каждая строка ФС может рассматриваться как условный оператор программы функционирования МТ, а состояние (имя строки) – как метки этой программы.

На рис. 2.5,а представлена СА функционирования машины N. Здесь SL(x) (SR(x)) – процедура SEARCH поиска на ленте символа x (X={0, 1}) при движении головки влево (вправо); R, L, S – команды на перемещение головки; Z - содержимое текущей ячейки. Для примера на рис. 2.5,б показана процедура SL(x).

3. В соответствии с табл. 2.8 строим граф переходов машины N (рис. 2.5,в), отмечая на переходах из состояния в состояние реакцию УУ (команды головке на запись символа в ячейке и на перемещение головки) в зависимости от символа, обозреваемого головкой на ленте.

На рис. 2.6 приведен пошаговый процесс обработки данных на ленте (подчёркнута ячейка, над которой находится головка в данном такте; жирным шрифтом отмечена цифра, которая изменилась на прошлом такте).

Такт Номер Ситуация на ленте

Состояния

0 1 …110100111100…

1 1 …110100111100…

2 1 …110100111100…

3 1 …110100111100…

4 1 …110100111100…

5 2 …110100111100…

6 3 …110100111100…

7 3 …110100111100…

8 1 …110000111100…

9 2 …110000111100…

10 4 …110000111100…

11 4 …110000111100…

12 0 …111000111100…

Рис. 2.6. Ситуации на ленте (к концу такта) при работе машины N

4. По СА функционирования (это можно сделать и по ФС) сформируем один из вариантов словесного описания алгоритмов функционирования машины N: машина, двигаясь влево, проходит группы пустых или заполненных ячеек, причём первую заполненную ячейку после группы пустых очищает, отыскивает на ленте одинокую пустую ячейку (ситуацию ...101...), заполняет её и останавливается над ней.

Отметим, что при отсутствии на ленте указанной ситуации головка дойдёт до левой границы ленты, что можно рассматривать как аварийное завершение работы машины.

Заключение

Рассмотрены 3 модели вычислений: ассоциативные исчисления (для логических вычислений), рекурсивные функции (для численных вычисле-ний) и машины Тьюринга (для общего случая вычислений, включая сим-вольную обработку). Последняя модель используется также для доказа-тельства существования алгоритма решения класса задач. Алгоритмы, соответствующие этим моделям, равносильны и могут быть получены друг из друга. Существуют и другие, специализированные модели.

Уточнение понятия ²алгоритм² основано на использовании тезиса Чёрча (классы ВФ и ОРФ равны) и на строгом определении двух объектов: 1) класс ОРФ; 2) МТ. В 1-м случае уточнение косвенное, во 2-м – прямое.

Исчисление – это не алгоритм, однако упорядочение допустимых подстановок, предложенное А.А. М