Методика обучения решению задач

Тема: Обучение решению простых задач на

Сложение и вычитание

План:

1. Роль задач в начальном курсе математики (записать ответ на вопрос в тетрадь для лекций).

2. Обучение решению простых задач:

а) раскрывающих смысл действий сложения и вычитания;

б) на увеличение (уменьшение) числа на несколько единиц;

в) на разностное сравнение;

г) с неизвестным слагаемым;

д) с неизвестным уменьшаемым;

е) с неизвестным вычитаемым.

3. Анализ видав задач с теоретико-множественной точки зрения.

Рекомендательная литература

1. Гребенникова Н.Л. Ознакомление первоклассников с задачей // Начальная школа. 1990. - №10. – С. 34-37.

2. Истомина Н.Б. Первые шаги в формировании умения решать задачи //Начальная школа. – 1981. - №11. – С. 40-42.

3. Царева С.Е. Приемы первичного анализа задачи // Начальная школа. – 1985. - №9. – С. 46-49.

4. Шмырева Г.Г. Предупреждение ошибок в выборе арифметического действия при обучении решению задач // Начальная школа. – 1985. - №10. – С. 37-39.

5.

В начальном курсе математики большую роль играют задачи. Они выполняют функцию не только самостоятельного объекта изучения, но и важного средства, с помощью которого младшие школьники осваивают математические понятия. В зависимости от количества действий, с помощью которых решается задача, различают задачи простые (в одно действие) и составные (в два и более действий) в начальных классах вводятся 25 видов только простых задач, каждый из которых имеет свои методические особенности. Поэтому решение обычно является «камнем преткновения» для младших школьников. В связи с этим, рассмотрим данный вопрос более подробно.

Что значит решить задачу? На этот вопрос отвечают, как правило, следующим образом: «Решить задачу – это значит найти правильный ответ». Но это не совсем так. решить задачу, это значит:

- разобраться в условии задачи, выделить входящие в нее величины, определить, какие из них известны, а какую надо найти;

- выяснить, как между собой эти величины связаны;

- на основе этого правильно выбрать арифметическое действие;

- записать соответствующий пример, вычислить его и записать ответ.

Как видим, решение задачи включает в себя следующие элементы: а) анализ условия задачи, выделение известных величин и той, которую надо найти; б) краткая запись условия задачи; в) разбор задачи, составление плана решения (в составных задачах); г) запись решения; д) проверка решения.

Виды задач в 1 классе

В 1 классе четырехлетней начальной школы дети знакомятся со следующими видами простых задач:

Вид задачи	Пример данного вида задачи
1. На нахождение суммы	У Саши было 6 тетрадей в клетку и 2 в линейку. Сколько всего тетрадей было у Саши?
2. На нахождение остатка	У Саши было 8 тетрадей. 2 тетради он сдал учителю. Сколько тетрадей у него осталось?
3. На увеличение числа на несколько единиц	У Саши было 6 тетрадей в клетку, а в линейку на 2 тетради больше. Сколько всего тетрадей было у Саши?
4. На уменьшение числа на несколько единиц	У Саши было 6 тетрадей в клетку, а в линейку на 2 тетради меньше. Сколько всего тетрадей было у Саши?

Задачи на нахождение суммы

Задачи на нахождение суммы раскрывают конкретный смысл действия сложения. Поэтому на подготовительном этапе работы над этим видом задачи необходимо постоянно оперировать с предметными множествами, делая упор на операцию объединения множеств. Приведем пример такой работы.

- Положи слева 5 красных кружочков, а справа – 3 синих кружочка. Придвинь синие кружочки к красным (при этом делается жест объединения синих кружочков с красными). Больше стало кружочков или меньше? (Больше.) Сколько всего стало кружочков? (8.) Каким действием это узнаем? (Сложением.)

В дальнейшем осуществляется переход предметных действий с кружочками к их моделям, которые вычерчиваются в тетради (размер кружочка – одна клеточка, интервал между ними тоже одна клеточка). В этом случае объединение множеств ребенок осуществляет мысленно и фиксирует это объединение на чертеже в виде стрелочки.

Для того, чтобы лучше разобраться в условии задачи, выделить входящие в нее величины, выполняется краткая запись условия, которая предшествует выбору арифметического действия и записи решения задачи. Для данного вида задач традиционной является следующая форма краткой записи условия (рассмотрим ее на примере приведенного выше текста задачи):

Пояснение обозначений: К. – тетрадей в клетку, Л. – тетрадей в линейку.

Однако величины, входящие в условие задачи, и отношения между ними более наглядно отображаются в краткой записи условия, которая выполнена в виде следующих схем:

а) схема в форме полоски:

б) схема в форме отрезка:

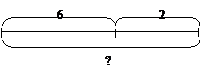
Использование таких схем больше помогает детям правильно выбрать нужное арифметическое действие для решения задачи.

Решение задачи на данном этапе записывают следующим образом:

6 + 2 = 7 (т.)

Ответ: 8 тетрадей.

Задачи на нахождение остатка

Данный вид задачи раскрывает конкретный смысл действия вычитания. Методика работы с такими задачами похожа на предыдущий вид, только вместо операции объединения множеств используется операция удаления части множества. Традиционная форма краткой записи условии выглядит так:

Задачи на увеличение и уменьшение числа на несколько единиц

В основе правильного решения этих видов задач лежит понимание смысла отношений «больше на», «меньше на». Так, например, если тетрадей в клетку – 6, а в линейку на 2 больше, то это значит, что в линейку столько же, сколько в клетку, и еще 2. на схеме это отношение оформляется так:

Проверочные задания по теме «Решение задач»

Реши задачи:

1) В одной тарелке 5 яблок, а в другой – 4 яблока. Сколько яблок в двух тарелках?

2) У Саши было 7 марок. 2 марки он подарил другу. Сколько марок осталось у Саши?

3) В одной вазе – 6 цветов, а в другой – на 2 больше. Сколько цветов во второй вазе?

4) В гараже было 8 легковых машин, а грузовых – на 3 меньше. Сколько грузовых машин было в гараже?

5) На столе лежат 5 ложек, а вилок на 2 больше, чем ложек. Сколько вилок лежат на столе?

6) Сшили 9 платьев, а блузок на 3 меньше, чем платьев. Сколько сшили блузок?

7) Антону 7 лет, а его сестре на 2 года меньше. Сколько лет сестре Антона?

8) К озеру идут 5 уток, а утят на 4 больше, чем уток. Сколько утят идут к озеру?

9) Феде 10 лет, а Петя моложе Феди на 3 года. Сколько лет Пете?

10) На берегу 7 пингвинов, а на льдине на 3 пингвина меньше. Сколько пингвинов на льдине?

Решение простых задач

Во 2 классе продолжают решать простые задачи. В дополнение к тем, которые были представлены в 1 классе, приведем еще несколько видов.

Вид задачи	Особенности работы над данным видом
На нахождение неизвестного слагаемого	Пример данного вида задачи: «В гараже было 5 грузовых и несколько легковых машин. Всего в гараже было 8 машин. Сколько легковых машин было в гараже?» Решение задач данного вида основывается на знании и умении применять следующее правило: «чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое». Однако опыт показывает, что дети не всегда осознанно используют это правило и решение данного вида задач часто усваивают формально. Для преодоления этой трудности могут оказать помощь следующие средства: 1) Построение моделей в виде отрезков. Построим модель для приведенной выше задачи: 2) Обращение к понятиям «часть» и «целое». В этом случае рассуждения ребенка по приведенной выше модели выглядят следующим образом: «Известно целое (8 м.) и часть (5 м.). чтобы найти часть, нужно из целого вычесть другую часть». 3) Одновременное решение задач на нахождение неизвестного слагаемого и задач на нахождение суммы, т.к. они являются взаимно обратными задачами.
На разностное сравнение	Различают два вида задач на разностное сравнение, которые отличаются друг от друга вопросом: 1) задачи с вопросом «на сколько больше?» (В гараже было 5 грузовых и 8 легковых машин. На сколько легковых машин было больше, чем грузовых?); 2) задачи с вопросом «на сколько меньше?» (В гараже было 5 грузовых и 8 легковых машин. На сколько грузовых машин в гараже было меньше, чем легковых?) Трудность состоит в том, что, несмотря на разные опорные слова в вопросах этих задач, обе они решаются действием вычитания. Дети же, ориентируясь на слово «больше», иногда для решения выбирают действие сложения. в установлении правильных отношений между величинами в задачах на разностное сравнение поможет «метод следов». Его суть состоит в следующем. На столе выкладывается в верхнем ряду 5 красных кружочков, а в нижнем ряду – 8 синих кружочков: затем кружочки убираются парами (по одному из каждого ряда) до тех пор, пока в верхнем ряду все кружочки не закончатся. В ходе этого процесса наглядно видно, почему задача решается действием вычитания: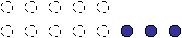