Тема: Методика изучения нумерации в концентре

«Тысяча»

План:

1. Цели обучения нумерации в пределах 1000.

2. Преемственность изучения нумерации чисел в концентре «Сотня» и «Тысяча» (сходство и различие).

3. Реализация задач темы на основе анализа фрагментов уроков.

- по ознакомлению с новой единицей «сотня».

- по ознакомлению с трехзначными числами.

4. Дидактические игры, способствующие закреплению различных вопросов нумерации.

Рекомендательная литература

1. Савина Л.П. Изучение чисел до 1000 // Начальная школа. – 1993. - №8. – С. 27-29.

Особенностью изучения нумерации чисел в концентре «Тысяча» является использование аналогии как основного метода, а в качестве часто используемого приёма – анализ готового выражения. Это объясняется тем, что учащиеся уже знакомы основными вопросами, изучаемые в концентрах «Десяток», «Сотня», выполняли соответствующие упражнения, а потому, смогут распространить свои умения на более широкий класс чисел.

В раздел, связанный с освоением нумерации трехзначных чисел, входит: изучение последовательности чисел в пределах 1000, их чтение и запись; знакомство с разрядом сотен, сотней как новой разрядной единицей; представление трехзначного числа в виде суммы разрядных слагаемых.

В целом методика изучения этой темы сходна с изучением нумерации двузначных чисел. Поэтому остановимся только на изучении записи трехзначных чисел. Для этого целесообразно использовать трехразрядный абак:

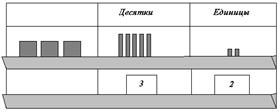
Для того, чтобы записать число 352, сначала построим его модель в верхнем ряду абака. В этой модели маленькие квадратики обозначают единицы, полоски – десятки (каждая полоска содержит 10 квадратиков), большие квадраты – сотни (каждый большой квадрат состоит из 100 маленьких или 10 полосок.) После этого проводится следующая беседа: «Сколько сотен в числе триста пятьдесят два?» (Три.) «Обозначим это цифрой» (в левый нижний кармашек вставляется карточка с цифрой три). «Сколько отдельных десятков?» (Пять.) (В средний кармашек вставляется цифра 5.) «Сколько в числе триста пятьдесят два отдельных единиц?» (Две.) (В правый нижний кармашек вставляется цифра 2.)

При изучении нумерации следует обратить внимание на формирование умения заменять любое трехзначное число суммой разрядных слагаемых:

583 = 500 + 80 + 3; 405 = 400 + 5; 620 = 600 + 20.

Более трудными являются случаи с числами, содержащими в записи нули. Так, иногда дети допускают следующие ошибки (во втором примере действие хотя и выполнено верно, но оно ошибочно представляет разрядный состав числа 600):

608 = 60 + 8 600 = 500 + 100.

Разрядный состав играет большую подготовительную роль в изучении арифметических действий над трехзначными числами.

Повторение нумерации в пределах 100 позволяет ознакомить детей и с нумерацией в пределах 1000. К этому этапу они уже усвоили образование со­тен, от. счета десятками перешли к счету сотнями, повторили и обобщили вывод о том, что десятками и сотнями считают так же, как простыми единицами. Уже на первом уроке дети узнали названия чисел, которые обра­зуются при счете сотен. На основе знания со­става двузначных чисел из десятков и еди­ниц дети легко перешли к усвоению состава трехзначных чисел (2 д. 3 ед.=23, 1 с. 2 д. 3 ед.= 123). Работа с таблицей разрядов, с индивидуальными счетными книжками по­могает учащимся усвоить письменную ну­мерацию трехзначных чисел и понятие раз­ряда (единицы - единицы I разряда, десятки - единицы II разряда, сотни - единицы Ш разряда).

Повторение устных приемов сложения и вычитания в пределах 100 облегчит детям усвоить соответствующие приемы в пределах 1000:

50+7 89 – 9

500+70 890—90

36+3 80—3

360+30 800—30

Учащиеся не испытывают особой трудности при выполнении этих заданий, а повторение поможет им , используя аналогию, закрепление знаний, получить новое. Затем так же одновременно рассматриваются письменные приемы сложения и вычитания двузначных и трехзначных чисел:

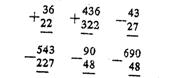
Одновременная работа над навыками устных и письменных вычислений в пределах 100 и 1000 развивает мышление учащихся, заставляет сравнивать, обобщать, повышает интерес к предмету. Более подготовленные ученики делают попытки перенести приобретенные навыки на многозначные числа, когда предлагают им самим составить примеры с любыми числами в которых, наряду с двухзначными числами, использованы и трехзначные. Например:

Х+17= 40 62 – 30… 62 – 40

или или

Х+170=400 620-300… 620- 400

Изучение сложения и вычитания двухзначных и трехзначных чисел, естественно, несколько отодвинуло изучение умножения и деления, но в то же время знание чисел, до 1000 расширило область применения таблицы умножения и деления, когда мы приступили к ее изучению.

Учащимся предлагаются такие примеры:

2 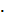4=8 2д 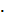4=8 д.=80

18:3=6 18д.:3=6д.=60

2с. 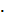4=8с.=800

18с.:3=6с.=600