Тема: Изучение нумерации чисел первого десятка

В начальных классах»

Стерлитамак 2010

УДК 372.8:51(0.7)
ББК 74 262.21
М54

Организация самостоятельной работы студентов по изучению курса «Методика преподавания математики в начальных классах»для студентов 3—5-х курсов заочного отделения по специальности “031200 — Педагогика и методика начального образования” / Сост. Р..3. Мустафина. Стерлитамак. Стерлитамак. гос, пед. академия им. Зайнаб Биишева, 2010. - 120 с.

Пособие представляет собой изложенную в сжатой форме систему подготовки по методике преподавания математики учителей начальных классов, а также приведены наиболее важные с методической точки зрения статьи. Задания, выполняемые ими по изучению начального курса математики (задания и вопросы к практическим и лабораторным занятиям, задания кконтрольным работам, вопросы к экзамену по методике математики, задания исследовательского характера к педагогическим практикам на 4 и 5-м курсах, вопросы к занятиям слецкурса), собраны воедино, образуя целостную картину подготовки будущего учителя начальных классов.

© Составитель: Р.З. Мустафина,
2010
© Стерлитамакская
государственная
педагогическая
академия им. Зайнаб Биишевой, 2010.

ВВЕДЕНИЕ

Основная цель пособия к изучению курса “Методика преподавания математики в начальных классах” — оказание помощи в подготовке студентов дневного и заочного отделений к экзамену, к выполнению контрольных работ, выбору темы, направления исследования при написании курсовой и дипломной работы, заданий к педагогической практике.

Пособие состоит из 5 частей:

Введение.

§ 1. Содержание лекций и практических занятий.

§ 2. Задания к выполнению контрольных работ.

§ 3. Задания к педагогической практике.

§ 4. Вопросы к экзамену.

§ 5. Темы курсовых работ.

В конце приводится список основной литературы, используемый при обучении.

В работе реализуется идея интеграции содержания и методов таких дисциплин, как педагогика (раздел дидактики), математика (конкретный смысл арифметических действий и их свойства, вопросы изучения величин и действий с ними, понятие разряда, класса, числа и др.) методика преподавания математики. Осознанное применение общедидактических закономерностей и знаний по вузовскому курсу математики к обучению математике младших школьников, а также мобильность современного учителя в умении анализировать новые подходы в обучении, являются действенным фактором совершенствования профессиональной подготовки будущего учителя. К практическим занятиям предлагаются задания, нацели- / вающие на установление межпредметных связей между названными дисциплинами. За период обучения методике преподавания математики и параллельно за время прохождения педпрактики в качестве учителя начальных классов у каждого. студента будет накоплен материал, куда войдет тематическое планирование, конспекты уроков, фрагменты уроков по отдельным трудным вопросам, методические разработки внеклассных мероприятий, набор дидактических игр, образцы и описание наглядных пособий, конспекты необходимых статей. Тогда каждый студент за годы изучения названного курса подготовит так называемую копилку” для работы с учащимися начальных классов.

К каждой теме указана литература, дополняющая учебники. В том числе предлагаются статьи 1970-80-х годов издания, которые в теоретическом и методическом плане важнее статей последних лет — их студенты могут подобрать самостоятельно, а также воспользоваться имеющимися в кабинете списками литературы к изучаемому курсу.

Содержание лекций и практических занятий

НУМЕРАЦИЯ ЦЕЛЫХ НЕОТРИЦАТЕЛЬНЫХ ЧИСЕЛ (6 часов)

Тема: Методика изучения нумерации

В концентре «Сотня»

План:

1. Задачи и структура темы.

2. Последовательность изучения темы:

а) Числа 11-20.. реализация задач изучения темы на следующих уроках:

- урок ознакомления с новой счетной единицей – десятком;

- уроки устной нумерации

- уроки письменной нумерации.

б) Числа 21-100. Поурочная характеристика реализации основных задач по учебнику математики М-2.

Выполнить задание:

Сделать анализ использования следующих средств наглядности:

- «лента ста»;

- полоски с кружками;

- карточки с разрядными числами.

г) Изучение дидактических игр к теме: Дрозд В.Л. и др. Практикум по методике начального обучения математике: Минский Е.М. От игры к знаниям. – М.: Просвещение, 1982.; Дышинский Е.А. Игротека математического кружка. – М.: Просвещение, 1972.

Нумерация чисел второго десятка (от 11 до 20)

В начале четвертой учебной четверти первоклассники знакомятся с числами второго десятка. В ходе изучения этой темы они усваивают последовательность натуральных числе в пределах 20, учатся читать, записывать и сравнивать эти числа (с использованием знаков «>», «<» и «=»), а также рассматривают десятичный состав двузначных чисел. рассмотрим методику работы над этими вопросами более подробно.

Изучая данную тему, важно показать ребенку процесс образования новой разрядной единицы – десятка. Для этого используются счетные палочки. Отсчитав вместе с ребенком десять палочек, их связывают в пучок и получают новую разрядную единицу - десяток. (Следует отметить, что «десять» и «десяток» - разные понятия. Если «десять» - это десять отдельных единиц, то «десяток» - это десять единиц, объединенных вместе, образующих новую счетную единицу.) Добавляя к десятку отдельные палочки (единицы), получают все остальные числа от 11 до 20. число 20 состоит из двух пучков палочек - десятков.

При знакомстве ребенка с записью и чтением чисел от 11 до 20 хорошую помощь оказывает специальное наглядное пособие – абак:

Сначала счетные палочки по одной кладут в правый верхний кармашек абака, сопровождая этот процесс счетом. Получив десять палочек, их связывают в пучок (десяток) и перекладывают из правого кармашка в левый. В правый кармашек добавляют еще несколько палочек. Дойдя до числа пятнадцать, ребенку задают следующие вопросы:

- Сколько десятков в числе пятнадцать? (Один.) Обозначим это цифрой (внизу на абаке ставится разрезная карточка с цифрой 1).

- Сколько отдельных (т.е. не объединенных в десяток) единиц в числе пятнадцать? (Пять.) Обозначим это цифрой (под пятью палочками ставится цифра 5).

Аналогично ведется работа над записью и чтением остальных чисел второго десятка. При этом следует обратить внимание на объединение значения каждой цифры в записи числа: когда она обозначает количество единиц, а когда – десятков. Тем самым у ребенка формируется понимание позиционной записи двузначных чисел.

Сравнение двузначных чисел

При сравнении натуральных чисел в пределах 20 ребенок может уже самостоятельно использовать второй прием сравнения, основанный не на соотнесении соответствующих предметных множеств, а на взаимном расположении сравниваемых чисел в числовом ряду. Его рассуждения могут выглядеть так: «Шестнадцать больше четырнадцати, так как шестнадцать в ряду чисел находится правее, чем четырнадцать».

На этом этапе дети уже начинают при сравнении чисел использовать знаки «>, «<» и «=».

Предложив ребенку несколько заданий на сравнение однозначных чисел с двузначными, желательно так потом построить с ним обсуждение этой работы, чтобы он самостоятельно «открыл» следующую закономерность: любое однозначное число меньше любого двузначного числа.

Сложение и вычитание чисел вида 10 + 8, 18 – 10, 18 – 8

Уже при изучении нумерации чисел второго десятка первоклассники могут научиться выполнять простейшие случаи сложения и вычитания, основанные на разрядном составе двузначных чисел. Так, например, выполняя вычитание чисел вида 18 – 10, ребенок сопровождает его следующим комментарием: «Восемнадцать – это десять и восемь. Если из восемнадцати вычесть десять, то останется восемь». Аналогично проводятся рассуждения для случая 18 – 8. На первоклассном этапе решение таких примеров желательно сопровождать соответствующими предметными действиями, например, со счетными палочками.

Таким образом, заканчивая 1 класс, ребенок должен достаточно хорошо ориентироваться в следующих вопросах раздела «Нумерация целых неотрицательных чисел»: знать последовательность чисел в пределах 20 как в прямом, так и в обратном порядке, место каждого числа в натуральном ряду; уметь для каждого числа называть предыдущее и непосредственно следующее за ним число, продолжать счет как в прямом, так и в обратном порядке от любого заданного числа в этих пределах; понимать, как образуется каждое число путем прибавления единицы к предыдущему числу и вычитания единицы из последующего числа натурального ряда; читать, записывать и сравнивать любые числа в пределах 20, записывать результат сравнения с помощью знаков «>, «<» и «=»; до автоматизма знать состав чисел в пределах десяти, а также разрядный состав (из десятков и единиц) двузначных чисел второго десятка. В качестве опережения требований программы 1 класса можно с ребенком хорошо отработать знание состава всех чисел в пределах 18 из двух однозначных слагаемых (например, 14 = 7 + 7, 14 = 6 + 8, 14 = 5 + 9).

С целью контроля за усвоением этих вопросов ребенку можно предложить следующие задания.

Проверочные задания по темам

«Числа от 1 до 10» и «Числа от 11 до 20»

1) Посчитай от 1 до 20 сначала в прямом, а затем в обратном порядке.

2) Посчитай от 8 до 20 в прямом порядке, от 14 до 1 в обратном порядке.

3) Вставь пропущенные числа в ряду:

а) 1, 2, …, 4, 6, 7, …, …, 10, …, …, …, 14, …, …, …, 19 …

б) … 18, …, …, …, …, …, …, …, 10, …, 8, …, …, …, 4, …, …, 1.

4) Используя карточки с разрезными цифрами, попросите ребенка построить из них в «Кассе счетного материала» отрезок натурального ряда от 1 до 10. предложите ему отвернуться, а сами в это время переставьте между собой местами два каких-либо числа. Задача ребенка – найти перестановку и восстановить исходный ряд.

5) Поставьте нужные знаки >, < или =:

8 … 6; 11 … 17; 8 … 13;

4 … 9; 20 … 18; 14 … 5;

7 … 7; 13 … 10; 20 … 10;

0 … 5; 15 … 15; 9 … 11;

6) Замени каждое число суммой десятка и единиц по образцу:

12 = 10 + 2; 17 = … + …; 14 = … + …;

15 = … + …; 18 = … + …; 10 = … + …;

7) Заполни таблицы состава следующих чисел:

Нумерация чисел от 21 до 100

Во 2 классе дети продолжают знакомство с двузначными числами в пределах от 21 до 100. эта тема изучается аналогично нумерации чисел от 11 до 20. вместе с тем, существует важная особенность, которая является причиной раздельного изучения этих двух числовых областей: если числа от 21 до 100 пишутся и читаются в одном и том же порядке, сначала десятки, потом - единицы, то во втором десятке читаются сначала единицы, а затем – десятки, в то время как запись числа осуществляется в обратном порядке. Ребенок сначала знакомится с разрядными числами («круглыми» десятками) – 20, 30, 40, 50, 60, 70, 80, 90, 100, - а затем со всеми остальными числами в пределах ста. При этом целесообразно использовать уже описанное выше наглядное пособие – абак:

При изучении чисел от 21 до 100 необходимо обратить особое внимание на чтение чисел 40 и 90, которое отличается от чтения остальных разрядных чисел.

Проверочные задания по теме

«Нумерация чисел от 21 до 100»

1) Назови числа по порядку: а) от 17 до 31; б) от 79 до 93; в) от 82 до 58.

2) Запиши числа по порядку: а) от 28 до 43; б) от 65 до 37.

3) Назови числа, которые предшествуют числам: 57, 81, 40.

4) Назови числа, которые следуют за числами: 34, 68, 70, 59, 99.

5) Назови «соседей числа: 42, 79, 50, 81.

6) Замени следующие числа суммой разрядных слагаемых: 35, 68, 70.

7) Сравни числа: 35 … 38; 57 … 27; 49 … 61; 90 … 53.

8) Сравни двузначные числа, в которых некоторые цифры заменены буквами (одинаковым цифрам соответствуют одинаковые буквы, знак 0 обозначает цифру «нуль»):

257 … 72; ж0 … ж7; ж5 … д5;

42 … 40; 3д … 4ж; жд …дж.

Сложение и вычитание

План:

1. Роль задач в начальном курсе математики (записать ответ на вопрос в тетрадь для лекций).

2. Обучение решению простых задач:

а) раскрывающих смысл действий сложения и вычитания;

б) на увеличение (уменьшение) числа на несколько единиц;

в) на разностное сравнение;

г) с неизвестным слагаемым;

д) с неизвестным уменьшаемым;

е) с неизвестным вычитаемым.

3. Анализ видав задач с теоретико-множественной точки зрения.

Рекомендательная литература

1. Гребенникова Н.Л. Ознакомление первоклассников с задачей // Начальная школа. 1990. - №10. – С. 34-37.

2. Истомина Н.Б. Первые шаги в формировании умения решать задачи //Начальная школа. – 1981. - №11. – С. 40-42.

3. Царева С.Е. Приемы первичного анализа задачи // Начальная школа. – 1985. - №9. – С. 46-49.

4. Шмырева Г.Г. Предупреждение ошибок в выборе арифметического действия при обучении решению задач // Начальная школа. – 1985. - №10. – С. 37-39.

5.

В начальном курсе математики большую роль играют задачи. Они выполняют функцию не только самостоятельного объекта изучения, но и важного средства, с помощью которого младшие школьники осваивают математические понятия. В зависимости от количества действий, с помощью которых решается задача, различают задачи простые (в одно действие) и составные (в два и более действий) в начальных классах вводятся 25 видов только простых задач, каждый из которых имеет свои методические особенности. Поэтому решение обычно является «камнем преткновения» для младших школьников. В связи с этим, рассмотрим данный вопрос более подробно.

Что значит решить задачу? На этот вопрос отвечают, как правило, следующим образом: «Решить задачу – это значит найти правильный ответ». Но это не совсем так. решить задачу, это значит:

- разобраться в условии задачи, выделить входящие в нее величины, определить, какие из них известны, а какую надо найти;

- выяснить, как между собой эти величины связаны;

- на основе этого правильно выбрать арифметическое действие;

- записать соответствующий пример, вычислить его и записать ответ.

Как видим, решение задачи включает в себя следующие элементы: а) анализ условия задачи, выделение известных величин и той, которую надо найти; б) краткая запись условия задачи; в) разбор задачи, составление плана решения (в составных задачах); г) запись решения; д) проверка решения.

Виды задач в 1 классе

В 1 классе четырехлетней начальной школы дети знакомятся со следующими видами простых задач:

Вид задачи	Пример данного вида задачи
1. На нахождение суммы	У Саши было 6 тетрадей в клетку и 2 в линейку. Сколько всего тетрадей было у Саши?
2. На нахождение остатка	У Саши было 8 тетрадей. 2 тетради он сдал учителю. Сколько тетрадей у него осталось?
3. На увеличение числа на несколько единиц	У Саши было 6 тетрадей в клетку, а в линейку на 2 тетради больше. Сколько всего тетрадей было у Саши?
4. На уменьшение числа на несколько единиц	У Саши было 6 тетрадей в клетку, а в линейку на 2 тетради меньше. Сколько всего тетрадей было у Саши?

Задачи на нахождение суммы

Задачи на нахождение суммы раскрывают конкретный смысл действия сложения. Поэтому на подготовительном этапе работы над этим видом задачи необходимо постоянно оперировать с предметными множествами, делая упор на операцию объединения множеств. Приведем пример такой работы.

- Положи слева 5 красных кружочков, а справа – 3 синих кружочка. Придвинь синие кружочки к красным (при этом делается жест объединения синих кружочков с красными). Больше стало кружочков или меньше? (Больше.) Сколько всего стало кружочков? (8.) Каким действием это узнаем? (Сложением.)

В дальнейшем осуществляется переход предметных действий с кружочками к их моделям, которые вычерчиваются в тетради (размер кружочка – одна клеточка, интервал между ними тоже одна клеточка). В этом случае объединение множеств ребенок осуществляет мысленно и фиксирует это объединение на чертеже в виде стрелочки.

Для того, чтобы лучше разобраться в условии задачи, выделить входящие в нее величины, выполняется краткая запись условия, которая предшествует выбору арифметического действия и записи решения задачи. Для данного вида задач традиционной является следующая форма краткой записи условия (рассмотрим ее на примере приведенного выше текста задачи):

Пояснение обозначений: К. – тетрадей в клетку, Л. – тетрадей в линейку.

Однако величины, входящие в условие задачи, и отношения между ними более наглядно отображаются в краткой записи условия, которая выполнена в виде следующих схем:

а) схема в форме полоски:

б) схема в форме отрезка:

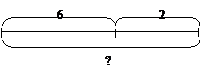
Использование таких схем больше помогает детям правильно выбрать нужное арифметическое действие для решения задачи.

Решение задачи на данном этапе записывают следующим образом:

6 + 2 = 7 (т.)

Ответ: 8 тетрадей.

Задачи на нахождение остатка

Данный вид задачи раскрывает конкретный смысл действия вычитания. Методика работы с такими задачами похожа на предыдущий вид, только вместо операции объединения множеств используется операция удаления части множества. Традиционная форма краткой записи условии выглядит так:

Задачи на увеличение и уменьшение числа на несколько единиц

В основе правильного решения этих видов задач лежит понимание смысла отношений «больше на», «меньше на». Так, например, если тетрадей в клетку – 6, а в линейку на 2 больше, то это значит, что в линейку столько же, сколько в клетку, и еще 2. на схеме это отношение оформляется так:

Проверочные задания по теме «Решение задач»

Реши задачи:

1) В одной тарелке 5 яблок, а в другой – 4 яблока. Сколько яблок в двух тарелках?

2) У Саши было 7 марок. 2 марки он подарил другу. Сколько марок осталось у Саши?

3) В одной вазе – 6 цветов, а в другой – на 2 больше. Сколько цветов во второй вазе?

4) В гараже было 8 легковых машин, а грузовых – на 3 меньше. Сколько грузовых машин было в гараже?

5) На столе лежат 5 ложек, а вилок на 2 больше, чем ложек. Сколько вилок лежат на столе?

6) Сшили 9 платьев, а блузок на 3 меньше, чем платьев. Сколько сшили блузок?

7) Антону 7 лет, а его сестре на 2 года меньше. Сколько лет сестре Антона?

8) К озеру идут 5 уток, а утят на 4 больше, чем уток. Сколько утят идут к озеру?

9) Феде 10 лет, а Петя моложе Феди на 3 года. Сколько лет Пете?

10) На берегу 7 пингвинов, а на льдине на 3 пингвина меньше. Сколько пингвинов на льдине?

Решение простых задач

Во 2 классе продолжают решать простые задачи. В дополнение к тем, которые были представлены в 1 классе, приведем еще несколько видов.

Вид задачи	Особенности работы над данным видом
На нахождение неизвестного слагаемого	Пример данного вида задачи: «В гараже было 5 грузовых и несколько легковых машин. Всего в гараже было 8 машин. Сколько легковых машин было в гараже?» Решение задач данного вида основывается на знании и умении применять следующее правило: «чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое». Однако опыт показывает, что дети не всегда осознанно используют это правило и решение данного вида задач часто усваивают формально. Для преодоления этой трудности могут оказать помощь следующие средства: 1) Построение моделей в виде отрезков. Построим модель для приведенной выше задачи: 2) Обращение к понятиям «часть» и «целое». В этом случае рассуждения ребенка по приведенной выше модели выглядят следующим образом: «Известно целое (8 м.) и часть (5 м.). чтобы найти часть, нужно из целого вычесть другую часть». 3) Одновременное решение задач на нахождение неизвестного слагаемого и задач на нахождение суммы, т.к. они являются взаимно обратными задачами.
На разностное сравнение	Различают два вида задач на разностное сравнение, которые отличаются друг от друга вопросом: 1) задачи с вопросом «на сколько больше?» (В гараже было 5 грузовых и 8 легковых машин. На сколько легковых машин было больше, чем грузовых?); 2) задачи с вопросом «на сколько меньше?» (В гараже было 5 грузовых и 8 легковых машин. На сколько грузовых машин в гараже было меньше, чем легковых?) Трудность состоит в том, что, несмотря на разные опорные слова в вопросах этих задач, обе они решаются действием вычитания. Дети же, ориентируясь на слово «больше», иногда для решения выбирают действие сложения. в установлении правильных отношений между величинами в задачах на разностное сравнение поможет «метод следов». Его суть состоит в следующем. На столе выкладывается в верхнем ряду 5 красных кружочков, а в нижнем ряду – 8 синих кружочков: затем кружочки убираются парами (по одному из каждого ряда) до тех пор, пока в верхнем ряду все кружочки не закончатся. В ходе этого процесса наглядно видно, почему задача решается действием вычитания: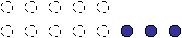

Уnpажнения.

1. Объясните смысл предложения:

а) самолет летит со скоростью 950 км/ч;

б) улитка ползет со скоростью 6 м/ч;

в) плот плывет по реке со скоростью 4 км/ч;

г) человек идет со скоростью 5 км/ч.

2. Назовите скорость, с которой может идти пешеход, автобус, такси, электропоезд, лететь самолет.

3. Чему равна скорость движения:

а) меч-рыбы, если она в каждый час про­плывает 100 км?

б) пчелы, если она в каждую секунду пролетает 7 м?

в) верблюда, если он в каждый час про­ходит 35 км?

г) космического корабля, если он в каждую секунду пролетает 8 км?

д) велосипедиста, если он в каждый час проезжает 18 км?

4. Вы знаете, что для определения мас­сы используют прибор, который называют весы, для измерения длины используют ли­нейку или рулетку, для измерения време­ни - часы. А каким прибором измеряют скорость?

Для измерения скорости используют при­бор, который называют спидометром (от англ. speed - скорость). По показаниям спи­дометра узнайте и запишите скорость дви­жения каждой машины:

5. За 6 ч, двигаясь без остановок, поезд прошел 498 км. Сколько километров прохо­дил поезд в каждый час? С какой ско­ростью шел поезд?

6. Один велосипедист за 2 ч проехал 24 км, а другой за то же время - 26 км. Найдите скорость каждого велосипедиста. Скорость какого велосипедиста больше? Что значит скорость больше?

7. За 1 ч автомобиль прошел 60 км. Сколько километров он проходил в каждую минуту? Запишите скорость автомобиля, ис­пользуя единицу скорости км/мин.

8. Я заметил в бинокль предмет, дви­жущийся со скоростью 1000 м/мин. Вырази­те эту скорость в км/мин.

В течение следующих 3-4 уроков по из­вестной учителю методике учащиеся решают задачи на определение пути по данным ско­рости и времени движения и на опреде­ление времени по двум другим известным величинам - пути и скорости.

После рассмотрения решения, каждой из этих задач полезно вслух проroворить. выво­ды: 1) чтобы найти длину пути, надо вре­мя умножить на скорость; 2) чтобы найти время, надо длину пути разделитъ на ско­рость.

При решении задач на движение в сред­них классах учащиеся встречаются с боль­шими трудностями - переводом скорости, данных в одних единицах, в другие еди­ницы. Дело не в том, что соответствую­щее умение трудно сформировать. Этим надо специально заниматься, а в программе по ма­тематике для начальной школы этому вопро­су не уделяется внимания и нужных видов упражнений в учебнике математики, есте­ственно, нет. А определенную работу в этом направлении можно провести уже в началь­ных классах.

Предлагаем для тренировки несколько видов таких упражнений. Эти упражнения помогут научить учащихся переводить одни единицы в другие и будут способствовать развитию их мышления.

Упражнения.

1. Космический корабль летит со скоро­стью 8 км/с. Сколько километров он про­летит за 1 мин? Запишите скорость ко­рабля в км/мин.

2. Машина прошла 150 км за 2 ч 30 мин. Найдите скорость машины и запишите ее в км/ч.

3. Велосипедист едет по дороге со скоро­стью 15 км/ч. Какое расстояние он проедет за 20 мин?

Решение. Покажем наиболее простой способ рассуждения. В 1 ч содержится 3 раза по 20 мин (60:20=3). Значит, 20 мин – это 1/3 часа. Так как каждый час велосипедист проезжает 15 км, то за 3 часа он проедет 5 км (15:3=5). Ответ. 5 км.

4. Человек идет по дороге со скоростью 4 км/ч. За какое время он пройдет 3 км?

Решение. По условию задачи человек проходит 4 км за 60 мин. Значит, 1 км он проходит за 15 мин (60:4= 15), а 3 км он пройдет за 45 мин (15*3=45).

Ответ. За 45 мин.

5. Стрекоза летит со скоростью 10 м/с. Сколько километров она пролетит за 1 ч?

Решение. В 1 ч содержится 3 600 с (60·60=3600). По условию задачи за 1 с стрекоза пролетает 10 м, а за час, т. е. за 3 600 с она пролетит в 3 600 раз большее расстояние, т. е. 10·3600=36000=36 кило­метров.

Ответ. 36 км.

При обучении решению задач на дви­жение двух тел в противоположных направ­лениях для предупреждения механического запоминания некоторыми учениками способа решения задачи полезно предлагать зада­чи, по сюжету и способу решения знако­мые учащимся, но числовые данные подби­рать так, чтобы формальный, заученный спо­соб решения, примененный к таким задачам, привел бы учеников к ошибке или поставил их в тупик и они вынуждены были ду­мать, рассуждать, искать правильное реше­ние.

Примеры таких задач.

1. Два пешехода вышли одновременно на­встречу друг другу из двух деревень. Ско­рость одного пешехода 5 км/ч, а другого 4 км/ч. Расстояние между деревнями 3 км. Какое расстояние будет между пешеходами через час после начала движения?

Решение. Через час от начала движе­ния пешеход, идущий со скоростью 5 км/ч, пройдет 5 км. За это время он дойдет до деревни (до нее 3 км) и пройдет дальше еще 2 км. Второй пешеход за час дойдет до деревни (3 км) и пройдет еще 1 км. Значит, через час от начала движе­ния расстояние между пешеходами будет 6 км (3+2+1=6).

Ответ. 6 км.

2. Из села в город на велосипеде выехал почтальон со скоростью 12 км/ч. В то же время навстречу ему из города в село вы­шел турист со скоростью 6 км/ч. Расстоя­ние от села до города 9 км. Какое рас­стояние будет между ними через полчаса?

Решение. За полчаса почтальон проедет 6 км (12:2= 6), а турист пройдет 3 км (6:2=3). Так как расстояние от села до города 9 км, то через полчаса после нача­ла движения почтальон, пройдя 6 км, а ту­рист 3 км, встретятся (6+3=9). В момент встречи расстояние между ними будет0.

О т в е т. Расстояние равно 0.

IV. Проверка решения

Цель: установить, соответствует ли процесс и результат решения образцу правильного решения.

Приемы выполнения:

1. Прогнозирование результата (прикид­ка, установление границ ответа на вопрос за­дачи) и последующее сравнение хода реше­ния с прогнозом. При несоответствии прогнозу — решение неверно. При соответствии решение может быть как верным, так и не­ верным. (Возможно установление правильности (правдоподобности) или неправильности (неправдоподобности) хода решения.)

2. Установление соответствия между результатом решения и условием задачи: введение в текст задачи вместо вопроса (требования) ответа на него (утверждение о выполнении требования), получение всех возможных следствий из полученного тек­ста, сопоставление результатов друг с другом и с информацией, содержащейся в тексте. (Если в результате будут обнаружены противоречивые утверждения, то зада­ча решена неправильно. В противном случае — результат решения верен. Правиль­ность хода решения не устанавливается.)

3. Решение другим методом или спосо­бом. (Если в результате решения другим, (другими) способом или методом получили тот же результат - этот результат верен, в противном случае - неверен. Правиль­ность хода решения не устанавливается.)

4. Составление и решение обратной за­дачи. (Если в результате решения обратной задачи получено данное прямой задачи, то результат решения - верен. В противном слу­чае - неверен. Правильность хода решения не устанавливается.)

5. Определение смысла составленных в процессе решения выражений. (Если все выражения имеют смысл и смысл последне­го таков, что позволяет ответить на вопрос задачи, то выражения составлены верно и после проверки правильности нахождения значений выражений можно утверждать, что ход и результат решения верны. В про­тивном случае либо ход решения, либо его результат - неверны. Возможно установле­ние правильности как хода, так и результа­та решения.)

6. Сравнение с правильным решени­ем - с образцом хода и (или) результата решения. (При решении задачи тем же ме­тодом и способом, что и в имеющемся об­разце, возможно установление правильно­сти как хода, так и результата решения.)

7. Повторное решение тем же методом и способом. (Возможно установление пра­вильности хода и результата решения.)

8. Решение задач "с малыми числами" с последующей проверкой вычислений. (Возможно установление правильности хо­да и результата решения.)

9. Решение задач с упрощенными отно­шениями и зависимостями с последующим восстановлением отношений и зависимос­тей, данных в задаче. (Возможно установление правильности как хода, так и резуль­тата решения.)

10. Обоснование (по ходу) каждого ша­га решения через соотнесение с более об­щими теоретическими положениями. (Воз­можно установление правильности как хо­да, так и результата решения.)

V. Формулировка ответа на вопрос задачи (вывода о выполнении требования).

Цель: дать ответ на вопрос задачи (подтвердить факт выполнения требования задачи).

Формы и способы выполнения:

1. Построение развернутого истинного суждения вида: "Так как..., то можно сделать вывод, что... (формулируется ответ на вопрос задачи полным предложением в устной или письменной форме).

2. Формулировка полного ответа на во­прос задачи без обосновывающей частиустно или письменно.

3. Формулировка краткого ответа устно или письменно с помощью специальных знаков.

VI. Исследование решения.

Цель: установить, является ли данное решение (результат решения) единствен­ным или возможны и другие результаты (ответы на вопрос задачи), удовлетворяющие условию задачи.

Приемы выполнения:

1. Изменение результата решения в со­ответствии с его смыслом и установление характера (направления) изменений в от­ношениях между измененным результатом и условием задачи.

Подбор другого результата решения и установление соответствия (возможнос­ти соответствия) условию задачи. Оценка степени возможности удовлетворения условию задачи других результатов.

Итак, чтобы решить задачу, нужно вна­чале ознакомиться с ней и понять ее, затем составить план решения, после чего выпол­нить его, сформулировать ответ на вопрос (вывод о выполнении требования) задачи, проверить ход и результат решения; выяс­нить, возможны ли другие результаты ре­шения. Выполнить каждый из перечислен­ных этапов можно, применив один или не­сколько приемов, названных выше или сконструированных на их основе самосто­ятельно.

Часть из перечисленных выше приемов универсальна, т.е. применима к любым за­дачам, другая часть применима лишь к ма­тематическим задачам. Существуют и при­емы более узкого назначения - для задач определенного вида. Выбор данного выше набора приемов обусловлен прежде всего результативностью и конструктивностью, т.е. возможностью расчленения на вполне конкретные и доступные освоению детьми операции.

Выделенные приемы, ис­пользуются явно или неявно в опыте, часть из них представлена в описаниях процессов решения задач.

Представленные элементы теории решения задач, их смыс­лы, содержательное наполнение составля­ют содержание обучения решению задач и соответствующий взгляд на проблему обучения этому содержа­нию.

Ход урока

Актуализация знаний.

1. Устно. Я называю число, а тот, кого спрошу, с него продолжает счет:

5 (6, 7, 8, 9, 10)

3 (4, 5, 6, 7, …)

А теперь в обратном порядке:

7 (6, 5, 4, 3, 2, 1)

4 (3, 2, 1)

9 (8, 7, 6, 5, 4, 3, 2, 1)

- Как удобно считать – в прямом или обратном порядке? (в прямом)

- Почему? ( мы так привыкли)

- С какого числа мы начинаем счет? (с числа 1)

- Возьмите в руки полоски бумаги, образуйте с их помощью цифру 1 и покажите. (Дети берут по 2, 3 палочки, показывают).

- Если не догадываются, я их прошу:

- А сможете показать цифру 1, используя только одну палочку? (Да, надо ее согнуть).

- Какая сначала была полоска? (ровная, прямая)

- А какая стала? (кривая)

II Объяснение нового. 1. На доске с двух сторон начерчены прямые и непрямые линии:

- Что начерчено на доске? (разные линии)

- А почему – в разных местах? Чем они отличаются? (прямые и кривые).

- Кто сможет показать, как я чертила кривые линии? Начертите рядом еще кривые линии. (Дети выходят и мелом чертят их).

- А как начертить прямые? (Дети пытаются начертить без линейки – не получается. Постепенно приходят к выводу – нужна линейка).

- Кто ответит - при помощи чего вычерчивают прямые и кривые линии? (прямые - при помощи линейки, а кривые – без нее как угодно).

- Итак, какие линии мы чертили? (прямые и кривые).

1. Учитель вызывает к доске двух учеников и дает им в руки – концы шнура (или ленты).

- Встаньте так, чтобы у вас получилась прямая линия. (Дети, держат шнур за концы и отходят друг от друга так, чтобы шнур был натянут).

- А теперь что нужно сделать, чтобы линия получилась кривая? (Нужно приблизиться, шагнуть друг к другу).

- Еще раз образуйте прямую линию. (Дети отходят так, чтобы шнур натянулся).

2. Учитель берет в руки ножницы, подходит к детям, которые держат шнур, отрезает его с двух сторон и к месту среза приставляет магнит красного цвета:

Двое детей, стоящие у доски, держат в руках отрезанный шнур и магнит.

- Что я сделала со шнуром? (Отрезали)

- Была прямая линия. Как ее теперь можно назвать. (Если дети сами не догадываются можно объяснить, что в математике эту фигуру называют отрезок).

3. На магнитной доске учитель крепит два магнита и через них перевешивает нитку.

- При помощи двух магнитов и шнура какую фигуру я смогу изобразить? (отрезок).

- Чтобы начертить на доске кривую – что нам потребуется в помощь? (мел).

- Что еще нужно, чтобы начертить прямую? (мел, линейка)

- А как мне начертить прямую? Это часть прямой или кривой линии? (часть прямой).

- Что еще мы делали с прямой линией, когда из нее образовывали отрезок? (мы ее отрезали и на место показывали магнитом).

- Как это сделать на доске? Что поставим вместо магнита? (Точки).

- Сколько точек нужно поставить, чтобы провести один отр<