Методы вычисления определителей n - го порядка: разложение определителя, метод понижении порядка

Свойства определителей.

Методы вычисления определителей n - го порядка: разложение определителя, метод понижении порядка

Любой определитель n-го порядка можно вычислить на основании следующей теоремы.

Теорема 1. Определитель n-го порядка равен сумме произведений элементов любой его строки (столбца)

на их алгебраические дополнения.

Замечание1: Вычисление определителя по данной теореме называют разложением определителя по

элементам строки или столбца (далее-ряда).

Метод понижения порядка определителя:

Этот метод также основан на элементарных преобразованиях определителя.

1. При помощи элементарного преобразования III типа нужно в одном столбце (или одной строке) сделать равными нулю все элементы, за исключением одного.

2. Разложить определитель по этому столбцу (строке) и получить определитель меньшего порядка, чем исходный. Если его порядок больше 1, то следует перейти к п. 1, иначе вычисления закончить.

Система n линейных уравнений с n неизвестными, ее решение методом Крамера.

Понятие матрицы. Виды матриц.Действия над матрицами и их свойства.

Матрицей размерности (m*n) называется совокупность чисел, расположенных в виде прямоугольной таблицы, содержащей m строк и n столбцов.

6. Обратная матрица, теорема о ее существовании. Алгоритм нахождения обратной матрицы.

Матричная форма записи систем n линейных уравнений с n неизвестными и ее решение с помощью обратной матрицы.

Модель равновесных цен.

Вектора и действия над ними.

Основные определения:

Определение 1.Величина, полностью характеризуемая своим числовым значением в выбранной системе единиц, называется скалярной или скаляром.

(Масса тела, объем, время и т.д.)

Определение 2. Величина, характеризуемая числовым значением и направлением, называется векторной или вектором.

(Перемещение, сила, скорость и т.д.)

Обозначения: 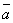, 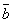или , .

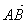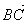Геометрический вектор – это направленный отрезок.

Для вектора 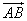– точка А – начало, точка В – конец вектора.

Определение 3. Модульвектора – это длина отрезка AB.

Определение 4.Вектор, модуль которого равен нулю, называется нулевым, обозначается .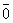

Определение 5.Векторы, расположенные на параллельных прямых или на одной прямой называются коллинеарными. Если два коллинеарных вектора имеют одинаковое направление, то они называются сонаправленными.

Определение 6.Два вектора считаются равными, если они сонаправлены и равны по модулю.

Действия над векторами:

Сложение векторов.

Опр. 6. Суммой двух векторов 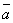и 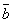является диагональ параллелограмма, построенного на этих векторах, исходящая из общей точки их приложения (правило параллелограмма).

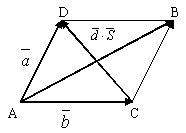
Рис.1.

Опр. 7.Суммойтрех векторов 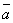, , 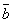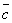называется диагональ параллелепипеда, построенного на этих векторах (правило параллелепипеда).

Опр. 8.Если А, В, С – произвольные точки, то 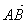+ 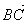= 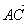(правило треугольника).

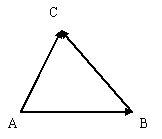
рис.2

Свойства сложения.

1^о. 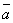+ 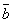= 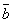+ 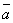(переместительный закон).

2^о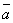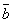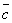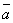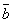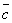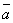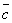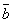. + ( + ) = ( + ) + = ( + ) + (сочетательный закон).

3^о. + (– ) + .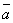

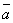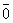Вычитание векторов.

Опр. 9.Подразностью векторов 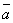и 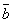понимают вектор 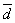= 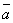– 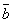такой, что + = .

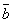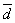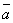В параллелограмме – это другая диагональ СД (см.рис.1).

Умножение вектора на число.

Опр. 10. Произведением вектора 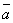на скаляр k называется вектор

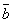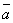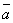= k = k,

имеющий длину ka, и направление, которого:

1. совпадает с направлением вектора 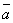, если k > 0;

2. противоположно направлению вектора 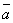, если k < 0;

3. произвольно, если k = 0.

Гипербола.

Г. наз-сягеометрическое множество точек, сумма расстояний от которых до 2х данных точек наз-ся фокусами есть величина постоянная равная 2а.

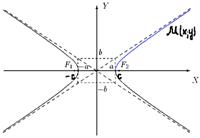а-точка пересечения по Ox. .

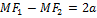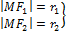– фокальные радиусы

Каноническое уравнение Г. имеет вид: 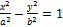, где .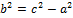

Свойства гиперболы:

1) Симметрична относит-но обеих осей координат.

2) Точка пересечение Г. с осью абсцисс наз-сядействительыми вершинами Г. Координаты имеют вид (a;0) (-a;0). Точки на оси ординат (0;b) (0;-b) – наз-ся мнимыми вершинами Г.

3) Ось абсцисс наз-ся действительной осью Г., а ось ординат-мнимой. a-действительная полуось, b-мнимая

4) Фокусы Г. – 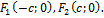Они всегда расположены на действительной оси, поэтому действит.ось иногда наз-ся фокальной. Расстояние между фокусами = 2с,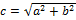

5) Отношение фокального расстояния 2с к длине действит.оси 2а наз-ся эксцентриситетом гиперболы, т.е.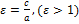

6) Если b=a, то Г.наз-ся равнобочной: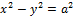

7) Асимптоты кривой y=f(x) наз-ся прямая y=kx+b, к которой неограничено приближаются ветви кривой при удалении ее точек в бесконечность. Прямые 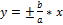явл-ся асимптотами Г.

8) Фокальные радиусы находятся как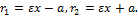

9) Если ур-ие Г. Задать в виде формулы 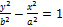, то мнимой осью будет ось абсцис, а действительной-ось ординат. Фокусы будут расположены на оси ординат и иметь координаты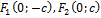

Парабола

П. наз-сягеометрич. место точек, равноудаленных от данной точки называемой фокусом, и от данной прямой, называемой директрисой. Расстояние от фокуса F до директрисы наз-ся параметром параболы, и обознач-ся через p. 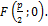А уравнение директрисы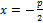

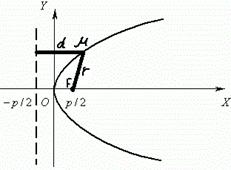
d-расстояние от точки М до директрисы. r-фокальный радиус

Уравнение параболы каноническое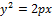

Свойства:

1) Обл.опред-ия[0;+∞)

2) Обл.значения (-∞;+∞)

3) Ветви направленны вправо

4) Вершина (0;0)

5) Парабола симетрична относит-но оси Ох

6) Эксцентриситетом П.наз-ся отношение фокального радиуса точки М к расстоянию d, от точки Ь до директрисы, т.е.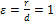

7) Фокальный радиус П.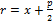

Общее ур-ие П: 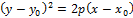– график1

Вершины параболы .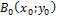

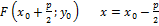
Если фокус лежит левее директрисы, то уравнение параболы 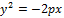– график2

Если фокус выше директрисы, то – график3 ( )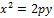

Если фокус ниже директрисы то – график4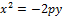

16.Прямая и плоскость в трехмерном пространстве и способы их задания. Взаимное расположение прямой и плоскости в пространстве.

Плоскость в трехмерном пространстве и способы ее задания:

Пусть дана плоскость в пространстве р. Любую плоскость в пространстве можно задать точкой 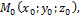лежащей на этой плоскости и ненулевым вектором 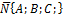( 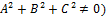, перпендикулярным этой плоскости.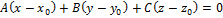

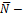нормальный вектор плоскости (нормаль)

Ax+By+Cz+D=0 – общее уравнение плоскости

Рассмотрим 2 плоскости 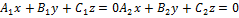. Нормаль у 1ой плоскости 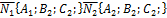. Угол между плоскостями равен углу, образованному между векторам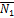и и .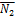

Cos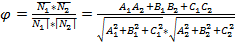

Две плоскости параллельны только тогда, когда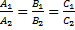

Две плоскости перпендикулярны, когда 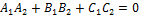(скалярное произведение 2х векторов).

Если выполняется условие 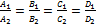, то плоскости сливаются

Плоскость р задается, если дана точка 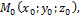лежащая на плоскост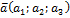и и 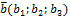, лежащие на плоскости и имеющие начало точку 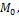векторы и не коллинеарны.

Уравнение плоскости: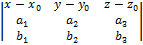

Прямая в трехмерном пространстве и способы ее задания:

Рассмотрим прямую в пространстве l. Она задается точкой 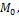которыя лежит на этой прямой и вектором 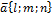-направляющий вектор. Тогда уравнение прямой

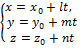
Параметрическое уравнение прямой t-некоторый параметр t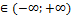

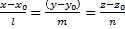– каноническое уравнение прямой

Пусть даны 2 точки 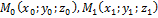тогда уравнение прямой имеет вид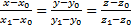

Прямую в пространстве можно задать как линию пересечения 2х плоскостей:

(1)

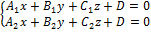
Для того, чтобы найти точку 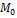, необходимо решить (1). Один из неизвестных можно задать произвольны значением. находится как векторное произведение нормальных векторов.

Пусть даны 2 прямые ,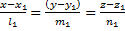

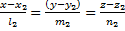
Углом 2х прямых наз-ся любой из 2х углов, образуемых 2мя прямыми соответственно параллельными данным прямым и проходящими через 1 точку

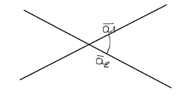
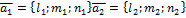
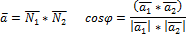
Две прямые перпендикулярны тогда и только тогда, когда выполняется следующее равенство

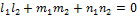
Две прямые параллельны тогда и только тогда, когда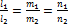

Взаимное расположение прямой и плоскости в пространстве:

Пусть дана плоскость Ax+By+Cz+D=0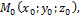

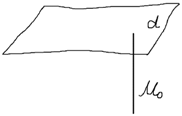
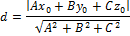
Пересекающиеся плоскости

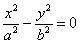
Мнимые пересекающиеся плоскости

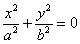
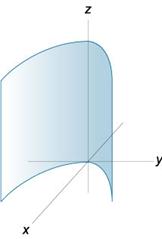
Параболический цилиндр

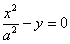
Параллельные плоскости

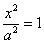
Мнимые параллельные плоскости

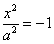
Совпадающие плоскости

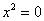
Уравнение сферы с центром в начале координат
Сфера является частным случаем эллипсоида, когда все его полуоси одинаковы (и равны радиусу сферы). Уравнение сферы с центром в начале координат и радиусом R выражается формулой
x² + y² + z² = R².

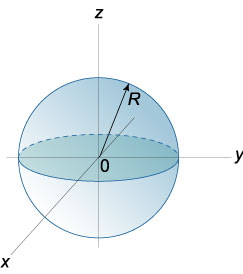
Общее уравнение сферы
Ax² + Ay² + Az² + Dx + Ey + Fz + M = 0, (A ≠ 0)
Центр сферы имеет координаты (a, b, c), где

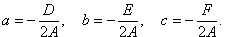
Радиус сферы равен

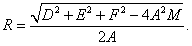
Замечания.

1. Совокупность всех собственных значений матрицы (с учетом их кратностей) называют ее спектром.

2. Спектр матрицы называется простым, если собственные значения матрицы попарно различные (все корни характеристического уравнения простые).

3. По основной теореме алгебры характеристическое уравнение имеетn в общем случае комплексных корней (с учетом их кратностей). Поэтому собственные значения и собственные векторы имеются у любой квадратной матрицы. Причем собственные значения матрицы определяются однозначно (с учетом их кратности), а собственные векторы — неоднозначно.

Понятие квадратичной формы.

Критерий Сильвестра.

Теорема. Для того чтобы квадратичная форма (19) была положительно (отрицательно) определённой, необходимо и достаточно чтобы все собственные значения 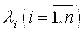её матрицы 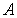были положительны (отрицательны).

Если квадратичная форма (19) произвольным образом приведена к каноническому виду (22), то она будет положительно (отрицательно) определённой, если 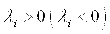для всех .

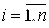Этот сложный путь определения характера знакоопределённости квадратичной формы можно обойти, исследуя главные миноры матрицы .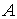

Такой способ установления характера знакоопределённости квадратичной формы называется Критерием Сильвестра и состоит в следующем:

1) для того чтобы квадратичная форма (19) была положительно определённой необходимо и достаточно, чтобы все главные диагональные миноры матрицы 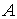этой квадратичной формы были положительны:

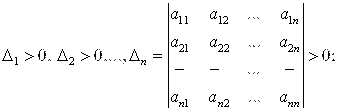
2) для того чтобы квадратичная форма (19) была отрицательно определённой, необходимо и достаточно, чтобы знаки главных диагональных миноров матрицы 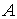этой квадратичной формы чередовались, начиная со знака «–» для , т. е.

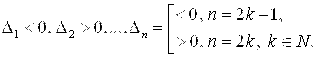
Общая задача оптимизации.

Свойства определителей.

Методы вычисления определителей n - го порядка: разложение определителя, метод понижении порядка

Любой определитель n-го порядка можно вычислить на основании следующей теоремы.

Теорема 1. Определитель n-го порядка равен сумме произведений элементов любой его строки (столбца)

на их алгебраические дополнения.

Замечание1: Вычисление определителя по данной теореме называют разложением определителя по

элементам строки или столбца (далее-ряда).

Метод понижения порядка определителя:

Этот метод также основан на элементарных преобразованиях определителя.

1. При помощи элементарного преобразования III типа нужно в одном столбце (или одной строке) сделать равными нулю все элементы, за исключением одного.

2. Разложить определитель по этому столбцу (строке) и получить определитель меньшего порядка, чем исходный. Если его порядок больше 1, то следует перейти к п. 1, иначе вычисления закончить.