Определяем адекватность уравнения регрессии.

5.. Из таблицы лабораторной работы № 2 выбираем столбец теоретических значений 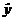. Переносим его в нашу таблицу.

Номер опыта	Экспериментальные значения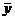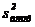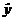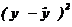
y1	y2
					69.79981191
					68.02438266
					80.84481097
					60.06938173
		70,5	70.25	0.125	70.36169304
			67.5	0.5	66.5862638
					83.4066921
					78.63126286
					77.19986079
		67,5	67.25	0.125	67.75271426
					69.1957804
			79.5	0.5	77.75545426
		66,5	66.25	0.125	66.40320533
					72.55339091
					71.41725078
Сумма столбца	-	-	-	3,375	-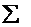

6. Для определения остаточной дисперсии заполняем последний столбец таблицы – находим квадратичную разность 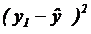в каждой строке.

Номер опыта	Экспериментальные значения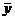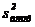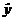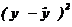
y1	y2
					69.79981191	0.040075273
					68.02438266	0.951829185
					80.84481097	0.713705577
					60.06938173	0.004813824
		70,5	70.25	0.125	70.36169304	0.130821854
			67.5	0.5	66.5862638	0.171177646
					83.4066921	1.978782671
					78.63126286	0.398492799
					77.19986079	3.240501167
		67,5	67.25	0.125	67.75271426	0.566578762
					69.1957804	1.429890763
			79.5	0.5	77.75545426	5.037985569
		66,5	66.25	0.125	66.40320533	0.162574539
					72.55339091	2.092677869
					71.41725078	2.008599766
Сумма столбцов	-	-	-	3,375	-	18.92850727

Теперь по формуле считаем остаточную дисперсию :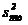

.

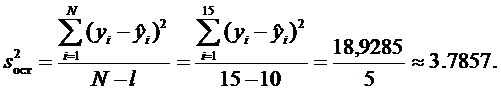По критерию Фишера:

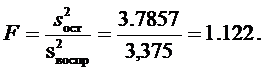
Определим табличное значение критерия Фишера:

Уровень значимости p=0.05;

число степени свободы f₁:

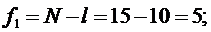
число степени свободы f₂:

.

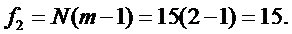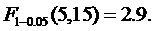
Получаем

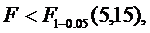
значит уравнение адекватно эксперименту.

Лабораторной работы № 4

ОПТИМИЗАЦИЯ МЕТОДОМ КРУТОГО ВОСХОЖДЕНИЯ

БОКСА-УИЛСОНА

Цель работы. Задача оптимизации ставится таким образом: необходимо определить экспериментально координаты экстремальной точки для заданной функции.

Основные положения.

Оптимизация процесса – поиск наилучших условий его проведения. Задачи оптимизации приходится решать при разработке новых технологий и реконструкции действующих производств [3].

Суть всех градиентных методов заключается в использовании вектора градиента 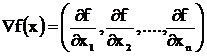для определения направления движения к оптимуму. Вектор градиента обладает свойствами, которые и обуславливают его эффективное применение при поиске экстремальных значений функции многих переменных. Вектор градиента всегда направлен в сторону наиболее быстрого возрастания функции в данной точке. Поэтому очевидно, что при поиске минимальных значений функции необходимо двигаться в противоположную сторону. Такое направление движения называют антиградиентом или отрицательным градиентом и оно охарактеризует направление наиболее быстрого убывания функции.

Метод крутого восхождения Бокса-Уилсона представляет собой пошаговую процедуру движения по поверхности отклика, в которой для оценки составляющих градиента 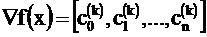используется линейное уравнение регрессии 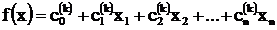, полученное в результате планирования эксперимента в окрестности точки .

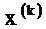Затем совершается движение по поверхности отклика в направлении градиента с величиной шага, пропорциональной произведению коэффициента 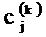на шаг варьирования 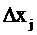. Движение по поверхности осуществляется до тех пор, пока параметр оптимизации не начнет увеличиваться (в случае поиска минимума). В полученной точке вновь производится планирование эксперимента и оценка нового направления движении. Процедура поиска продолжается до тех пор, пока величина вектора градиента не станет меньше заданной точности [2].

Для выполнения лабораторной работы № 4 будет необходимо использовать данные, полученные в лабораторной работе № 2.

Двухфакторный эксперимент.

1. Выписываем посчитанные при выполнении лабораторной работы № 2 значения шагов варьирования переменных h_1, h_2, и значения основных уровней 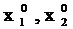соответственно варианту.

2. В уравнении регрессии, найденном также в лабораторной работе № 2 переходим от кодированных координат к натуральным. Переход осуществляется по формуле:

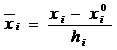
где – значение переменной в кодированных координатах, - значение переменной в натуральных координатах.

Подставим данной выражение в уравнение регрессии.

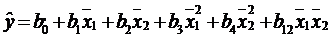
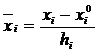
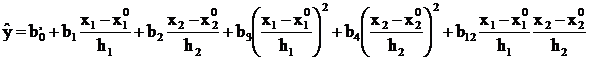
Выполним преобразования и получим уравнение регрессии в натуральном масштабе:

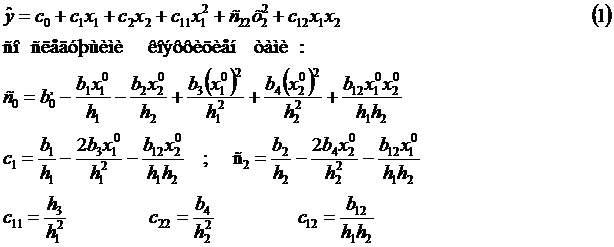
При проведении расчетов заполняем таблицу:

Номер опыты		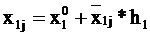	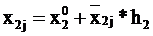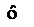(считается по формуле (1))

3. Вычислим величину шага для имеющихся переменных (факторов) - :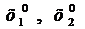

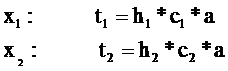
где а – коэффициент пропорциональности, который может принимать любые значения (обычно берут равным 0,1)

4. Начинаем движение по поверхности отклика из начальной точки 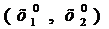. Движение по поверхности осуществляется в сторону противоположную градиенту функции до тех пор, пока значение функции не начнет увеличиваться, в случае поиска минимума. В случае поиска максимума движение происходит в сторону градиента функции до того момента, пока значения функции не начнут уменьшаться.

Наша задача – пройти поверхность отклика в обе стороны с целью определения экстремума функции.