Методы обработки результатов измерений
ОСНОВЫ НАУЧНЫХ ИССЛЕДОВАНИЙ
Волгоград
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ВОЛЖСКИЙ ПОЛИТЕХНИЧЕСКИЙ ИНСТИТУТ (филиал)
ВОЛГОГРАДСКОГО ГОСУДАРСТВЕННОГО ТЕХНИЧЕСКОГО УНИВЕРСИТЕТА
С.В. Лапшина
ОСНОВЫ НАУЧНЫХ ИССЛЕДОВАНИЙ
Лабораторный практикум
Учебное пособие
РИК «Политехник»
Волгоград
УДК
Рецензенты:
Профессор Волгоградского государственного университета, доктор физико-математических наук Горяйнов И.Ю.
Доцент Волгоградского государственного университета, кандидат физико-математических наук Лосева Н.В.
Лапшина С.В.
Основы научных исследований: Учеб. пособие / С.В. Лапшина. ВПИ (филиал) ВолгГТУ. - Волгоград, 2012. – с.
ISBN 978-5-9948-0054-6
В учебном пособии рассматриваются лабораторные работы по курсу «Основы научных исследований».
Учебное пособие предназначено для студентов, обучающихся по специальности 240801.65”Машины и аппараты химических производств”, а также для студентов обучающихся по направлению по направлению 241000.62 «Энерго- и ресурсосберегающие процессы в химической технологии, нефтехимии и биотехнологии».
Ил. 11 . Табл. 30 . Библиогр. : назв.
Печатается по решению редакционно-издательского совета
Волгоградского государственного технического университета
ISBN 978-5-9948-0054-6
Ó Волгоградский государственный технический университет, 2012
Введение
При подготовки дипломированного специалиста по специальности 240801.65 «Машины и аппараты химических производств» и бакалавра по направлению 241000.62 «Энерго- и ресурсосберегающие процессы в химической промышленности, нефтехимии и биотехнологии» изучается дисциплина «Основы научных исследований». Для полного освоения дисциплины и приобретения навыков практических расчетов и выполнения анализа полученных данных курс «Основы научных исследований» включает в себя выполнения лабораторных работ.
Учебное пособие разработано для студентов очной, очно-заочной и заочной формы обучения. Учебное пособие предназначено для выполнения и подготовки к отчету по лабораторным работам.
ЛАБОРАТОРНАЯ РАБОТА №1
АНАЛИЗ СЛУЧАЙНЫХ ВЕЛИЧИН
Цель работы. Найти наивероятнейшее значение измеряемой величины (среднее арифметическое 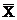 ), точности полученных результатов, среднюю квадратическую и наибольшую ошибки среднего арифметического.
), точности полученных результатов, среднюю квадратическую и наибольшую ошибки среднего арифметического.
Основные положения.
Одним из важнейших основных понятий теории вероятностей является понятие о случайной величине.
Случайной величиной называется величина, которая в результате опыта может принять то ли иное значение, причём неизвестно заранее, какое именно. Говоря о значениях случайной величины, мы подчеркиваем тем самым, что они (значения) могут быть получены путём тех или иных измерений. Если ожидаемые результаты измерений можно заранее отделить друг от друга, то соответствующие им случайные величины называются дискретными (число попаданий при пяти выстрелах, количество годных деталей в партии из заранее оговоренного их числа и т.п.). В то же время существуют случайные непрерывные величины, когда возможные их значения не могут быть перечислены, не отделены друг от друга, заполняют непрерывно некоторый промежуток (дальность полёта снаряда, ошибка взвешивания тела на весах и т.п.).
При рассмотрении любой дискретной случайной величины можно установить связь межу конкретным её значением и частотой появления этого значения (в пределе частота событий будет равна вероятности событий). Всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями называются законом распределения этой величины.
Простейшей формой задания закона распределения является таблица с приведёнными в ней возможными значениями случайной величины хi соответствующими им вероятностями (ряд распределения). Пример такого ряда распределения приведён в табл. 1.
Таблица 1
Табличные распределения
| хi | |||||
| pi | 0,1 | 0,2 | 0,4 | 0,2 |
Поскольку дискретные величины являются несовместными, то полная сумма их вероятностей 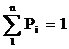 Для придания ряду распределения наглядного вида часто изображают его графически, получая многоугольник распределения.
Для придания ряду распределения наглядного вида часто изображают его графически, получая многоугольник распределения.
Пример, соответствующий данным, приведенным в табл. 1, показан на рис. 1.
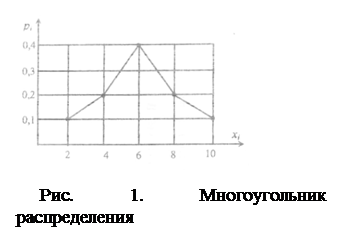
Ряд распределения дает исчерпывающую характеристику случайной величины, но построить его для непрерывной случайной величины нельзя, так как невозможно перечислить все ее возможные значения. Для количественной характеристики такого распределения удобно воспользоваться не вероятностью события Х=хi а вероятностью события Х<хi, и ввести понятие функции распределения, называемой иногда интегральной функцией распределения:
F(xi) = p(X<xi). (1)
Она имеет следующие общие свойства:
1) функция распределения F(хi) есть неубывающая функция своего аргумента;
2) на минус бесконечности функция распределения равна нулю, то есть F(-∞) = 0;
3) на плюс бесконечности функция распределения равна единице, то есть F(+∞) = 1.
Функция распределения - универсальная характеристика случайной величины. Она существует и для непрерывных, и для дискретных случайных величин. Так, для примера, приведенного в табл 1, график функции распределения показан на рис. 2.
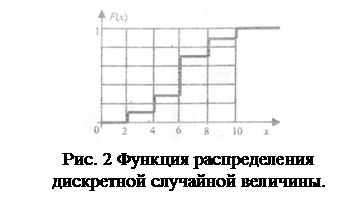
Если на некоторых участках случайная величина будет изменяться непрерывно, то на данных участках F(xi) будет плавно возрастать. Если же случайная величина непрерывна на всех участках, го она примет вид кривой, приведенной на рис. 3.
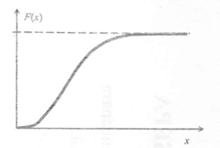 |
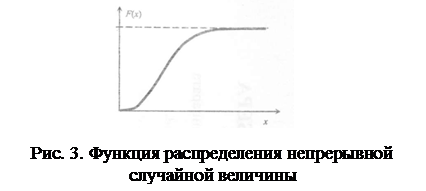
 |
Как следует из определения функции F(x), что и отражено на рис 2 и 3, функция распределения дискретной величины изображается ступенчатой линией, а функция распределения непрерывной случайной величины в виде плавной возрастающей линии
Важной характеристикой случайной величины является ее плотность вероятности, или плотность распределения. Так называют предел отношения вероятности попадания значения случайной величины в бесконечно малый интервал (х, х + Δх) к длине этого интервала
Δх: 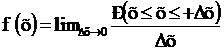 (2)
(2)
что, собственно, является производной функции распределения.
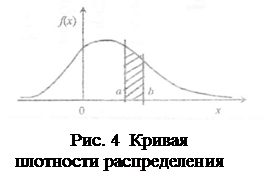 Вид кривой плотности распределения для общего случая показан на рис. 4.
Вид кривой плотности распределения для общего случая показан на рис. 4.
Следует отметить, что плотность распределения существует только для непрерывных случайных величин. Ее основные свойства:
1. Плотность распределения не является отрицательной величиной: f(х) ≥ 0.
2. Интеграл в бесконечных пределах от плотности распределения равен единице:
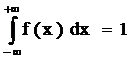 (3)
(3)
3. Вероятность попадания случайной величины х в интервал а, b (см. рис. 3.6) определяется равенством:
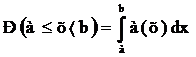 (4)
(4)
4. Функция распределения F(x) может быть выражена через плотность распределения:
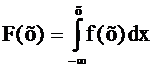 (5)
(5)
Плотность распределения являстся одной из форм закона распределения. Среди законов распределения большое значение имеют биномиальное распределение, распределение Пуассона.
Биномиальное распределение. Как отмечалось выше, каждый член разложения численно равен вероятности некоторого события А, характерного тем, что при известной вероятности Р его появления в каждом единичном опыте оно появится т раз из возможного числа N всех испытаний. Общий член разложения удобнее представить в виде:
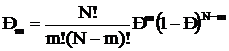 (6)
(6)
Эта формула и представляет собой закон биномиального распределения. Поскольку величины m могут принимать только вполне определенные целые значения, то данное распределение относится только к дискретным случайным величинами. График биномиального распределения представляет собой ломаную линию, форма которой зависит от значений Р, т и N. На рис. 5
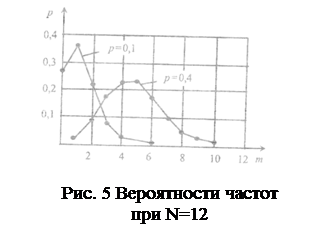
Распределение Пуассона. Рассматривая закон биномиального распределения (6), можно задать следующие условия: число опытов N стремится к бесконечности, а вероятность Р стремится к нулю, при этом их произведение a = N*Р сохраняет постоянное значение. Такое предельное представление биномиального распределения называется распределением Пуассона и может быть выражено, как показывает Е. С. Вентцель [1], формулой
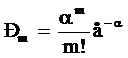 (7)
(7)
позволяющей найти для записанных выше условий вероятность появления некоторого события А при большом числе N независимых опытов, в каждом из которых событие А имеет очень малую вероятность Р.
Иногда распределение Пуассона называют законом редких явлений. Покажем его применение на примере. Пусть известно, что на ткацком станке нить обрывается в среднем 0,25 раза за один час работы станка (Р=0,25). Определить вероятность того, что за восемь часов работы произойдет три обрыва нити (т=3).
Для решения определим 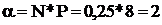 и по формуле (7) получаем искомый результат:
и по формуле (7) получаем искомый результат: 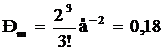
Из формулы (6) можно получить вероятность появления события хотя бы один раз в некоторой группе N:
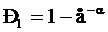 (8)
(8)
Зависимость (8) используют для решения, например, таких задач: определить вероятность поражения малоразмерной цели при стрельбе по площади.
Пусть известно, что цель площадью S=0,6 м2 находится в некотором осколочном поле, характеризующимся двумя попаданиями на один квадратный метр. Если для поражения цели достаточно попадания в нее хотя бы одного осколка, то вероятность такого события при 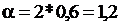 будет равна:
будет равна:
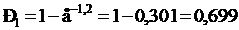
Нормальное распределение. Расчет вероятностей по формуле (6) при больших N весьма громоздок; с учетом прерывности величины m аналитическое отыскание суммы вероятностей для областей с некоторыми границами затруднителен. Как показано в [3], в предельном случае (N→∞, m – любое число, в том числе и не целое, P=0,5) закон биномиального распределения можно выразить иначе. Новое его выражение называется законом нормального распределения (законом Гаусса), а плотность вероятности в этом случае будет:
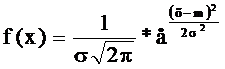 (9)
(9)
где т - математическое ожидание величины х; σ - среднее квадра- тическое отклонение величины х (определение величин m и σ будет дано ниже).
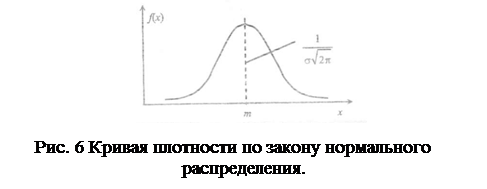
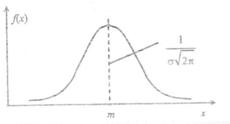
Кривая по закону нормального распределения имеет симметричный вид, при этом максимальная ордината кривой равна 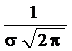 в точке х=т; по мере удаления от точки m плотность распределения уменьшается, а при х → ± ∞ кривая асимптотически приближается к оси абсцисс. Поскольку площадь под кривой плотности в любом случае равна единице, то параметр σ влияет на форму кривой, вытягивая ее вверх при уменьшении значения σ.
в точке х=т; по мере удаления от точки m плотность распределения уменьшается, а при х → ± ∞ кривая асимптотически приближается к оси абсцисс. Поскольку площадь под кривой плотности в любом случае равна единице, то параметр σ влияет на форму кривой, вытягивая ее вверх при уменьшении значения σ.
 |
 |
Большинство встречающихся на практике случайных величин могут быть представлены как суммы весьма большого числа отдельных слагаемых, практически не зависящих друг от друга. Например, отклонения в попаданиях снарядов от средней точки прицеливания зависят от метеоусловий, отклонений в массе снаряда и т. д. Показано [2], что такая сумма приближенно подчиняется закону нормального распределения, при этом чем большее число факторов будет влиять на рассматриваемую случайную величину, тем ближе будет это распределение к теоретическому нормальному закону распределения.
Закон нормального распределения, имеющий глубокое теоретическое обоснование его свойств, используется в качестве основного во многих практических исследованиях, результаты опытов сравниваются именно с ним.
Порядок выполнения работы.
1. Выберите вариант задания из таблице случайных чисел.
2.Определите среднее арифметическое;
3. Найдите среднюю квадратическую ошибку отдельного измерения;
4. Определите наибольшую возможную ошибку 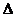 отдельного измерения и убедиться, что среди результатов измерений нет такий, которые отличались бы от среднего арифметического более чем на
отдельного измерения и убедиться, что среди результатов измерений нет такий, которые отличались бы от среднего арифметического более чем на 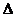 . Если бы таковые оказались, их следует отбросить и начать обработку сначала. Данные сведите в таблицу;
. Если бы таковые оказались, их следует отбросить и начать обработку сначала. Данные сведите в таблицу;
5. Определите среднюю квадратическую ошибку 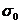 среднего арифметического.
среднего арифметического.
6. Определите характеристики 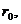
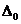 , h и H.
, h и H.
Таблица 2
| Исходные данные | Первая обработка | Вторая обработка | ||||
| № по пор. | 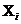 | 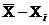 | ( 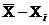 )2 )2 | 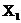 | 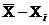 | ( 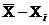 )2 )2 |
| i |
ЛАБОРАТОРНАЯ РАБОТА №2
ПЛАНИРОВАНИЕ МНОГОФАКТОРНОГО ЭКСПЕРИМЕНТА
Цель работы.
Построение математической модели изучаемого объекта с использованием планирования эксперимента.
Основные положения.
Большое количество экспериментальных задач в химии и химической технологии формулируется как задачи экстремальные: определение оптимальных условий процесса, оптимального состава композиции и т.д. Планирование эксперимента резко повышает точность и уменьшает объем экспериментальных исследований. Поэтому использование метода планирования эксперимента является наиболее эффективным методом получения математических моделей многофакторного процесса. При его реализации можно оценить роль факторов. на которые можно воздействовать (температура, концентрации, давления и др. ) при исследовании и оптимизации изучаемого объекта или технологического процесса, получить количественные основных эффектов взаимодействия. Выбор плана определяется постановкой задачи исследования и особенностями объекта. Процесс исследования обычно разбивается на отдельные этапы. Информация, полученная после каждого этапа, определяет дальнейшую стратегию эксперимента. Таким образом возникает возможность оптимального управления экспериментом. Применение методов планирования значительно повышает эффективность эксперимента [3].
Рассмотрим основные определения, сущность и задачи планирования эксперимента; порядок построения модели исследуемого процесса при помощи полного факторного эксперимента, особенности построения моделей с учетом нелинейностей типа квадрата факторов, а также расчетные формулы для обработки и оценки экспериментальных данных.
Переменные x1, x2, …, xk принято называть факторами. Факторами могут быть какие-либо внешние для объекта исследования воздействия (влажность, температура окружающей среды), или же параметры самого объекта (концентрация, температура, давление, удельная теплоемкость рабочей смеси). Выходные параметры также могут быть разнородными. В зависимости от решаемой задачи выходная величина называется откликом, функцией цели, функцией отклика, параметром оптимизации. Обычно аналитическая связь между входом и выходом (модель объекта) неизвестна, а известны факторы xi и подлежащие исследованию выходные величины yi.
Область определения двух факторов x1, x2 называется двухфакторным пространством, а эксперимент – двухфакторным экспериментом.
Каждый фактор может принимать определенное количество значений. Эти значения называются уровнями факторов. Например, если факторы могут принимать два значения -1, +1, то число уровней равно 2.
Число опытов в одном эксперименте равно числу различных наборов факторов. Для полного факторного эксперимента необходимое количество опытов N определяется по формуле:
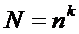 ,
,
где n – количество уровней; k – число факторов.
При проведении двухфакторного эксперимента на двух уровнях результат эксперимента представляет собой квадрат и число опытов равно:
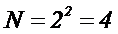 .
.
При проведении трехфакторного эксперимента на двух уровнях результат эксперимента представляет собой куб или параллелепипед, число вершин которого равно числу опытов:
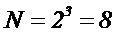 .
.
Выбор факторов.Приступая к планированию эксперимента, необходимо выбрать факторы и определить: влияние их на выходную величину y, какие из них могут задаваться по желанию экспериментатора, какие неуправляемы или случайны, являются ли факторы зависимыми или независимыми величинами.
Для каждого эксперимента необходимо выбрать интервал варьирования факторов h, которым называется половина разности между верхним и нижним значениями фактора:
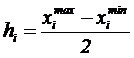
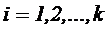 .
.
Интервал варьирования физического фактора должен быть таким, чтобы его величина примерно на порядок превосходила погрешность установки и измерения величины xi; аппроксимирующая функция незначительно отличалась от искомой зависимости – требование адекватности модели; при переходе от одного опыта к другому изменение отклика было достаточно ощутимым, т.е. в несколько раз превосходило погрешность отклика.
Значение фактора в центре области эксперимента называется его основным уровнем или центром плана, обозначается 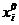 и может быть найдено следующим образом:
и может быть найдено следующим образом:

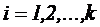 .
.
Для удобства записи плана эксперимента и обработки экспериментальных данных обычно пользуются условными значениями факторов, которые обозначаются 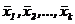 и вычисляются по формуле:
и вычисляются по формуле:
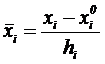
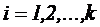 .
.
Данная процедура равносильна переносу начала координат в точку основного уровня факторов и изменению масштаба. Все условные факторы – безразмерные и нормированные величины.
Модель процесса. Выбор модели (уравнения модели) в методе планирования эксперимента – неформализованный этап, который основывается обычно на интуитивных соображениях с учетом предыдущего опыта экспериментатора, а количественное определение коэффициентов выбранных уравнений модели – на результатах эксперимента. Поэтому правильный выбор модели должен подтверждаться экспериментально.
Модель определяется переменными xi и постоянными параметрами βi и в общем случае имеет вид:
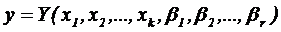 .
.
Модели могут быть линейные относительно xi:
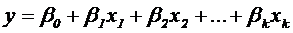 ,
,
Также они могут быть нелинейного вида:
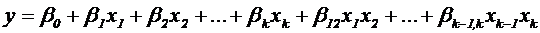
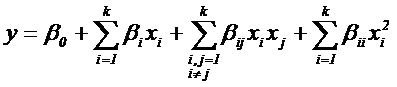
Построение планов полного факторного эксперимента. Полным факторным называется такой эксперимент, в котором реализуются все возможные комбинации (наборы) уровней факторов. Если k факторов варьируются на двух уровнях, то число всех возможных наборов – N=2k. Если k факторов варьируются на трех уровнях, то N=3k. С увеличением числа факторов k, быстро растет число опытов.
Используя полученные данные можно представить план эксперимента в виде таблицы матрицы. Для двухфакторного эксперимента:
| Номер опыта | Уровни переменных | Отклики | |||
| x1 | x2 | yu1 | yu2 | yuj | |
| -1 | -1 | y11 | y12 | y1j | |
| +1 | -1 | y21 | y22 | y2j | |
| -1 | +1 | y31 | y32 | y3j | |
| +1 | +1 | y41 | y42 | y4j |
Для трехфакторного эксперимента:
| Номер опыта | Уровни переменных | Отклики | ||||
| x1 | x2 | x3 | yu1 | yu2 | yuj | |
| -1 | -1 | -1 | y11 | y12 | y1j | |
| +1 | -1 | -1 | y21 | y22 | y2j | |
| -1 | +1 | -1 | y31 | y32 | y3j | |
| +1 | +1 | -1 | y41 | y42 | y4j | |
| -1 | -1 | +1 | y51 | y52 | y5j | |
| +1 | -1 | +1 | y61 | y62 | y6j | |
| -1 | +1 | +1 | y71 | y72 | y7j | |
| +1 | +1 | +1 | y81 | y82 | y8j |
В каждой точке может проводиться несколько опытов nu, которые называются параллельными. Для проведения эксперимента значения факторов разделяются на уровни, задаваемые соответствующими строками.
Основные достоинства планов ПФЭ – простота определения коэффициентов уравнения регрессии, возможность учета произведений взаимодействия факторов без изменения плана основного эксперимента. Преимущества любой матрицы ПФЭ достигаются за счет особого построения плана эксперимента, при котором матрица обладает свойствами ортогональности, нормировки, симметрии и ротатабельности.
Свойство ортогональности: сумма построчных произведений элементов любых двух граф равно нулю.
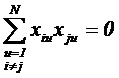
где i, j – номер столбца или номер фактора; i=1,2,…, k (k – общее количество факторов); u – номер набора факторов или номер строки; N – общее число различных наборов или число строк матрицы ПФЭ.
Свойство нормировки: сумма квадратов элементов любой графы равна числу различных опытов – строк N.
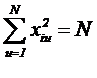
Свойство симметрии: алгебраическая сумма элементов любого реального фактора равна нулю (условие баланса положительных и отрицательных значений каждой переменной).
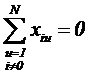
Свойство ротатабельности: дисперсии предсказанных значений отклика на равных расстояниях от центра плана постоянны и минимальны.
В полном факторном эксперименте возможен учет нелинейностей типа произведения факторов (уравнение регрессии отличается от линейного наличием слагаемого xixj) и учет нелинейностей типа квадратов факторов.
План, учитывающий нелинейности типа квадратов факторов, называется ортогональным центрально-композиционным планом (ОЦКП) второго порядка. Они позволяют сформировать функцию отклика в виде полного квадратичного полинома, который содержит большее число членов, чем неполный квадратичный полином, сформированный по планам первого порядка, и поэтому требуют большего числа выполняемых опытов.
В общем случае для k факторов полином второй степени имеет вид:
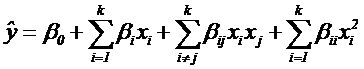
Полный квадратичный полином при k=2 содержит 6 членов и имеет вид:
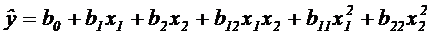
при k=3 – 11 членов:
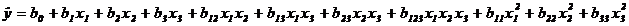
Для получения квадратичной зависимости каждый фактор должен фиксироваться как минимум на трех уровнях.
Планы ПФЭ не позволяют найти коэффициенты βii при квадратах факторов, так как все графы 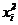 тождественны графе x0 (xi=±1,
тождественны графе x0 (xi=±1, 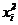 =1). Кроме того, для этих граф нарушаются условия ортогональности и симметричности. В основе построения планов второго порядка, как и планов первого порядка, лежат принципы ортогональности граф и их симметрия. Условие нормировки может не выполняться.
=1). Кроме того, для этих граф нарушаются условия ортогональности и симметричности. В основе построения планов второго порядка, как и планов первого порядка, лежат принципы ортогональности граф и их симметрия. Условие нормировки может не выполняться.
Для выполнения этих принципов к центру плана второго порядка, ядру – 2k добавляются дополнительные точки факторного пространства. Точки называются звездными. Положение звездных точек определяется из условия ортогональности всех граф матрицы планирования второго порядка. Кроме значений факторов на уровнях ±1, в плане добавляется точка начала координат xi=0 (i=1, 2,…,k) и на каждой координате выбираются две звездные точки xi=α.
Общее число опытов определяется соотношением:
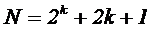
k – количество факторов.
На рисунке 1 показано проведение опыта в двухфакторном пространстве для плана ОЦКП. Звездные точки отмечены кружками. Величина α называется плечом звездных точекили звездным плечом. Положение звездных точек зависит от числа варьируемых факторов [3].
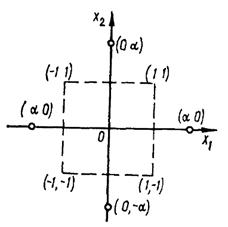
Рисунок 1 – расположение звездных точек.
Наличие звездных точек обеспечивает ортогональность граф первых степеней факторов. В ОЦКП каждый фактор фиксируется, в общем случае на пяти уровнях – -α, -1, 0, 1, α.
Для обеспечения ортогональности всех граф матрицы ОЦКП необходимо преобразовать квадраты факторов по формуле:
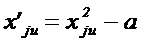
Значение поправки a определяется следующим образом.
Сумма элементов столбца, соответствующего квадратам факторов должна быть равна нулю:
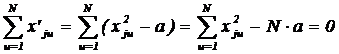
Откуда
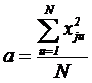 (1)
(1)
В общем случае ортогональный центрально-композиционный план при трех факторах имеет вид:
Таблица 1
| Номер опыта | x0 | x1 | x2 | x3 | x1∙x2 | x1∙x3 | x2∙x3 | x1∙x2∙x3 | 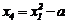 | 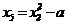 | 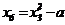 | y | |
| Точки плана ПФЭ 23 (N0=2k точек) | +1 | -1 | -1 | -1 | +1 | +1 | +1 | -1 | 1-a | 1-a | 1-a | y1 | |
| +1 | +1 | -1 | -1 | -1 | -1 | +1 | +1 | 1-a | 1-a | 1-a | y2 | ||
| +1 | -1 | +1 | -1 | -1 | +1 | -1 | +1 | 1-a | 1-a | 1-a | y3 | ||
| +1 | +1 | +1 | -1 | +1 | -1 | -1 | -1 | 1-a | 1-a | 1-a | y4 | ||
| +1 | -1 | -1 | +1 | +1 | -1 | -1 | +1 | 1-a | 1-a | 1-a | y5 | ||
| +1 | +1 | -1 | +1 | -1 | +1 | -1 | -1 | 1-a | 1-a | 1-a | y6 | ||
| +1 | -1 | +1 | +1 | -1 | -1 | +1 | -1 | 1-a | 1-a | 1-a | y7 | ||
| +1 | +1 | +1 | +1 | +1 | +1 | +1 | +1 | 1-a | 1-a | 1-a | y8 | ||
| Звездные точки (2k точек) | +1 | -α | α2-a | -a | -a | y9 | |||||||
| +1 | + α | α2-a | -a | -a | y10 | ||||||||
| +1 | - α | -a | α2-a | -a | y11 | ||||||||
| +1 | + α | -a | α2-a | -a | y12 | ||||||||
| +1 | - α | -a | -a | α2-a | y13 | ||||||||
| +1 | + α | -a | -a | α2-a | y14 | ||||||||
| Нулевая точка | +1 | -a | -a | -a | y15 | ||||||||
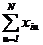 | - | N | - | ||||||||||
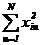 | - | N | 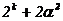 | 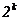 | 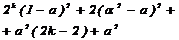 |
Для определения неизвестных a и α нужно сформировать и решить систему из двух уравнений. Одно из них для a было записано раннее – это уравнение (1). Другое уравнение получим из условия ортогональности для столбцов x4 и x5:
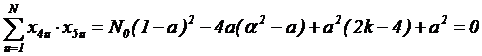 .
.
После простейших преобразований с учетом того, что 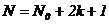 - общее число опытов в плане, получаем
- общее число опытов в плане, получаем
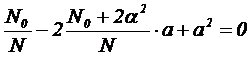 .
.
Соотношение для a при j=1, 2 или 3 может быть записано как (см. план):
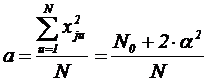 .
.
Подставив его в предыдущее уравнение получаем:
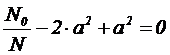
Откуда
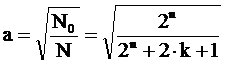 .
.
Тогда
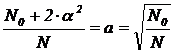 .
.
И плечо звездных точек
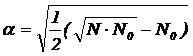
Например, для ОЦКП при числе факторов k=3 параметры плана следующие:
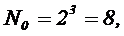
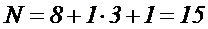
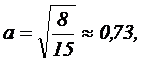
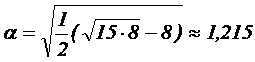
Обобщим результаты в таблицу 2.
Таблица 2
| Число факторов k | Ядро (центр) плана | Общее число опытов N | Звездное плечо α | Значение поправки a |
| 22 | 1.0000 | 2/3=0.6667 | ||
| 23 | 1.2154 | 8/15=0.7303 | ||
| 24 | 1.4142 | 4/5=0.80 | ||
| 25-1 | 1.5467 | 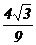 =0.7698 =0.7698 | ||
| 25 | 1.5960 | 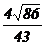 =0.8627 =0.8627 |
Располагая данными таблицы 3, можно построить ортогональные центрально-композиционные планы второго порядка.
По результатам опытов формируется полином.
при k=2:
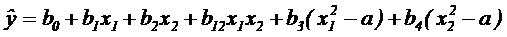
при k=3:
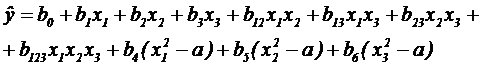
Коэффициенты полинома определяются по формуле:
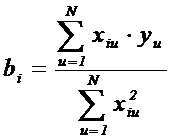
Полиномы можно представить в виде:
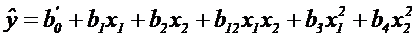 - при k=2;
- при k=2;
и при k=3:
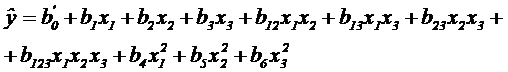
Где коэффициент 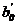 определяется следующим образом при k=2:
определяется следующим образом при k=2:
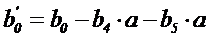
при k=3:
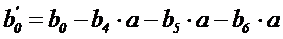
Ортогональные центрально композиционные планы при 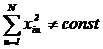 не обеспечивают постоянства дисперсии отклика в различных точках факторного пространства.
не обеспечивают постоянства дисперсии отклика в различных точках факторного пространства.
Порядок выполнения работы.
1. Выберете вариант задания из приложения 3. В соответствии с заданием выполните следующие пункты.
2. Оцениваем граничные значения факторов, центр плана, шаг варьирования.
Шаг варьирования:
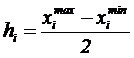
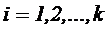
где 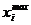 - верхнее граничное значение фактора;
- верхнее граничное значение фактора; 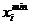 - нижнее граничное значение фактора.
- нижнее граничное значение фактора.
Значение фактора в центре области эксперимента называется его основным уровнем или центром плана, обозначается 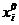 и может быть найдено следующим образом:
и может быть найдено следующим образом:

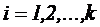
Граничные значения:
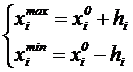
3. Переводим все значения факторов в условные единицы по формуле:
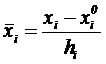
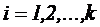
где 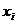 - значения фактора в натуральном масштабе,
- значения фактора в натуральном масштабе, 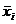 - значение фактора в условном масштабе.
- значение фактора в условном масштабе.
Для граничных условий и центра плана:

Результаты пересчета значений факторов из натуральных величин в условные сведем в таблицу:
Таблица 1
| № | Фактор | Основной уровень (в натуральных единицах) | Шаг варьирования (в натуральных единицах) | Значения уровней переменных соответствующие условным единицам | ||
| -1 | +1 | |||||
| 1. | ||||||
| 2. | ||||||
| 3. |
Построим ортогональный центрально-композиционный план (ОЦКП) второго порядка, который учитывает нелинейности типа квадрата факторов.
Схема планирования 2-факторного эксперимента
Полный квадратичный полином при k=2 содержит 6 членов и имеет вид:
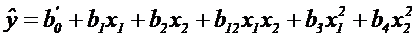
Общее число опытов вычисляется по формуле:
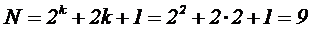
Звездное плечо:
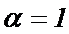
Значение поправки a:
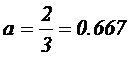
Все данные берем из таблицы, расположенной в пункте «Основные положения» в соответствии со значением k.
Значит, квадраты факторов преобразуются
