Понятие моделирующего алгоритма и формализованной схемы процесса
Для имитационного моделирования процесса на ЭВМ необходимо преобразовать его математическую модель в специальный моделирующий алгоритм, в соответствии с которым в ЭВМ будет вырабатываться информация, описывающая элементарные явления исследуемого процесса с учетом их связей и взаимных влияний. Определенная часть циркулирующей информации выводится "на печать" и используется для определения тех характеристик процесса, которые требуется получить в результате моделирования (рис. 4.1).
Центральным звеном моделирующего алгоритма является собственно имитационная модель формализованная схема процесса. Формализованная схема представляет собой формальное описание процедуры функционирования сложного объекта в исследуемой операции и позволяет для любых задаваемых значений входных факторов модели (переменных –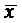 
, детерминированных – 
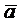, случайных – 
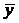) просчитать соответствующие им числовые значения выходных характеристик 
.
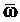Остальные модели (рис. 4.1) представляют собой внешнее математическое обеспечение процесса имитации.
Модели входов обеспечивают задание тех или иных значений входных факторов. Статические модели детерминированных входов элементарны: это массивы значений констант, соответствующих определенным факторам модели. Динамические модели входов обеспечивают изменение значений детерминированных факторов во времени по известному закону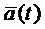 
.
Модели случайных входов (иначе – датчики случайных чисел) имитируют поступление на вход изучаемого объекта случайных воздействий с заданными (известными) законами распределения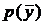 
. Динамические модели случайных входов учитывают, что законы распределения случайных величин являются функциями времени, т.е. для каждого периода времени либо форма, либо характеристика закона распределения (например, математическое ожидание, дисперсия и т.д.) будут своими.
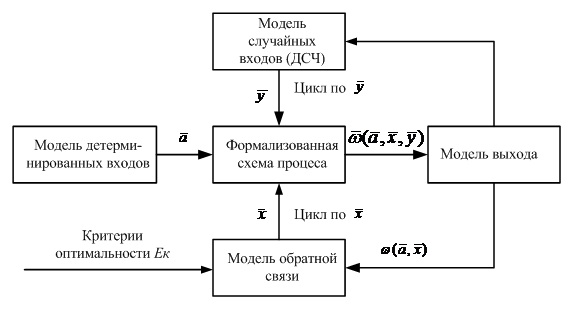
Рис. 4.1. Структура моделирующего алгоритма для оптимизационной модели со случайными факторами
В связи с тем, что результат, полученный при воспроизведении единственной реализации из-за наличия случайных факторов, не может характеризовать исследуемый процесс в целом, приходится анализировать большое число таких реализаций, так как только тогда по закону больших чисел получаемые оценки приобретают статистическую устойчивость и могут быть с определенной точностью приняты за оценки искомых величин. Модель выхода обеспечивает накопление, обработку и анализ полученного множества случайных результатов. Для этого с ее помощью организуется многократный просчет значений выходных характеристик при постоянных значениях факторов 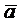, 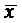и различных значениях случайных факторов 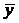(в соответствии с заданными законами распределения) – "цикл по у". В связи с этим модель выхода включает программы тактического планирования эксперимента на ЭВМ определение способа проведения каждой серии прогонов, соответствующей конкретным значениям 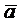и 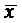. Кроме того, модель решает задачу обработки случайных значений выходных характеристик, в результате которой они очищаются от влияния случайных факторов и поступают на вход модели обратной связи, т.е. модель выхода реализует сведение стохастической задачи кдетерминированной методом “осреднения по результату”.
Модель обратной связи позволяет на основе анализа получаемых результатов моделирования изменять значения переменных управления, реализуя функцию стратегического планирования имитационно эксперимента. При использовании методов теории оптимального планирования эксперимента одной из функций модели обратной связи является представление результатов моделирования в аналитическом виде – определение уравнений функции отклика (или характеристической поверхности). При оптимизации модель выхода вычисляет наоснове значений выходных характеристик 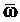значение целевой функции f( 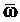)и с помощью того или иного численного метода оптимизации изменяет значения переменных управления для выбора значений наилучших с точки зрения целевой функции.