Классификация численных методов

Численные методы условно разбиваются на следующие классы:

1) методы нулевого порядка (не требуют использования производных функций, участвующих в задаче);

2) методы первого порядка (требуют использования производных первого порядка);

3) методы второго порядка (требуют использования производных второго и более высокого порядков).

Алгоритмы численных методов решения задач математического программирования

Рассмотрим несколько классических численных методов решения задач математического программирования (ЗМП) без ограничений

.[3] (5.1)

Идеи, лежащие в основе этих методов, могут быть использованы для построения аналогичных методов решения ЗМП с ограничениями.

5.3.1. Метод наискорейшего спуска (подъема)

Метод предназначен для решения задачи (5.1) и принадлежит классу методов первого порядка. Метод основан на том факте, что градиент 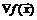целевой функции указывает направление ее максимального возрастания.

Описание алгоритма

Шаг 0. Выбирается точка начального приближения 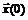, параметр длины шага 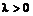, параметр дробления шага 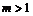и точность решения .

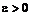Шаг k. На k-м шаге пересчет приближений производится по формулам

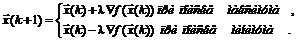(5.2)

Если при этом происходит «переход» через точку экстремума, то есть оказываются справедливыми неравенства

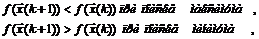
то длина шага уменьшается в m раз.

Критерием останова алгоритма является неравенство

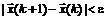. (5.3)

Алгоритм завершает свою работу, как только выполнится (5.3). В качестве решения исходной задачи берется последнее полученное приближение .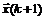

На рис. 5.1 показана схема реализации метода наискорейшего спуска при поиске минимума выпуклой функции одной переменной.

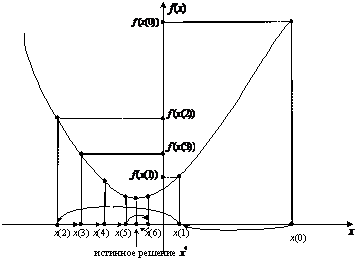
Рис. 5.1

Метод сопряженных градиентов

Метод предназначен для решения задачи (5.1) и принадлежит классу методов первого порядка. Метод представляет собой модификацию метода наискорейшего спуска (подъема) и автоматически учитывает особенности целевой функции, ускоряя сходимость.

Описание алгоритма

Шаг 0. Выбирается точка начального приближения 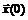, параметр длины шага 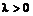, точность решения 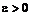и вычисляется начальное направление поиска .

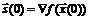Шаг k. На k-м шаге находится минимум (максимум) целевой функции на прямой, проведенной из точки 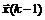по направлению 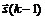. Найденная точка минимума (максимума) определяет очередное k-е приближение 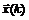, после чего определяется направление поиска

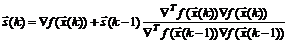. (5.4)

Формула (5.4) может быть переписана в эквивалентном виде

.

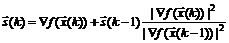Алгоритм завершает свою работу, как только выполнится условие 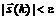; в качестве решения принимается значение последнего полученного приближения .

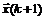Метод Ньютона

Метод предназначен для решения задачи (5.1) и принадлежит классу методов второго порядка. В основе метода лежит разложение Тейлора целевой функции и то, что в точке экстремума 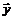градиент функции равен нулю, то есть .

Действительно, пусть некоторая точка 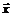лежит достаточно близко к точке искомого экстремума 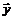. Рассмотрим i-ю компоненту градиента целевой функции и разложим ее в точке 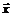по формуле Тейлора с точностью до производных первого порядка:

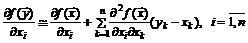. (5.5)

Формулу (5.5) перепишем в матричной форме, учитывая при этом, что :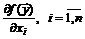

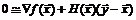, (5.6)

где 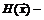матрица Гессе целевой функции в точке .

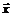Предположим, что матрица Гессе 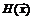невырождена. Тогда она имеет обратную матрицу 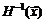. Умножая обе части уравнения (5.6) на 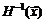слева, получим 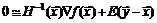, откуда

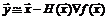. (5.7)

Формула (5.7) определяет алгоритм метода Ньютона: пересчет приближений на k-й итерации выполняется в соответствии с формулой

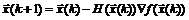. (5.8)

Алгоритм заканчивает свою работу, как только выполнится условие

,

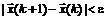где 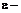заданная точность решения; в качестве решения принимается значение последнего полученного приближения .

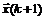Метод Ньютона-Рафсона

Метод является методом первого порядка и предназначен для решения систем n нелинейных уравнений c n неизвестными:

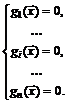
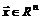(5.9)

В частности, этот метод может быть применен при поиске стационарных точек целевой функции задачи (5.1), когда необходимо решить систему уравнений из условия .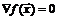

Пусть точка 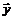есть решение системы (5.9), а точка 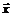расположена вблизи 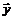. Разлагая функцию 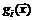в точке 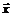по формуле Тейлора, имеем

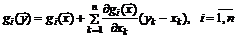, (5.10)

откуда (по условию 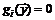) вытекает

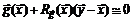, (5.11)

где 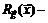матрица Якоби вектор-функции 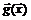. Предположим, что матрица Якоби 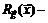невырождена. Тогда она имеет обратную матрицу 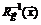. Умножая обе части уравнения (5.11) на 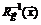слева, получим 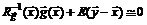, откуда

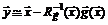. (5.12)

Формула (5.12) определяет алгоритм метода Ньютона-Рафсона: пересчет приближений на k-й итерации выполняется в соответствии с формулой

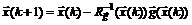. (5.13)

В случае одной переменной, когда система (5.9) вырождается в единственное уравнение 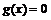, формула (5.13) принимает вид

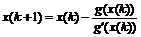, (5.14)

где 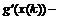значение производной функции 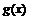в точке .

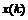На рис. 5.2 показана схема реализации метода Ньютона-Рафсона при поиске решения уравнения .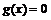

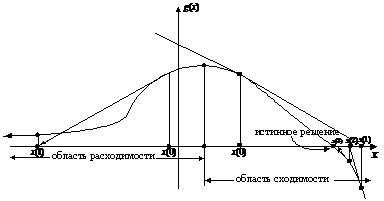
Рис. 5.2

Замечание 5.1. Сходимость численных методов, как правило, сильно зависит от начального приближения.

Замечание 5.2. Методы Ньютона и Ньютона-Рафсона требуют большого объема вычислений (надо на каждом шаге вычислять и обращать матрицы Гессе и Якоби).

Замечание 5.3. При использовании методов обязательно следует учитывать возможность наличия многих экстремумов у целевой функции (свойство мультимодальности).

ЛИТЕРАТУРА

1. Афанасьев М.Ю., Суворов Б.П. Исследование операций в экономике: Учебное пособие. – М.: Экономический факультет МГУ, ТЕИС, 2003 – 312 с.

2. Базара М, Шетти К. Нелинейное программирование. Теория и алгоритмы: Пер. с англ. – М.: Мир, 1982 – 583 с.

3. Берман Г.Н. Сборник задач по курсу математического анализа: Учебное пособие для вузов. – СПб: «Специальная Литература», 1998. – 446 с.

4. Вагнер Г. Основы исследования операций: В 3-х томах. Пер. с англ. – М.: Мир, 1972. – 336 с.

5. Вентцель Е.С. Исследование операций. Задачи, принципы, методология – М.: Наука, 1988. – 208 с.

6. Демидович Б.П. Сборник задач и упражнений по математическому анализу. – М.: Наука, 1977. – 528 с.

7. Дегтярев Ю.И. Исследование операций. – М.: Высш. шк., 1986. – 320 с.

8. Нуреев Р.М. Сборник задач по микроэкономике. – М.: НОРМА, 2006. – 432 с.

9. Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике: Учебник: В 2-х ч. – М.:Финансы и статистика, 1999. – 224 с.

10. Таха Х. Введение в исследование операций, 6-е изд.: Пер. с англ. – М.: Издательский дом «Вильямс», 2001. – 912 с.

11. Химмельблау Д. Прикладное нелинейное программирование: Пер. с англ. – М.: Мир, 1975 – 534 с.

12. Шикин Е.В., Шикина Г.Е. Исследование операций: Учебник – М.: ТК Велби, Изд-во Проспект, 2006. – 280 с.

13. Исследование операций в экономике: Учебн. пособие для вузов/ Н.Ш.Кремер, Б.А.Путко, И.М.Тришин, М.Н.Фридман; Под ред. проф. Н.Ш.Кремера. – М.: Банки и биржи, ЮНИТИ, 1997. – 407 с.

14. Матрицы и векторы: Учебн. пособие/ Рюмкин В.И. – Томск: ТГУ, 1999. – 40 с.

15. Системы линейных уравнений: Учебн. пособие / Рюмкин В.И. – Томск: ТГУ, 2000. – 45 с.

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ……………………………………...................................
1. ОСНОВЫ МАТЕМАТИЧЕСКОГО ПРОГРАММИРОВАНИЯ………………...
1.1. Постановка задачи математического программирования...............................
1.2. Разновидности ЗМП…………….…………..........................................
1.3. Базовые понятия математического программирования ................................
1.4. Производная по направлению. Градиент………….........................................
1.5. Касательные гиперплоскости и нормали…………..........................................
1.6. Разложение Тейлора……………………………...............................................
1.7. ЗНЛП и условия существования ее решения...................................................
1.8. Задачи ……………..……...................................................................................
2. РЕШЕНИЕ ЗАДАЧИ НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ БЕЗ ОГРАНИЧЕНИЙ................................................................................................................
2.1. Необходимые условия решения ЗНЛП без ограничений...............................
2.2. Достаточные условия решения ЗНЛП без ограничений.................................
2.3. Классический метод решения ЗНЛП без ограничений...................................
2.4. Задачи……………..............................................................................................
3. РЕШЕНИЕ ЗАДАЧИ НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ ПРИ ОГРАНИЧЕНИЯХ-РАВЕНСТВАХ.................................................................................
3.1. Метод множителей Лагранжа…………………………...................................
3.1.1. Назначение и обоснование метода множителей Лагранжа……………
3.1.2. Схема реализации метода множителей Лагранжа……………………...
3.1.3. Интерпретация множителей Лагранжа…………………………………
3.2. Метод подстановки…………………………….................................................
3.3. Задачи…………………………..........................................................................
4. РЕШЕНИЕ ЗАДАЧИ НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ ПРИ ОГРАНИЧЕНИЯХ-НЕРАВЕНСТВАХ………………………………………………..
4.1. Обобщенный метод множителей Лагранжа…………………………………
4.2. Условия Куна-Таккера…………………………..............................................
4.2.1. Необходимость условий Куна-Таккера…………………………………
4.2.2. Достаточность условий Куна-Таккера…………………………………..
4.2.3. Метод Куна-Таккера………………………...............................................
4.3. Задачи…………………………..........................................................................
5. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧИ НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ …………………………...……………………………………
5.1. Понятие алгоритма…………………………....................................................
5.2. Классификация численных методов…………………………………………
5.3. Алгоритмы численных методов……………………………………………...
5.3.1. Метод наискорейшего спуска (подъема)…………………………………
5.3.2. Метод сопряженных градиентов………………………….........................
5.3.3. Метод Ньютона………………………….....................................................
5.3.4. Метод Ньютона-Рафсона………………………………………………...
ЛИТЕРАТУРА………………………………..............................................................

[1] Определения линейной и нелинейной функций см. в разделе 1.2

[2] Крейсерской скоростью называется скорость, при которой расход топлива на единицу пути минимален.

[3] Выражение (5.1) означает «найти максимум (и (или) минимум) функции ».