Анализ чувствительности решений.

Решения, принимаемые при помощи «дерева», зависят от вероятностей исходов. При каких изменениях вероятностей решения изменятся?

Проведем анализ чувствительности решения, полученного в примере

5, причем рассмотрим изменение только вероятности благоприятного прогноза состояния рынка р (на данный момент р=0.45).

ОДО10=р×116400+(1 – р)×12400.

Приравнивая ОДО10 (с учетом стоимости затрат на обследование) к ОДО3

получаем

р×116400+(1 – р)×12400 – 10000=40000,

откуда р=0.36. Следовательно, если вероятность прогноза благоприятного состояния рынка будет меньше 0.36, то обращаться к экспертам нецелесообразно, т.е. первоначальное решение будет заменено на альтернативное.

Полный анализ чувствительности включает рассмотрение допустимых диапазонов изменения для вероятностей всех остальных исходов.

Парадокс Алле.

Рассмотрим две лотереи (рис. 4).

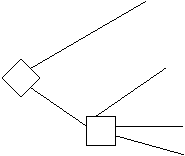
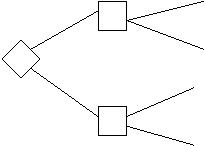1 млн С 0.1 5 млн

А 0.9

0.1 5 млн

В D 0.11 1 млн

0.89

1 млн

0.01 0 0.89 0

Рис. 4. Дерево решений двух лотерей

Примем значение функции полезности U(5 млн)=100, U(0)=0 и пусть

U(1 млн)= U.

В левой лотерее подавляющее большинство людей (не склонных к авантюризму) предпочитает альтернативу А (получить 1 млн. без риска) альтернативе В (принять участие в лотерее, где есть вероятность ничего не выиграть), т.е. полезность альтернативы А оценивается выше, чем полезность альтернативы В. Следовательно,

U > 0.1×100+0.89×U, откуда U > 10/0.11.

В правой лотерее подавляющее большинство людей предпочитает альтернативу С (почти та же вероятность выиграть, что и в D, но выигрыш существенно больше). Значит

0.1×100 > 0.11×U, откуда U < 10/0.11.

Мы видим, что в данном случае люди поступают не в соответствии с функцией полезности.

Рассмотрим еще один пример двух лотерей (рис. 5).

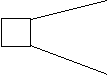
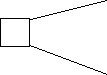0.6 50 0.5 44

0.4 – 20 0.5 0

Рис. 5. Сравнение двух лотерей

Ожидаемая денежная оценка обеих лотерей одинаковая

(0.6×50 – 0.4×20=0.5×44=22),

однако предъявление различным группам людей этих пар лотерей показало, что люди предпочитают правую лотерею, где риск проигрыша исключен.

Вышеприведенные примеры показывают огромную роль лица,

принимающего решение (ЛПР), его опытность, отношение к риску и т.п.

Нерациональное поведение.

Принятие решения ЛПР не в соответствии с максимизацией ожидаемой полезности будем называть нерациональным поведением.

Причины отклонения поведения людей от рационального связаны не только с их личностными качествами, но и с формулировкой альтернатив. Рассмотрим пример «дилемма генерала».

Есть две возможные дороги для вывода войск (600 чел.) из окружения,

данные о возможных исходах потерь людей представлены на рис. 6.

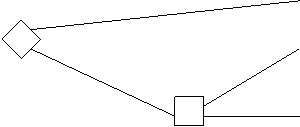Дорога 1 400 чел. погибнут

Дорога 2

1/3

Никто не погибнет

2/3 Все 600 чел. погибнут

Рис. 6. Дилемма генерала (исходы в виде потерь)

Большинство людей, рассматривающих данную дилемму, выбирают первую дорогу, стараясь избежать исхода, когда погибает весь отряд.

Но эта же дилемма была представлена испытуемым в виде исходов спасения людей (рис. 7).

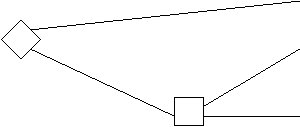Дорога 1 200 чел. спасены

Дорога 2

1/3

Все 600 чел. спасены

2/3 0 чел. спасены

Рис. 7. Дилемма генерала (исходы в виде спасения людей)

Теперь уже большинство испытуемых людей выбирают вторую дорогу,

так как на ней с вероятностью 1/3 можно спасти весь отряд.

Легко видеть, что деревья на рис. 6 и 7 эквивалентны, но одно представлено в виде потерь, а другое – в виде выигрышей.

Причины нерационального поведения:

• Суждение по представительности. Люди часто судят о

вероятности того, что объект А принадлежит к классу В только по похожести А на типовой объект класса В. При этом не учитываются количественные характеристики (возможные объемы наличия объектов А в классе В, размер выборки, по которой выносится суждение и т.п.).

• Суждение по встречаемости. Люди часто определяют вероятности

событий по тому, как часто они сами сталкиваются с этими событиями и насколько важными для них были эти встречи. Собственный опыт для большинства людей важней «закона больших чисел».

• Суждение по точке отсчета. Если при определении вероятностей

используется начальная информация (задаются некоторые оценки вероятностей), то она существенно влияет на результат, начальная оценка

«давит» на суждение.

• Сверхдоверие. Люди чрезмерно доверяют своим суждениям,

особенно о прошлых явлениях. Эксперименты показали, что люди переоценивали свои суждения о вероятностях редких явлений природы, о вероятностях резких изменений курса акций на бирже и т.п.

• Стремление к исключению риска. Люди соглашаются на средние (и

хуже средних) альтернативы, только чтобы не возникли ситуации, где хотя бы при очень малых вероятностях возможны большие потери.

Перечисленные выше субъективные причины имеют личностный характер и вытекают из более общих объективных обстоятельств:

• недостаток информации у ЛПР в процессе выбора;

• недостаточный опыт ЛПР;

• ЛПР ищет решение, оптимальное с точки зрения совокупности

критериев, упорядоченных по важности, но не может его найти;

• различие между объективно требуемым временем для реализации

планов и субъективным горизонтом планирования ЛПР.

Знание причин нерационального поведения позволяет более точно выявить предпочтение потребителей. Особое значение следует придавать форме постановки вопросов, возможности влияния точки отсчета, фактора сверхуверенности и т.д.