Алгебраический симплексный метод. Основные положения данного метода.
Алгебраический симплексный метод. Основные положения данного метода.
Симплексный метод- это метод целенаправленного перебора опорных решений задачи, который позволяет ха конечное число шагов, либо найти оптимальное решение, либо установить, что оптимальное решение не существует.
Основное содержание симплексного метода состоит в следующем:
1. Необходимо указать способ нахождения начального опорного решения.
2. Следует указать способ перехода от одного опорного решения к другому, причем переход должен осуществляется к более оптимального или по по крайней мере не существующему решению.
3. Требуется задать критерий, который позволяет своевременно прекратить перебор решений, остановивших на оптимальном или сделать заключение , что оптимального решения нет.
Свое название симплексный метод получил от простых областей допустимых решений, которые рассматривались на ранних этапах разработки метода.
10. Алгоритм решение задачи симплексным методом(первый опорный план)
Рассмотрим алгоритм симплексного метода на примере задачи линейного программирования. Система ограничений, которой содержит неравенство вида <=
I. Приведем задачу к канонической форме. Введем m дополнительных неотрицательных переменных
х n+1; x n+2 ….. x n+m
в результате получим:
F( X)= c1 x1+ c2x2+….a1nxn +cnxn +0*xn+1 +0*xn+2 + ……+0*xm+n
Система
2.найдем начальное опорное решение. Выпишем матрицу из коэффициентов полученной системы ограничений
Матрица
Коэффициенты при дополнительных переменных образуют единичную диагональную матрицу- базис, поэтому x n+1, x n+2…..x n+m называют базисными переменными.
Выразим базисные переменные через основные:
X n+1=b1-a11x1-a12x2-……-a m x n
X n+2=b2-a1x1-a22x2-……-a2m x n
…………………………………..
X m+ n=bm-am1x1-am2x2-…..-a m n x n
Прировняем к 0 основные переменные: x1=x2=….=x n=0
Тогда: xn+1=b1
Xn+2=b2
…………
X m +n=b m
В результате получаем начальное опорное решение
X1= (0; 0;….;0; b1; b2…..b m)
Занесем начальное опорное решение, базисные переменные, коэффициенты системы ограничений в специальную симплексную таблицу.
3.Проверка плана на оптимальность. При решении задачи на max опорный план считается оптимальным; если все коэффициенты индексной строки неотрицательны.
Если хотя бы один элемент отрицателен, то план считается неоптимальным ( т.е. – оптимальный; + неоптимальный)
При решении задачи на min, план считается оптимальным если все коэффициенты индексной строки не положительны.
Если план оказался оптимальным, то задача решена, необходимо выписать ответ, проанализировать его и сделать вывод о количестве оптимальных решений.
Если же план не оптимальный, то решение задачи продолжается т.е. переходим к др. пункту.
11. Алгоритм решения задачи симплексным методом ( проверка на оптимальность, определения ведущего столбца и строки, построение нового опорного плана).
Проверка плана на оптимальность. При решении задачи на max опорный план считается оптимальным; если все коэффициенты индексной строки неотрицательны.
Если хотя бы один элемент отрицателен, то план считается неоптимальным ( т.е. – оптимальный; + неоптимальный)
При решении задачи на min, план считается оптимальным если все коэффициенты индексной строки не положительны.
Если план оказался оптимальным, то задача решена, необходимо выписать ответ, проанализировать его и сделать вывод о количестве оптимальных решений.
Если же план не оптимальный, то решение задачи продолжается т.е. переходим к др. пункту.
Определение ведущего столбца. При решении задачи на max из всех отрицательных элементов индексной строки выбираем наибольший по модулю, этот элемент и определяет ведущий столбец.
Определение ведущей строки. Элементы столбца ЗБП делим на соответствующие элементы ведущего столбца, а результаты заносим в последний столбец таблицы.
Замечание. Делить можно числа только одного знака (+/+;-/-) т.е. в последнем столбце таблицы должны получаться только положительные значения. Если встретились числа разных знаков или деление на 0, то в столбце на соответствующем месте ставится прочерк.
Из всех элементов последнего столбца выбираем наименьший, он и определяет ведущую строку.
Определение разрешающего элемента. Разрешающий элемент находится на пересечении ведущей строки и ведущего столбца.
Заполнение нового опорного плана. В первую очередь заполняется столбец БП (базисные переменные). Базисная переменная, которая в старом плане
Оказалась на ведущей строке, покидает базис, ее место занимает переменная из ведущего столбца, а остальные переменные свое место в базисе сохраняют.
Далее заполняем строку, которая в старом плане была ведущей, для этого элементы старой ведущей строки делим на разрешающий элемент, а результаты заносим в новый план на соответствующее место.
В результате деления на месте старого разрешающего элемента окажется единица. Остальные элементы старого ведущего столбца в новом плане обнуляем. Все остальные элементы нового плана рассчитываются по формуле:
Элемент нового плана = элемент старого плана-(произведение дополняющих элементов до прямоугольника)/разрешающий элемент
Получив новый план проверяем его на оптимальность. Алгоритм повторяется до тех пор пока не получим оптимальное решение.
13. Анализ оптимального плана симплексного метода на примере задачи планирования товарооборота.
Оптимальное решение выписывают из столбца ЗБП последнего оптимального плана симплексной таблицы. Если какая либо переменная в этом столбце отсутствует, то в оптимальном плане она равна 0.
Значение целевой функции также берется из столбца ЗБП последнего оптимального плана. Оптимальный вектор переменных обозначаем X*, а оптимальное значение целевой функции F max(X*)
При решении задачи планирования товарооборота( задача о распределе6нии ресурсов), основные переменные указывают на количество реализуемой продукции каждого вида, для получения max дохода. А дополнительные переменные указывают на количество недоиспользованных ресурсов каждого вида. Если какая нибудь дополнительная переменная равна 0, то соответствующий ей ресурс использован полностью и является дефицитным. Положительное значение дополнительной переменной говорит о имеющихся излишках ресурсов.
Нулевое значение какой-либо основной переменной говорит о том, что соответствующий товар невыгоден, его реализация нерентабельна.
Вывод о количестве оптимальных решений можно сделать по индексной строке оптимального плана. Если в индексной строке 0 соответствуют только столбцам базисных переменных, то полученное оптимальное решение единственно. Если 0 соответствует небазисной переменной, то задача будет иметь альтернативный оптимум.
Альтернативный оптимум можно найти, если принять за ведущий столбец, столбец с небазисным 0. При этом среди элементов данного столбца должен быть один положительный.
Если известны два оптимальных решения, то в задачи с альтернативным оптимумом можно записать бесконечное множество оптимальных решений, но все они будут линейными комбинациями найденных оптимальных решений.
Xопт =t *X*+ (1-t)X**
X*- первое оптимальное решение
X**- второе оптимальное решение
0 
t 1
Если в ходе решения в ведущем столбце все коэффициенты aij оказались <=0, то целевая функция F(X)- неограниченна на множестве допустимых решений. А значит, оптимального решения задача не имеет.
Если в ходе последнем столбце симплексной таблицы оказалось сразу несколько одинаковых наименьших элементов, то опорный план считается вырожденным, а дальнейшие решения может привести к зацикливанию. Для определения ведущей строки в данном случае применяется метод Креко: рассматривают все строки претендующие на ведущую, в каждой из них находят предполагаемый разрешающий элемент. Элементы каждой строки делят на свой разрешающий элемент, а результаты записывают в дополнительные строки симплексной таблицы.
Дополнительные строки сравнивают между собой двигаясь слева на право по столбцам, сравнение проводят до тех пор пока не встретится наименьший элемент. Он и определит ведущую строку в рассматриваемом плане.
14. Метод искусственного базиса на примере системы ограничений, содержащей уравнения.
Заметим что классический симплексный метод основывается на задаче с системой ограничений вида <=, на первом шаге такой задачи ее условий приводятся к канонической форме. Тем самым образуется базис для построения начального решения.
Если задача сразу представлена в канонической форме, то в ней как правило отсутствуют переменные выполняющие роль базисных. Введение же дополнительных переменных нарушит каноническую форму и не позволит реализовать алгоритм симплексного метода. В этом случае прибегают к методу искусственного базиса.
F(X)=c1x1+c2x2+…..+cnxn 
extr
A11x1+a12x2+….+a1nxn=b1
A21x1+a22x2+….+a2nxn=b2
…………………………
Am1x1+am2x2+….+amnxn=bm
xj 
0; j=1,n
введем m- искусственных переменных yi=0;i=1,m. каждая искусственная переменная вводится только в одно уравнение системы, и так как они заведомо равны 0, то знак равенства не изменяется
A11x1+a12x2+….+a1nxn+y1=b1
A21x1+a22x2+….+a2nxn+y2=b2
…………………………
Am1x1+am2x2+….+amnxn+ym=bm
xj 0; j=1,n
y i0; i=1,m
Использование искусственных переменных в системе ограничений приводит к тому, что на целевую функцию накладывается так называемый штраф в виде бесконечно большой положительной величины, точное значение которой не задается, а используется обозначение М. При решении задачи на min целевая функция примет вид:
F(X)=c1x1+c2x2+…..+cnxn+My1+My2+….+Mym min
При решении задачи на max целевая функция примет вид:
F(X)=c1x1+c2x2+…..+cnxn+My1+My2+….+Mym max
Дальнейшее решение будет протекать по следующим этапам:
1. Необходимо выразить искусственные переменные через основные
2. Полученные выражения подставить в целевую функцию
3. Выполнить тождественное преобразование целевой функции ( раскрыт скобки, привести подобные)
4. В результате целевая функция будет содержать только основные переменные, но коэффициенты при них будут содержать штрафы М
5. Для преобразования целевой функции и преобразованной системы ограничений находим начальное опорное решение, обычным симплексным методом
Заметим, что в результате преобразования целевой функции появляется свободный член, а значит, первоначальное значение целевой функции будет отлично от 0.
6. Дальнейшее решение продолжаем по алгоритму классического симплексного метода. На каждом шаге нужно стараться исключить искусственные переменные из базисных. В отличном от решении должны статься только основные переменные.
Причем их значение должны освободиться от штрафа М. Штрафы останутся только в индексной строке искусственных переменных.
16.рОсновные теоремы линейного программирования. Теоремы об оптимальном решении в ограниченной и неограниченной области.
Базисным(опорным) решением системы m –линейных уравнений с n –переменными называется решением в котором все (n-m) неосновных переменных равны нулю.
Число базисных решений является конечным, так как оно равно числу групп основных переменных, не превосходящему
Теорема.Если задача ЛП имеет оптимальное решение, то линейная функция, принимает максимальное значение в одной из угловых точек многогранника решений. Если линейная функция принимает максимальное значение более чем в одной угловой точке, являющейся выпуклой линейной композицией этих точек.
Графы состояний СМО.
При анализе случайных процессов с дискретными состояниями и непрерывным временем удобно пользоваться вариантом схематичного изображения возможных состояний СМО (рис. 6.2.1) в виде графа с разметкой его возможных фиксированных состояний. Состояния СМО изображаются обычно либо прямоугольниками, либо кружками, а возможные направления переходов из одного состояния в другое ориентированы стрелками, соединяющими эти состояния. Например, размеченный граф состояний одноканальной системы случайного процесса обслуживания в газетном киоске приведен на рис. 6.2.1.
Система может находиться в одном из трех состояний: S0 – канал свободен, простаивает, Si – канал занят обслуживанием, S2 — канал занят обслуживанием и одна заявка в очереди. Переход системы из состояния SQ В SI происходит под воздействием простейшего потока заявок интенсивностью l01, а из состояния Si в состояние 5* 0 систему переводит поток обслуживания с интенсивностью l10. Граф состояний системы обслуживания с проставленными интенсивностями потоков у стрелок называется размеченным. Поскольку пребывание системы в том или ином состоянии носит вероятностный характер, то вероятность pi(t) того, что система будет находиться в состоянии Si в момент времени t, называется вероятностью i-го состояния СМО и определяется числом поступивших заявок k на обслуживание.
Цепи Маркова.
Вопрос 55. Цепи Маркова.
Простейший Пуассоновкий поток является самым простым с точки зрения его матричного описания, а вот регулярный поток не смотря на простоту физического описания простейшим не является. И для его описания нужен сложный матричный аппарат.
Интенсивностью или средней плотностьюпотока, наз-ся среднее число событий потока, наступающих в ед времени причем эта ед выбирается от масштаба и характеристики потока событий.
Полезная роль простейшего потока состоит в том, что суммарный поток образуемый взаимным наложением достаточно большого числа сравнимых по интенсивности потоков, каждый из которых обладает свойством стационарности, ординарности и отсутствием последствий можно приближенно считать простейшим и приближение будет тем точнее, чем больше число слагаемых потоков.
Уравнения Колмогорова.
Рассмотрим математическое описание марковского случайного процесса с дискретными состояниями системы S0, S1, S2 (см. рис. 6.2.1) и непрерывным временем. Полагаем, что все переходы системы массового обслуживания из состояния Si в состояние Sj происходят под воздействием простейших потоков событий с интенсивностями lij, а обратный переход — под воздействием другого потока lij, Введем обозначение рi как вероятность того, что в момент времени t система находится в состоянии Si. Для любого момента времени t справедливо записать нормировочное условие — сумма вероятностей всех состояний равна 1:
S pi(t) = p0(t) + p1(t) + p2(t) = 1.
i=0
Проведем анализ системы в момент времени t, задав малое приращение времени Dt, и найдем вероятность p1(t + Dt) того, что система в момент времени (t + Dt) будет находиться в состоянии S1, которое достигается разными вариантами:
а) система в момент t с вероятностью pi(t) находилась в состоянии Si и за малое приращение времени Dt так и не перешла в другое соседнее состояние — ни в S0, ни в S2. Вывести систему из состояния S1 можно суммарным простейшим потоком с интенсивностью (l10 + l12) , поскольку суперпозиция простейших потоков также является простейшим потоком. На этом основании вероятность выхода из состояния S1 за малый промежуток времени Dt приближенно равна (l10 + l12)×Dt. Тогда вероятность невыхода из этого состояния равна [1 — (l10 + l12) × Dt]. В соответствии с этим вероятность того, что система останется в состоянии S1 на основании теоремы умножения вероятностей, равна:
p1(t)[l – (l10 + l12)×Dt];
б) система находилась в соседнем состоянии S0 И за малое время Dt перешла в состояние S1. Переход системы происходит под воздействием потока l01 c вероятностью, приближенно равной l01 Dt.
Вероятность того, что система будет находиться в состоянии S1, в этом варианте равна p0(t) l01Dt;
в) система находилась в состоянии S2 и за время Dt перешла в состояние S1 под воздействием потока интенсивностью l21 с вероятностью, приближенно равной l21Dt. Вероятность того, что система будет находиться в состоянии S1, равна p2(t)l21Dt.
Применяя теорему сложения вероятностей для этих вариантов, получим выражение:
p1(t + Dt) = p1(t)[1 – (l10 + l12 ) Dt] + p0(t) l01Dt + p2(t)l21Dt,
которое можно записать иначе:
p1(t + Dt) – p1(t) = p0(t)l01 + p2(t)l21 – p1(t)(l10 + l12).
Dt
Переходя к пределу при А/ -^ О, приближенные равенства перейдут в точные, и тогда получим производную первого порядка
dp1 = p0l01 + p2l21 – p1(l10 + l12),
dt
что является дифференциальным уравнением.
Проводя рассуждения аналогичным образом для всех других состояний системы, получим систему дифференциальных уравнений, которые называются уравнениями А.Н. Колмогорова:
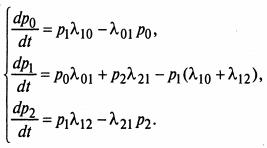
Для составления уравнений Колмогорова существуют общие правила.
Уравнения Колмогорова позволяют вычислить все вероятности состояний СМО Si в функции времени pi(t). В теории случайных процессов показано, что если число состояний системы конечно, а из каждого из них можно перейти в любое другое состояние, то существуют предельные (финальные) вероятности состояний, которые показывают на среднюю относительную величину времени пребывания системы в этом состоянии. Если предельная вероятность состояния S0 равна p0 = 0,2, то, следовательно, в среднем 20% времени, или 1/5 рабочего времени, система находится в состоянии S0. Например, при отсутствии заявок на обслуживание k = 0, p0 = 0,2, следовательно, в среднем 2 ч в день система находится в состоянии S0 и простаивает, если продолжительность рабочего дня составляет 10 ч.
Поскольку предельные вероятности системы постоянны, то, заменив в уравнениях Колмогорова соответствующие производные нулевыми значениями, получим систему линейных алгебраических уравнений, описывающих стационарный режим СМО. Такую систему уравнений составляют по размеченному графу состояний СМО по следующим правилам: слева от знака равенства в уравнении стоит предельная вероятность рi рассматриваемого состояния S1 умноженная на суммарную интенсивность всех потоков, выводящих (выходящие стрелки) из данного состояния Si систему, а справа от знака равенства — сумма произведений интенсивности всех потоков, входящих (входящие стрелки) в состояние Si систему, на вероятность тех состояний, из которых эти потоки исходят. Для решения подобной системы необходимо добавить еще одно уравнение, определяющее нормировочное условие, поскольку сумма вероятностей всех состояний СМО равна 1:
S pi(t)=1
i=1
Например, для СМО, имеющей размеченный граф из трех состояний S0, S1, S2 рис. 6.2.1, система уравнений Колмогорова, составленная на основе изложенного правила, имеет следующий вид:
Выходящие Входящие
Для состояния S0® p0 – l01 = p1×l10
Для состояния S1® (l10 + l12) = p0l01 + p1l21
Для состояния S2® p2l21 = p1l12
p0 + p1 + p2 = 1
Пример 1. Составим систему уравнений Колмогорова в общем виде для случая, когда граф состояний имеет вид (рис. 6.2.2):
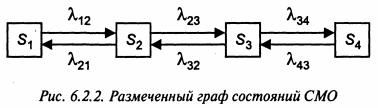
Плотность вероятностей этих переходов указана рядом с соответствующими стрелками. Пользуясь приведенными выше правилами, получаем систему уравнений:
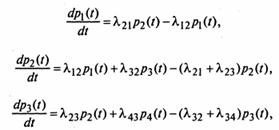
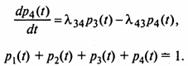
К этим уравнениям надо добавить еще начальные условия. Например, если при t = 0 система S находится в состоянии S1, то начальные условия можно записать так:
p1(0) = 1, p2(0) = p3(0) = p4(0) = 0.
Переходы между состояниями СМО происходят под воздействием поступления заявок и их обслуживания. Вероятность перехода в случае, если поток событий простейший, определяется вероятностью появления события в течение времени Dt, т.е. величиной элемента вероятности перехода lij Dt, где lij — интенсивность потока событий, переводящих систему из состояния / в состояние j (по соответствующей стрелке на графе состояний).
Если все потоки событий, переводящие систему из одного состояния в другое, простейшие, то процесс, протекающий в системе, будет марковским случайным процессом, т.е. процессом без последствия. В этом случае поведение системы достаточно просто определяется, если известны интенсивность всех этих простейших потоков событий. Например, если в системе протекает марковский случайный процесс с непрерывным временем, то, записав систему уравнений Колмогорова для вероятностей состояний и проинтегрировав эту систему при заданных начальных условиях, получим все вероятности состояний как функции времени:
pi(t), p2(t), …, pn(t).
Во многих случаях на практике оказывается, что вероятности состояний как функции времени ведут себя таким образом, что существует
Lim pi(t) = pi (i = 1,2, …, n)
t®¥
независимо от вида начальных условий. В этом случае говорят, что существуют предельные вероятности состояний системы при t®¥ и в системе устанавливается некоторый предельный стационарный режим. При этом система случайным образом меняет свои состояния, но каждое из этих состояний осуществляется с некоторой постоянной вероятностью, определяемой средним временем пребывания системы в каждом из состояний.
Вычислить предельные вероятности состояния pi можно, если в системе положить все производные равными 0, поскольку в уравнениях Колмогорова при t®¥ зависимость от времени пропадает. Тогда система дифференциальных уравнений превращается в систему обычных линейных алгебраических уравнений, которая совместно с нормировочным условием позволяет вычислить все предельные вероятности состояний.
Пример 2. Запишем систему алгебраических уравнений для вычисления предельных вероятностей состояний системы, изображенной на рис. 6.2.2.
Для этого допустим, что
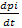= 0 (i = 1; 2; 3; 4),
тогда из записанной ранее в примере 1 системы уравнений Колмогорова получаем:
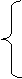l21p23 - l12p1 =0,
l12p1 + l23p^3 - (l21 + l23)p2 =0,
l23p2 + l43p4 -(l32 +l34)p3 =0,
l34p3 - l43p4=0;
И, Кроме того, мы должны учесть нормировочное условие:
p1+p2+p3+p4=1
Любое из уравнений записанной системы можно исключить, использовав вместо него нормировочное условие.
Вопрос 58. Классификация СМО в коммерческой деятельности (по числу каналов, по характеру расположения, по характеристике каналов).
По числу каналовобслуживания СМО разделяются наодноканальныел = 1 и многоканальные, для которых л > 2. Одноканальные например: выполняемые на рабочем месте операции одним бухгалтером, менеджером, коммерсантом, товароведом, экономистом, торговым аппаратом. В зависимости отвзаимного расположения каналовсистемы подразделяются на СМО спараллельными и с последовательными каналами.В СМО с параллельными каналами входной поток заявок на обслуживание является общим, и поэтому заявки в очереди могут обслуживаться любым свободным каналом, например официантами в ресторане. В таких СМО очередь на обслуживание можно рассматривать как общую. В СМО с последовательным расположением каналов каждый канал может рассматриваться как отдельная одноканальная СМО или фаза обслуживания. Очевидно, выходной поток обслуженных заявок одной СМО является входным потоком для последующей СМО.
В зависимости отхарактеристик каналов обслуживаниямногоканальные СМО подразделяются на СМО соднородными и неоднородными каналами. Отличие состоит в том, что в СМО с однородными каналами заявка потока может обслуживаться любым свободным каналом, а в СМО с неоднородными каналами отдельные заявки обслуживаются только специально для этой
цели предназначенными каналами. В кафе, например, посетитель проходит несколько разных по своему содержанию операций обслуживания, каждая из которых может быть представлена в виде простейшей одноканальной СМО, называемой фазой обслуживания, а в целом весь процесс обслуживания только посетителей может быть представлен в виде структурной модели многофазной СМО.
Вопрос 59. Классификация СМО в коммерческой деятельности (по возможности образования очереди, по характеру очереди, по организации потока заявок, по характеру дисциплины).
СМО в зависимостиот возможности образования очередиподразделяются на два основных типа:СМО с отказамиобслуживания иСМО с ожиданием(очередью) обслуживания. В СМО с отказами возможен отказ в обслуживании, если все каналы уже
заняты обслуживанием, а образовывать очередь и ожидать обслуживание нельзя. В то же время СМО с ожиданием подразделяются на СМО снеограниченным ожиданием, или с неограниченной очередью ИЛИ временем ожидания и СМО сограниченными ожиданиями или очередью, в которых накладываются ограничения на максимально возможную длину очереди или на максимально возможное время пребывания заявки в очереди время работы системы.
Примерами СМО с ограничением на длину очереди: поступление товаров в подсобные помещения, емкости, вместимость которых, естественно, не беспредельна.
Примером СМО с ограничением на время ожидания является обслуживание скоропортящихся товаров, готовых блюд в производстве ресторана, кафе, плодоовощной продукции и продовольственных товаров.
В зависимостиот организации потока заявок СМО подразделяются наразомкнутые и замкнутые. В разомкнутых СМО выходной поток обслуженных заявок не связан с входным потоком заявок на обслуживание и имеет неограниченный источник заявок.
Примером такой системы в коммерческой деятельности является система обслуживания механиками торгового оборудования, которое через некоторое время после ремонта все же опять приходит в неисправное состояние и поступает с заявкой на обслуживание
Алгебраический симплексный метод. Основные положения данного метода.
Симплексный метод- это метод целенаправленного перебора опорных решений задачи, который позволяет ха конечное число шагов, либо найти оптимальное решение, либо установить, что оптимальное решение не существует.
Основное содержание симплексного метода состоит в следующем:
1. Необходимо указать способ нахождения начального опорного решения.
2. Следует указать способ перехода от одного опорного решения к другому, причем переход должен осуществляется к более оптимального или по по крайней мере не существующему решению.
3. Требуется задать критерий, который позволяет своевременно прекратить перебор решений, остановивших на оптимальном или сделать заключение , что оптимального решения нет.
Свое название симплексный метод получил от простых областей допустимых решений, которые рассматривались на ранних этапах разработки метода.
10. Алгоритм решение задачи симплексным методом(первый опорный план)
Рассмотрим алгоритм симплексного метода на примере задачи линейного программирования. Система ограничений, которой содержит неравенство вида <=
I. Приведем задачу к канонической форме. Введем m дополнительных неотрицательных переменных
х n+1; x n+2 ….. x n+m
в результате получим:
F( X)= c1 x1+ c2x2+….a1nxn +cnxn +0*xn+1 +0*xn+2 + ……+0*xm+n
Система
2.найдем начальное опорное решение. Выпишем матрицу из коэффициентов полученной системы ограничений
Матрица
Коэффициенты при дополнительных переменных образуют единичную диагональную матрицу- базис, поэтому x n+1, x n+2…..x n+m называют базисными переменными.
Выразим базисные переменные через основные:
X n+1=b1-a11x1-a12x2-……-a m x n
X n+2=b2-a1x1-a22x2-……-a2m x n
…………………………………..
X m+ n=bm-am1x1-am2x2-…..-a m n x n
Прировняем к 0 основные переменные: x1=x2=….=x n=0
Тогда: xn+1=b1
Xn+2=b2
…………
X m +n=b m
В результате получаем начальное опорное решение
X1= (0; 0;….;0; b1; b2…..b m)
Занесем начальное опорное решение, базисные переменные, коэффициенты системы ограничений в специальную симплексную таблицу.
3.Проверка плана на оптимальность. При решении задачи на max опорный план считается оптимальным; если все коэффициенты индексной строки неотрицательны.
Если хотя бы один элемент отрицателен, то план считается неоптимальным ( т.е. – оптимальный; + неоптимальный)
При решении задачи на min, план считается оптимальным если все коэффициенты индексной строки не положительны.
Если план оказался оптимальным, то задача решена, необходимо выписать ответ, проанализировать его и сделать вывод о количестве оптимальных решений.
Если же план не оптимальный, то решение задачи продолжается т.е. переходим к др. пункту.
11. Алгоритм решения задачи симплексным методом ( проверка на оптимальность, определения ведущего столбца и строки, построение нового опорного плана).
Проверка плана на оптимальность. При решении задачи на max опорный план считается оптимальным; если все коэффициенты индексной строки неотрицательны.
Если хотя бы один элемент отрицателен, то план считается неоптимальным ( т.е. – оптимальный; + неоптимальный)
При решении задачи на min, план считается оптимальным если все коэффициенты индексной строки не положительны.
Если план оказался оптимальным, то задача решена, необходимо выписать ответ, проанализировать его и сделать вывод о количестве оптимальных решений.
Если же план не оптимальный, то решение задачи продолжается т.е. переходим к др. пункту.
Определение ведущего столбца. При решении задачи на max из всех отрицательных элементов индексной строки выбираем наибольший по модулю, этот элемент и определяет ведущий столбец.
Определение ведущей строки. Элементы столбца ЗБП делим на соответствующие элементы ведущего столбца, а результаты заносим в последний столбец таблицы.
Замечание. Делить можно числа только одного знака (+/+;-/-) т.е. в последнем столбце таблицы должны получаться только положительные значения. Если встретились числа разных знаков или деление на 0, то в столбце на соответствующем месте ставится прочерк.
Из всех элементов последнего столбца выбираем наименьший, он и определяет ведущую строку.
Определение разрешающего элемента. Разрешающий элемент находится на пересечении ведущей строки и ведущего столбца.
Заполнение нового опорного плана. В первую очередь заполняется столбец БП (базисные переменные). Базисная переменная, которая в старом плане
Оказалась на ведущей строке, покидает базис, ее место занимает переменная из ведущего столбца, а остальные переменные свое место в базисе сохраняют.
Далее заполняем строку, которая в старом плане была ведущей, для этого элементы старой ведущей строки делим на разрешающий элемент, а результаты заносим в новый план на соответствующее место.
В результате деления на месте старого разрешающего элемента окажется единица. Остальные элементы старого ведущего столбца в новом плане обнуляем. Все остальные элементы нового плана рассчитываются по формуле:
Элемент нового плана = элемент старого плана-(произведение дополняющих элементов до прямоугольника)/разрешающий элемент
Получив новый план проверяем его на оптимальность. Алгоритм повторяется до тех пор пока не получим оптимальное решение.
13. Анализ оптимального плана симплексного метода на примере задачи планирования товарооборота.
Оптимальное решение выписывают из столбца ЗБП последнего оптимального плана симплексной таблицы. Если какая либо переменная в этом столбце отсутствует, то в оптимальном плане она равна 0.
Значение целевой функции также берется из столбца ЗБП последнего оптимального плана. Оптимальный вектор переменных обозначаем X*, а оптимальное значение целевой функции F max(X*)
При решении задачи планирования товарооборота( задача о распределе6нии ресурсов), основные переменные указывают на количество реализуемой продукции каждого вида, для получения max дохода. А дополнительные переменные указывают на количество недоиспользованных ресурсов каждого вида. Если какая нибудь дополнительная переменная равна 0, то соответствующий ей ресурс использован полностью и является дефицитным. Положительное значение дополнительной переменной говорит о имеющихся излишках ресурсов.
Нулевое значение какой-либо основной переменной говорит о том, что соответствующий товар невыгоден, его реализация нерентабельна.
Вывод о количестве оптимальных решений можно сделать по индексной строке оптимального плана. Если в индексной строке 0 соответствуют только столбцам базисных переменных, то полученное оптимальное решение единственно. Если 0 соответствует небазисной переменной, то задача будет иметь альтернативный оптимум.
Альтернативный оптимум можно найти, если принять за ведущий столбец, столбец с небазисным 0. При этом среди элементов данного столбца должен быть один положительный.
Если известны два оптимальных решения, то в задачи с альтернативным оптим