В хорошо подобранной модели остатки должны

В хорошо подобранной модели остатки должны

- иметь нормальный закон распределения с нулевым математическим ожиданием и постоянной дисперсией,

- не коррелировать друг с другом,

- хаотично разбросаны.

Коэффициент детерминации это

- квадрат множественного коэффициента корреляции.

Квадрат какого коэффициента указывает долю дисперсии одной случайной величины, обусловленную вариацией другой

- коэффициент детерминации,

- парный коэффициент корреляции,

- частный коэффициент корреляции,

- множественный коэффициент корреляции.

5.Величина, рассчитанная по формуле 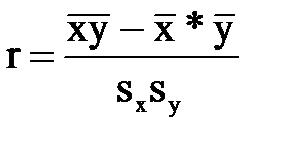является оценкой

- парного коэффициента корреляции,

Отметьте основные виды ошибок спецификации

- отбрасывание значимой переменной,

- добавление незначимой переменной,

- ?выбор неправильной формы модели.

7.На практике о наличии мультиколлинеарности обычно судят по матрице парных коэффициентов корреляции. Если один из элементов матрицы R больше…., то считают, что имеет место мультиколлинеарность и в уравнение регрессии следует включить только один из показателей x_jили x_e. Вставьте недостающее значение.

- 0,8;

8.Оценить значимость парного линейного коэффициента корреляции можно при помощи:

- критерия Стьюдента;

-

9.Степень влияния неучтенных факторов в рассматриваемой модели можно определить на основе:

- коэффициента детерминации;

10.Частный критерий Фишера вычисляется по формуле:

- .

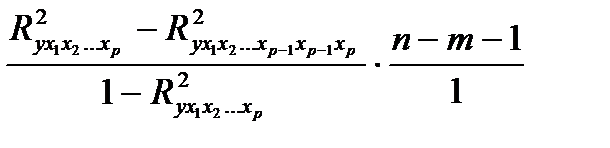11.Уравнение множественной регрессии в стандартизованном виде имеет вид: 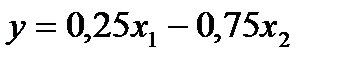. Сила влияния какого фактора выше на результативный признак?

- Сила влияния фактора х₂ на результативный признак выше силы влияния фактора х₁;

12.Наличие гетероскедастичности можно определить используя:

- критерий Энгеля-Грангера.

13.Оценить значимость коэффициентов регрессии в множественной линейной модели можно при помощи:

- критерия Стьюдента;

14.Степень усредненного влияния неучтенных факторов в рассматриваемой модели можно определить на основе:

- коэффициента регрессии.

Коэффициент множественной детерминации показывает

- долю вариации зависимой переменной, обусловленную вариацией независимых переменных;

16.О модели регрессии 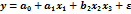можно сказать, что это регрессия

- второго порядка
- линейная
- нелинейная
- простая   17.С помощью значений таблицы дисперсионного анализа определить значимость регрессии, используя F-критерий. Критическое значение F(α,f1,f2) = 4.3 при уровне значимости α=0.05 и степенях свободы f1= 1 и f2= 25. Какой вывод можно сделать о качестве использованной модели регрессии?

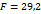- –Модель адекватна исходным данным

Гетероскедастичность регрессионной модели – это

- непостоянство дисперсий ошибок регрессии для различных значений объясняющей переменной

Какой из приведенных тестов является тестом на гетероскедастичность?

- Голдфелда-Квандта

-

Парабола третьего порядка

Многофакторная

4. линейная.
Укажите соответствие для каждого нумерованного элемента задания
* y = a + b⋅x + c⋅x² + d⋅x³ + ε -2 2
* y = a + b⋅x₁ + c⋅x₂ + d⋅x₃ + ε -3 3
* y = a + b⋅x + ε – 4 4
*1/ y = a + bx + ε – 1 1

В хорошо подобранной модели остатки должны

- иметь нормальный закон распределения с нулевым математическим ожиданием и постоянной дисперсией,

- не коррелировать друг с другом,

- хаотично разбросаны.