Метод математической индукции

Во многих разделах математики приходится доказывать истинность утверждения, зависящего от 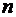, т.е. истинность высказывания p(n) для "nÎN (для любого nÎN p(n) верно).

Часто это удается доказать методом математической индукции.

В основе этого метода лежит принцип математической индукции. Обычно он выбирается в качестве одной из аксиом арифметики и, следовательно, принимается без доказательства. Согласно принципу математической индукции предложение p(n) считается истинным для всех натуральных значений переменной, если выполнены два условия:

1. Предложение p(n) истинно для n = 1.

2. Из предложения, что p(n) истинно для n = k (k - произвольное натуральное число) следует, что оно истинно для n = k + 1.

Под методом математической индукции понимают следующий способ доказательства

1. Проверяют истинность утверждения для n = 1 – база индукции.

2. Предполагают, что утверждение верно для n = k – индуктивное предположение.

3. Доказывают, что тогда оно верно и для n = k + 1 индуктивный переход.

Иногда предложение p(n) оказывается верным не для всех натуральных n, а начиная с некоторого для n = n₀. В этом случае в базе индукции проверяется истинность p(n) при n = n₀.

Пример 1. Пусть 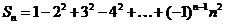. Доказать, что

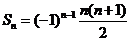
1. База индукции: при n = 1 по определению S₁ = 1 и по формуле 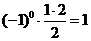получаем один результат. Утверждение верно.

2. Индуктивное предположение. Пусть n = k и .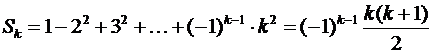

3. Индуктивный переход. Пусть n = k + 1. Докажем, что .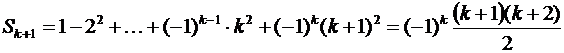

Действительно, в силу индуктивного предположения

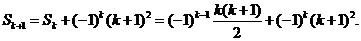
Преобразуем это выражение

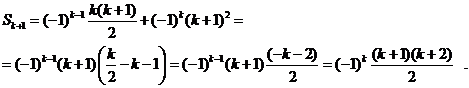
Индуктивный переход доказан.

Замечание.Полезно записать, что дано (индуктивное предположение) и что нужно доказать!

Пример 2. Доказать

.

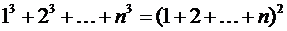1. База индукции. При n = 1, утверждение, очевидно, верно.

2. Индуктивное предположение. Пусть n = k и

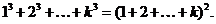
3. Индуктивный переход. Пусть n = k + 1. Докажем:

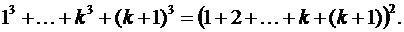
Действительно, возведем правую сторону в квадрат как сумму двух чисел:

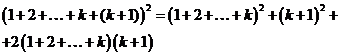
Используя индуктивное предположение и формулу суммы арифметической прогрессии: 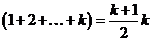, получим

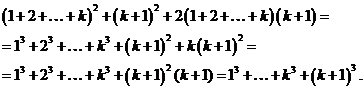
Пример 3.Доказать неравенство

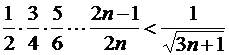для .

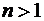1. Базой индукции в этом случае является проверка истинности утверждения для 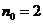, т.е. необходимо проверить неравенство 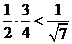. Для этого достаточно возвести неравенство в квадрат: 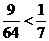или 63 < 64 – неравенство верно.

2. Пусть неравенство верно для 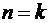, т.е.

.

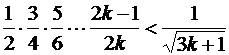3. Пусть 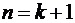, докажем:

.

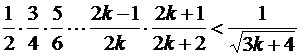Используем предположение индукции

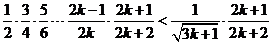
Зная как должна выглядеть правая сторона в доказываемом неравенстве выделим эту часть

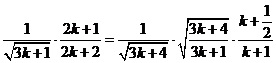
Остается установить, что лишний множитель 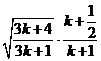не превосходит единицы. Действительно,

.

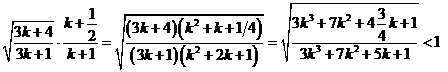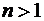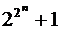Пример 4. Доказать, что при любом натуральном число оканчивается цифрой .

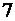1. Наименьшее натуральное 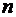, с которого справедливо утверждение, равно . .

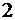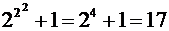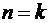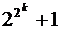2. Пусть при число оканчивается на 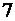. Это означает, что это число можно записать в ви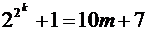де , где 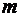– какое-то натуральное число. Тогда .

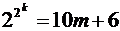3. Пусть 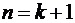. Докажем, что 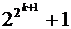оканчивается на 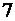. Используя полученное представление, получим

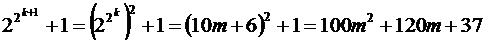
Последнее число имеет ровно 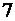единиц.

Задачи.

1. Доказать, что при каждом 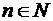верны равенства

1) .

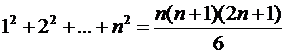2) .

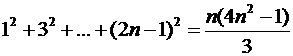3) .

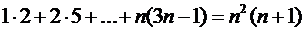4) .

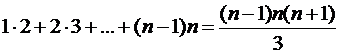5) .

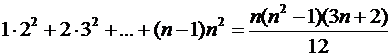6) .

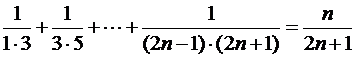7) .

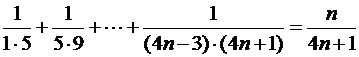8) .

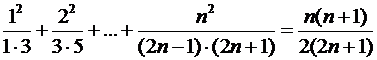9) .

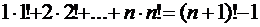10) .

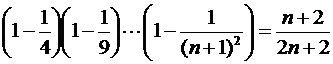2. Доказать, что при любом .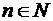

1) 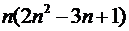кратно .

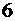2) 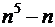кратно .

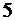3) 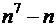кратно .

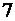4) 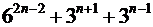кратно .

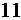5) 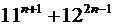кратно .

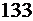6) 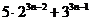кратно 19.

3. Доказать справедливость следующих неравенств для всех натуральных .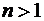

1) .

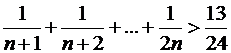2) .

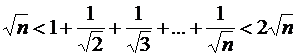3) .

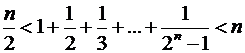4) .

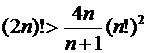5) .

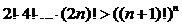4. Доказать, что при любом натуральном 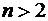верно неравенство

1) 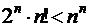. 2) .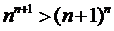

5. Доказать равенство для любого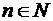

1) ,

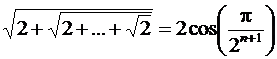(в левой части содержится 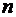корней).

2) .

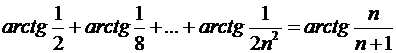6. Пусть 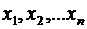– произвольные неотрицательные числа, причем

.

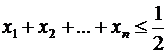Доказать, что .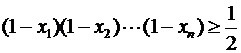

7. Доказать неравенство Бернулли

,

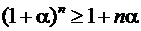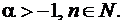
8.Пусть 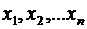– произвольные положительные числа, причем

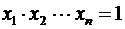. Доказать, что .

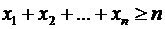Приложение

«Нельзя повредить истине более, чем желанием построить ее на ложных умозаключениях» П.Монертюи

Аксиомы теории множеств

Ниже мы приводим перечень аксиом теории множеств, которые использовались различными математиками для построения аксиоматической теории множеств. Этот перечень не является полным, в него включены аксиомы, посвященные основам теории множеств. Существует ряд аксиом, связанных с более глубокими понятиями в теории множеств. Перечисленные ниже аксиомы нельзя рассматривать и как единый набор, так как в совокупности они являются зависимыми.

1. Аксиома объемности. Если множества А и В составлены из одних и тех же элементов, то они совпадают.

2. Аксиома существования пустого множества. Существует такое множество Æ, что ни один элемент х ему не принадлежит.

3.Аксиома пары. Для произвольных а и b существует множество, единственными элементами которого являются а и b.

4. Аксиома суммы.Для каждого семейства множеств А существует множество S, состоящее из тех и только тех элементов, которые принадлежат некоторому множеству Х, принадлежащему А.

5. Аксиома степени. Для каждого множества А существует семейство множеств Р, элементами которого являются все подмножества множества А и только они.

6. Аксиома бесконечности. Существует такое семейство множеств А, которому принадлежит Æ и если, ХÎА, то в А найдется элемент Y, состоящий из всех элементов множества Х и самого множества Х.

7. Аксиома выбора. Для каждого семейства А непустых непересекающихся множеств существует множество В, имеющее один и только один общий элемент с каждым из множеств Х, принадлежащих А.

8. Аксиома выделения для высказывательной функции Ф. Для произвольного множества А существует множество, состоящее из тех и только тех элементов множества А, которые (будучи подставлены на место переменных х) удовлетворяют Ф.

9. Аксиома замены для высказывательной функции Ф. Если для каждого х существует единственный элемент у, такой что выполняется Ф(х, у), то для каждого множества А существует множество В, состоящее из тех и только тех элементов у, которые при некотором хÎА выполняют Ф(х,у).

10. Аксиома регулярности. Для любого непустого семейства множеств А существует такое множество Х, что ХÎА и ХÇА = Æ.

В систему аксиом Цермело (первую предложенную систему аксиом) входили аксиомы 1, 5, 6, 7, 8. В системе Цермело-Френкеля аксиома 8 была заменена на аксиому 9. В настоящее время системы аксиом различаются по типам: наиболее известными считаются системы Цермело-Френкеля и Геделя-Бернайса. Обычно в систему аксиом Цермело-Френкеля включают аксиомы 1-6, 9.

Биографическая справка

БОЛЬЦАНО, БЕРНАРД (5.10.1781-18.12.1848) - чешский математик, философ и логик. При жизни Б. напечатал только пять небольших математических сочинений и ряд философских трудов, вышедших анонимно. Большой математический труд Б. "Учение о функциях", написанный в 1830, увидел свет только через 100 лет. В нем, в частности, Б. (за 30 лет до К. Вейерштрасса) строит пример непрерывной кривой, не имеющей касательной ни в одной точке. Б. установил современное понятие сходимости рядов и за несколько лет до выхода в свет "Алгебраического анализа" О .Л. Коши пользовался критерием сходимости, именуемым обычно критерием Коши. Теорему, устанавливающую, что всякое бесконечное множество чисел, заключенных в замкнутом интервале, имеет в нем по меньшей мере одну предельную точку, Б. упоминает за много лет до того, как ее сформулировал К. Т. В. Вейерштрасс. Уточнив понятия предела и непрерывности, Б. впервые строго доказал теорему о том, что непрерывная функция принимает любое промежуточное значение, лежащее между двумя ее разными значениями. В "Парадоксах бесконечного" (издано в 1851), написанных Б. в последний год жизни, содержится определение бесконечного множества как равномощного своей правильной части, здесь Б. явился предшественником Г. Кантора - творца теории множеств. В начале 30-х годов 19 в. Б. сделал попытку построения теорий действительных чисел, которая после некоторых уточнений совпадает с теорией Г. Кантора. В классическом анализе и теории функций известен принцип выбора Больцано, лемма Больцано-Вейерштрасса об ограниченной последовательности и др.

ВИНЕР, НОРБЕРТ(Wiener, Norbert) (1894–1964), американский математик. Мальчик был вундеркиндом: в возрасте трех лет он начал читать и писать, семи лет читал Дарвина и Данте, в одиннадцать окончил среднюю школу, в четырнадцать – Тафтс-колледж. Учился в Гарвардском университете, в 17 лет стал магистром искусств, в 18 – доктором философии по специальности «математическая логика». Первую математическую работу Винер опубликовал в 19 лет. В 1932 получил звание профессора МТИ. В 1945–1947 Винер заинтересовался системами с обратной связью и проблемами передачи, хранения и переработки информации. Новую науку – общую теорию управления и связи – он назвал кибернетикой. В 1948 вышла книга Винера Кибернетика, живо воспринятая мировым научным сообществом. Под влиянием высказанных в ней идей возникло немало научных направлений и появилась масса научных работ.

ГЕДЕЛЬ, КУРТ(Родился 28 апреля 1906 в Брно. Умер в Принстоне 14 января 1978.) Австрийский математик. В 1924 году поступил в Венский университет, в 1930 защитил докторскую диссертацию по математике. В 1933–1938 – приват-доцент Венского университета; в 1940 эмигрировал в США. С 1953 и до конца жизни – профессор Принстонского института перспективных исследований. Диссертация Гёделя была посвящена проблеме полноты.

В 1930-е годы были получены некоторые результаты о полноте различных аксиоматических систем. Так, Гильберт построил искусственную систему, охватывающую часть арифметики, доказал ее полноту и непротиворечивость. Гёдель в своей диссертации доказал полноту исчисления предикатов первой ступени, и это дало надежду математикам на то, что им удастся доказать непротиворечивость и полноту всей математики. Однако уже в 1931 тот же Гёдель доказал теорему о неполноте, нанесшую сокрушительный удар по этим надеждам. В то время Давид Гильберт и другие великие ученые пытались свести всю математику к системе аксиом. Но Гедель доказал, что это не совсем реально. Работа Геделя произвела эффект разорвавшейся бомбы. Она заставила фон Неймана прервать курс лекций в Геттингене, а Гильберта - прекратить работу над своей программой.

Согласно теореме Геделя о неполноте, любая процедура доказательства истинных утверждений элементарной теории чисел обречена на неполноту. Следовательно, внутренняя непротиворечивость любой математической теории не может быть доказана иначе, как с помощью обращения к другой теории, использующей более сильные допущения, а значит, менее надежной.

Методы, использованные Гёделем при доказательстве теоремы о неполноте, сыграли в дальнейшем важную роль в теории вычислительных машин.

Гёдель внес важный вклад в теорию множеств. Два принципа – аксиома выбора и континуум-гипотеза – на протяжении десятилетий не поддавались доказательству, но интерес к ним не ослабевал: слишком привлекательны были их логические следствия. Гёдель доказал (1938), что присоединение этих принципов к обычным аксиомам теории множеств не приводит к противоречию.

ДЕДЕКИНД, РИХАРД ЮЛИУС ВИЛЬГЕЛЬМ (Dedekind Richard) (6.10.1831-12.2.1916) - немецкий математик, член Берлинской Академии Наук (1880г.). Работал в Цюрихском университете, с 1862г. - профессор Высшей технической школы в Браупшвейге. Основные труды по теории алгебраических чисел. Изложил их в "Одиннадцатом дополнении" к "Лекциям по теории чисел" Дирихле. В трудах Дедекинда заложены основы современной алгебры, изучающей произвольные поля, кольца, группы, структуры и модули. В частности, ввел понятие кольца и (независимо от Е. И. Золотарева) дал современное общее определение идеала. В ходе работ по теории идеалов Дедекинд пришел к рассмотрению понятия упорядоченного множества в более общей форме, чем у Г. Кантора. Одним из первых дал теоретико-множественное обоснование теории действительных чисел. Сформулировал (1888г.) систему аксиом арифметики (ее обычно называют аксиомами Пеано), содержащую, в частности, точную формулировку принципа полной математической индукции. Ввел в математику в самом общем виде теоретико-множественное понятие отображения. С именем Дедекинда связаны многочисленные математические утверждения и термины: кольцо, поле, структуры, сечения, функции, теоремы, принцип взаимности.

КАНТОР, ГЕОРГ ФЕРДИНАНД ЛЮДВИГ ФИЛИПП (Родился: 3 марта 1845 в Санкт-Петербурге, Россия. Умер: 6 января 1918 в Галле, Германия) Отец Георга Кантора Вальдемар Кантор работал оптовым агентом в Санкт-Петербурге, а позже брокером на Фондовой бирже Санкт-Петербурга. Он родился в Дании и был человеком неравнодушным к культуре и искусству. Мать Георга, Мария Анна Бохм, была русской и увлекалась музыкой. И конечно же, Георг унаследовал немалые музыкальные и художественные дарования от своих родителей, став выдающимся виолончелистом.

После начальных занятий с домашним учителем, Кантор стал посещать школу в Санкт-Петербурге, затем, когда ему исполнилось 11 лет, его семья уехала в Германию. Однако, Кантор: вспоминал свои детские годы в России с большой ностальгией, и никогда не чувствовал себя легко в Германии, хотя прожил там всю оставшуюся жизнь и, по-видимому, никогда не писал на русском языке, который знал.

Сначала они жили в Вьезбадене, где Кантор стал посещать гимназию, а потом они переехали во Франкфурт, где он стал учиться в Realschule в Дармштадте и жить на пансионе. Realschule он закончил в 1860 с отличием, в котором было указано на особые способности в математике, особенно в геометрии. В 1862 году он поступил в политехнический институт в Цурихе. Отец хотел, чтобы Кантор стал ... светилом технического "мира". Но Кантору удалось получить отцовское разрешение на изучение математики в Университете. Его обучение в Цурихе, однако, прекратилось из-за смерти отца в июне 1863 года. Кантор перевелся в Университет в Берлине, где он подружился с Германом Шварцом, который учился с ним в одной группе. Кантор посещал лекции Вейерштрасса , Каммера, и Кронеккера. В 1867 году он завершает свою диссертацию по теории чисел De aequationibus secondi gradus indeterminatis.

После переезда в Холл направление исследований Кантора сменилось от теории чисел к анализу. Это случилось благодаря Гейну, который предложил Кантору доказать единственность представления функции в виде тригонометрического ряда. Это была трудная задача, которую пытались решить многие математики, такие как Дирихле, Липшиц, Риман, и безуспешно. Кантор решил эту задачу, доказав единственность представления в апреле 1870.

В 1873 году Кантор доказал счетность множества рациональных чисел. В декабре 1873 года он доказал, что действительные числа не являются счетными и опубликовал это в своем труде в 1874 году.

Следующий вопрос, который его заинтересовал, это можно ли установить взаимно однозначное соответствие между единичным квадратом и отрезком единичной длины. В письме Дедекинду от 5 января 1874 года он писал: - Может ли поверхность (скажем, квадрат вместе со своей границей) быть единственным образом преобразованным в линию (скажем, прямолинейный сегмент вместе с конечными точками (отрезок)) да так, что у каждой точки квадрата будет свой образ на отрезке и наоборот? Я думаю, что ответ на этот вопрос будет не так легко найти, несмотря на тот факт, что ответ кажется понятным "НЕТ", и доказательство кажется почти ненужным.

1874 год был очень важным для личной жизни Кантора. Он был помолвлен с Валли Гуттманн, подругой его сестры. Они поженились 9 августа 1874 года и провели свой медовый месяц в Интерлейкен в Швейцарии, где Кантор провел много времени в математических дискуссиях с Дедекиндом.

Кантор продолжил переписку с Дедекиндом. В 1877 в письме к Дедекинду он приводит доказательство, что существует взаимно однозначное соответствие точек числового интервала (0,1) и точек р-мерного пространства. Кантор был удивлен собственному открытию и написал :

- Я вижу, но я не верю!

Конечно, этот факт имел свои следствия в геометрии и теории размерности пространств. Основной труд о размерности, который Кантор представил на рассмотрение в Crelle's журнал в 1877 году был подвергнут сомнениям Кронеккером, и был опубликован после вмешательства Дедекинда. Кантор очень обиделся на противостояние Кронеккера и никогда больше не предоставлял на рассмотрение дальнейшие труды в этот журнал.

Труд о размерности, который появился в Crelle's журнале в 1878 году сделал концепцию взаимно однозначного соответствия общепринятой. Между 1879 и 1884 годами Кантор опубликовал серию из 6 трудов в Mathematische Annalen с целью представить основной вводный курс в теорию множеств. Пятый труд из этой серии Grundlagen einer allgemeinen Mannigfaltigkeitslehre был также опубликован как отдельная монография, что было очень важным по нескольким причинам. В первую очередь, Кантор осознал, что развитая им теория множеств не получала широкого признания среди математиков, на которое он надеялся.

В конце мая 1884 года у Кантора был первый приступ депрессии. Казалось, что этот упадок был из-за его творческих переживаний. В этот период Кантор размышлял над доказательством континуум-гипотезы о том, что порядок бесконечного множества действительных чисел следующий за порядком натуральных чисел. Его беспокоило, что он не может ни доказать, ни опровергнуть эту гипотезу. Одно время он думал, что доказал ложность данного утверждения, но затем понял, что ошибался. Затем ему казалось, что он установил истинность данного утверждения, но вновь находил ошибку в своих рассуждениях.

Кантор был избран президентом Deutsche Mathematiker-Vereinigung на первом собрании в 1891 году и продержался на этом посту до 1893 года.

Его последние труды по теории множеств появились 1895 и 1897 годах, снова в Mathematische Annalen и были прекрасными исследованиями трансфинитивной арифметики.

В 1897 Кантор посетил первый Международный Конгресс Математиков в Цюрихе. На Конгрессе Кантор встретил Дедекинда и они возобновили дружбу. Ко времени Конгресса Кантор обнаружил первый из парадоксов в теории множеств и написал Гильберту в 1896, объясняя парадокс ему. На конгрессе работы Кантора были поддержаны многими выдающимися математиками того времени. Гурвиц открыто выражал большое восхищение Кантором и объявил его одним из тех, благодаря кому теория функций была существенно обогащена. Жак Адамар выразил мнение, что понятия теории множеств являются важным аппаратом, необходимым для дальнейшего развития математики. Именно на этом конгрессе Давид Гильберт произнес свою знаменитую фразу: “Никто не сможет изгнать нас из рая, созданного Кантором”.

Кантор удалился от дел в 1913 и провел свои последние годы больным. Он умер от сердечного приступа.

Гильберт описал работы Кантора как:-

...Самое прекрасное произведение математического гения и одного из высших достижений вполне интеллектуальной человеческой деятельности.

ПУАССОН, СИМЕОН ДЕНИ(Poisson, Simeon-Denis) (1781–1840), французский математик, механик и физик. В 17 лет Пуассон поступил в Политехническую школу в Париже, в 1809 он стал профессором Парижского университета. Пуассона интересовали применения математики к механике и физике, которые привели его к открытиям в чистой математике. В 1811 он вывел получившее широкое применение уравнение, связывающее электрический потенциал с плотностью пространственного распределения заряда (уравнение Пуассона). Занимаясь теорией азартных игр, ввел одно из важнейших распределений вероятностей случайных величин (распределение Пуассона) и доказал теорему Пуассона, являющуюся частным случаем закона больших чисел. О том, насколько плодотворной и многосторонней была его деятельность, можно судить по таким терминам, как «скобки Пуассона» (теория дифференциальных уравнений), «коэффициент Пуассона» (теория упругости), «интеграл Пуассона» (интегральное исчисление) и т.д., фигурирующих в учебниках по математике, механике, физике.

Литература

1. Александров П.С. Введение в теорию множеств и общую топологию. М.: Наука, 1977.- 368 с.

2. Бурбаки Н. Теория множеств. М.: Мир, 1965.- 455 с.

3. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. М.: Наука, 1972.- 496 с.

4. Куратовский К. Топология. Ч. 1. М.: Мир, 1966.- 594 с.

5. Куратовский К., Мостовский А. Теория множеств. М.: Мир, 1970.- 416 с.

6. Макаров Б.М., Голузина М.Г., Лодкин А.А., Подкорытов А.Н. Избранные задачи по вещественному анализу. М.: Наука, 1992.- 432 с.

7. Очан Ю.С. Сборник задач и теорем по теории функций действительной переменного. М.: Просвещение, 1965.- 231 с.

8. Столл Р.Р. Множества. Логика. Аксиоматические теории. М.: Просвещение, 1968.- 232 с.

9. Теляковский С.А. Сборник задач по теории функций действительного переменного. М.: Наука, 1980.- 111 с.

10. Виленкин Н.Я. Рассказы о множествах. М.: Наука. 1965.

11. Лавров И.А., Максимова Л.Л. Задачи по теории множеств, математической логике и теории алгоритмов. М.: Физматлит. 2004. – 256 с.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ

R - множество действительных чисел, 4

Q - множество рациональных чисел, 4

N - множество натуральных чисел, 4

Z - множество целых чисел, 4

Æ - пустое множество, 4

È _aÎI А_a, 6

Î - символ принадлежности., 3

[x], 11

b(А), 10

card(A)., 16

D_S, 10

F ^-1, 15

R₂, 10

R_S, 10

S^-1, 11

xSy, 10

А включено в множество В, 5

АÍВ, 5; 6; 10

А-В, 5

ВÊА, 5

В^C, 6

аксиома бесконечности, 27

аксиома выбора, 27

аксиома выбора Геделя,, 4

аксиома выделения для высказательной функции Ф, 27

аксиома замены для высказательной функции Ф, 27

аксиома объемности, 26

аксиома пары, 26

аксиома регулярности, 27

аксиома степени, 27

аксиома суммы., 26

аксиома существования пустого множества, 26

антисимметрия, 24

аргумент, 14

биекция, 14

бинарное отношение, 10

булеан, 10

всюду определенная функция, 14

диагональный метод Кантора., 20

диаграмма Венна, 6

дополнительное множество, 6

законы де Моргана:, 7

интуитивный принцип абстракции Г.Кантора, 4

интуитивный принцип объемности Г. Кантора (1 аксиома Геделя), 3

инъекция, 14

иррефлексивность, 25

класс эквивалентности, 11

класс эквивалентности порожденный х, 11

континуум, 20

левая грань множества, 25

левое обратное отношение, 14

мощность множества А меньше мощности множества В, 16

не более чем счетное множество., 18

обратное отношение, 11

область значений функции, 13

область определения функции, 13

образ, 14

обратная функция, 15

объединение множеств., 5

однозначное отображение, 14

отношение на, 11

отношение, 10

отношение эквивалентности, 11

отображение на, 14

пересечение множеств., 6

парадокс Б.Рассела, 4

правая грань множества, 25

правое обратное отношение, 14

правый экстремальный (левый) элемент, 26

предпорядк, 25

принцип двойственности, 7

произведение множеств, 10

равномощность множеств, 16

разбиение множества, 11

разность множеств, 5

рефлексивность, 11

симметрическая разность множеств., 6

симметричность, 11

строгий порядок, 25

суперпозиция функций, 14

счетное множество, 18

сюръекция, 14

теорема Кантора-Бернштейна., 20

точная левая грань множества, 25

точная правая грань множества, 26

транзитивность, 11

универсум, 7

функция, 13

частичный порядок, 25

Содержание

Введение
1 Понятие множества
2 Включение множеств. Операции над множествами
3 Произведение множеств. Бинарные отношения. Отношение эквивалентности
4 Функция
5 Мощность множеств. Конечные множества
6 Теоремы о счетных множествах. Множества мощности континуум
7 Сравнение мощностей
8 Примеры равномощных множеств
9 Отношение порядка
10 Элементы комбинаторики
Список литературы
Приложение А. Аксиомы теории множеств
Приложение Б. Предметный указатель

[1] См. биографическую справку