Произведение множеств. Бинарные отношения. Отношение эквивалентности.

Определение. Пусть А и В - множества. Произведением множеств А и Вназывается множество всех упорядоченных пар (а, в), где аÎА и вÎВ. Произведение обозначается А´В.

А´В={(a,b):aÎA и bÎB}.

Произведение двух множеств часто называют прямым или декартовым произведением. Заметим, что произведение n штук одного и того же множества А обозначается через Аⁿ .

Примеры. 1) Если А = {a, b}, B = {0, 1}, C = Æ, то

А´В = {(a, 0), (a, 1), (b, 0), b, 1)},

B´A = {(0, a) (0, b), (1, a), (1, b)},

A´C = C´A = Æ.

2) Пусть R – множество действительных чисел. Тогда R² – множество, которое обычно изображается в виде плоскости, а элементы из R² называются точками плоскости.

3) Пусть [a, b], [c, d] – отрезки прямой. Тогда [a, b]´[c, d] – прямоугольник на плоскости.

Определение. Бинарным отношением(или просто отношением) в А´В называется любое подмножество множества А´В.

Примеры. 1) Пусть А = {1, 2, 3}, B = {1, 2, 3, 4, 5, 6, 7}. Тогда A´B = {(1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (1,7), (2,1), (2,2), (2,3), (2,4), (2,5), (2,6), (2,7), (3,1), (3,2), (3,3), (3,4), (3,5), (3,6), (3,7)}.

2) Возьмем S = {(1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (1,7), (2,2), (2,4), (2,6), (3,3), (3,6)}. Ясно, что SÍA´B, т.е. S является бинарным отношением в A´B. Это отношение может быть охарактеризовано следующей формой

S = {(x,y)ÎA´B: xÎA является делителем yÎB}.

3) Пусть А некоторое множество, а b(А) множество всех его подмножеств. Множество b(А) называется булеаном. Пусть W отношение в b(А) ´ b(А), задаваемое формой:

W = {(B, C)Îb(A)´b(A): BÍC}.

Тогда W является отношением включения множеств.

Если S является некоторым отношением и (x, y)ÎS, то мы будем писать xSyи говорить, что x находится в отношении S с y.

Если S является отношением в А´А, то говорят, что S является отношением в А.

Пусть S некоторое отношение в А´В. Введем два множества:

D_S= {aÎA: $bÎB: (a,b)ÎS},

R_S= {bÎB: $aÎA: (a,b)ÎS}.

Множество D_S называется областью определения отношения, а множество R_S – областью значений. Если D_S = A, то такое отношение называют всюду определенным, а если R_S = B – сюръективным. Когда отношение одновременно является сюръективным и всюду определенным, то говорят, что S отношение наА´В (соответственно на А, если В=А).

Отношение S называется инъективным, если из (a, b)ÎS и (c, b)ÎS следует, что а = с. Если отношение S является всюду определенным, инъективным и сюрьективным, то его называют биективным .

Иногда отношения называются соответствием между элементами множества А и В.

Пусть S некоторое отношение в А´В. Введем отношение S^-1следующим образом: (у, х) ÎS^-1 Û (х, у) ÎS. Отношение S^-1 назовем обратным отношением.

Определение. Отношение S на множестве А называется отношением эквивалентности, если оно удовлетворяет следующим условиям:

1) аSа для "аÎА (рефлексивность);

2) если аSв, то вSа (симметричность);

3) если аSв и вSс, то аSс (транзитивность).

В дальнейшем отношение эквивалентности будем обозначать значком ».

Определение. Пусть задано отношение эквивалентности на А. Множество ХÍА называется классом эквивалентностидля этого отношения, если оно удовлетворяет следующим условиям:

1) для любых хÎХ и уÎХ выполняется х » у;

2) если хÎХ , уÎА и х » у, то уÎХ.

Пусть на А задано отношение эквивалентности. Введем следующее обозначение:

[x]= {yÎA: x » y}.

Нетрудно видеть из определений, что [x] является классом эквивалентности. Его называют классом эквивалентности, порожденным элементом х.

Лемма 1. Для классов эквивалентности [x] и [y] возможны только следующие два случая:

1) [x] = [y];

2) [x]Ç[y] = Æ.

Доказательство. Предположим, что [x]Ç[y]¹Æ и аÎ[x]Ç[y]. Тогда x » a и y » a. Покажем, что в этом случае один класс эквивалентности содержится в другом, а так как они равнозначны, то будет доказано равенство этих классов.

Пусть вÎ[x]. Тогда х » в, а » х, следовательно в » а. Но а » y, значит в » y и вÎ[y], т.е. [x]Í[y].

Пусть некоторое множество А представимо в виде:

А = È_a А , где А_a ÇА_b = Æ , если a ¹ b.

В этом случае говорят, что {A_a} задает разбиение А. Из доказанной леммы вытекает, что классы эквивалентности задают разбиение на А. Оказывается, верно и обратное.

Лемма 2. Если {A_a} - некоторое разбиение множества А, то отношение S, определяемое следующим условием: аSв Û $ a: аÎА_a и вÎА_a, является отношением эквивалентности.

Доказательство. По существу, в доказательстве нуждается лишь третье свойство эквивалентности. Пусть аSв и вSс. Тогда из задания отношения S вытекает следующее: $ a: аÎА_a и вÎА_a , а также $ b: вÎА_b и сÎА_b . Тогда вÎА_a Ç А_b и из свойств разбиения следует, что А_a = А_b или a = b, следовательно, аÎА_a и сÎА_a . Это доказывает, что аSс и отношение S является отношением эквивалентности.

Теорема. Пусть S - некоторое отношение эквивалентности на А. Пусть {А_a} - разбиение множества А, порожденное этим отношением (лемма 1). Пусть Т - отношение эквивалентности, порожденное разбиением {А_a} (лемма 2). Тогда S=T.

Доказательство. Для доказательства напомним, что S и T являются подмножеством А´А и их равенство понимается как равенство множеств. Пусть (а,в)ÎS, т.е. аSв. Тогда а и в из одного класса эквивалентности, т.е. $ a: аÎА_a и вÎА_a. Это означает, что (а,в)ÎT и SÍT. Аналогично показывается обратное включение.

Задачи.

1. Доказать, что существуют А, В и С такие, что

а) А´В ¹ В´А;

б) А´(В´С) ¹ (А´В) ´С.

2. Доказать, что если А, В, С и D не пусты, то

а) АÍВ и СÍD Û А´СÍВ´D;

б) А=В и С=D Û A´C = B´D.

3. Доказать, что

а)(АÇВ)´(СÇD) = (А´С)Ç(В´D);

б)(А´В)È(C´D) Í(AÈC)´(BÈD);

в)(АÈВ)´С=(А´С)È(В´С);

г)А´(ВÈС)=(А´В)È(А´С);

д)(АÈВ)´(CÈD)=(A´C)È(B´C)È(A´D)È(B´D);

е)(А-В)´С=(А´С)-(В´С);

ж)А´(В-С)=(А´В)-(А´С);-

з)А´В=(A´D)Ç(C´B), где АÍС и BÍD.

4. Найти область определения и область значений для отношений:

а) R={(x,y): x, yÎN и x делит y};

б) R={(x,y): x, yÎN и y делит x};

в) R={(x,y): x, yÎR и x+y ³0};

г) R={(x,y): x,yÎR и 2x>3y}.

5. Пусть R, S, T - некоторые отношения. Проверить справедливость равенств:

а) Ro(SoT) = (RoS)oT;

б) (R^-1)^-1 = R;

в) (RoS)^-1 = S^-1oR^-1.

6. Пусть на множестве А заданы отношения R₁ и R₂. Доказать:

а) если отношения R₁ и R₂ рефлексивны, то рефлексивны отношения R₁ÈR₂, R₁ÇR₂, R₁^-1, R₁oR₂;

б) если отношения R₁ и R₂ иррефлексивны (т.е. для " хÎ А не выполняется хRх), то иррефлексивны R₁È R₂, R₁ÇR₂, R₁^-1, суперпозиция R₁оR₂ может быть иррефлексивной;

в) если отношения R₁ и R₂ симметричны, то симметричны отношения R₁ÈR₂, R₁ÇR₂, R₁^-1, R₁oR₂^-1;

г) отношение R₁oR₂, где R₁ и R₂ симметричны, симметрично тогда и только тогда, когда R₁oR₂ = R₂oR₁;

д) если отношения R₁ и R₂ антисимметричны, то антисимметричны R₁ÇR₂, R₁^-1.

7. Пусть А - конечное множество, n - число его элементов. Доказать, что число подмножеств множества А, состоящих из m элементов, где 0£ m £n, равно

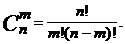
8. Пусть r - отношение, обладающее свойством рефлексивности и транзитивности в множестве А. Определим для а, bÎА отношение R, полагая аRb, если аrb и brа.

а) Доказать, что R есть отношение эквивалентности на А.

в) Доказать, что если аRа', bRb' и аrb, то а'rb'.

9. Во множестве Z⁺´Z⁺ положим по определению (а, b)r(с, d), если а+d=b+с. Доказать, что r является отношением эквивалентности на данном множестве.

«Понятие функции такое же основное, как и понятие множества» Хаусдорф

Функция

Пусть Х и У два множества и F отношение в Х´У.

Определение. Отношение F называется функциейиз Х в У, если оно удовлетворяет свойству:

из xFy и xFz следует, что y = z.

В дальнейшем мы будем применять также обозначение y = F(x) вместо xFy, если F является функцией. Множества D_F и R_F , введенные в предыдущем пункте для функции F носят соответственно названия: D_F - область определенияи R_F - область значенийфункции F. Очень часто область определения и область значений заранее не задаются, а возникают, исходя из задания функции.

Примеры.

1) {(1,2), (2,2), (Рузвельт, Черчилль)};

2) {(1,2), (1,3), (2,2)};

3) {(x, x² +x+1)|xÎR};

4) {(x² ,x)|xÎR}.

Из приведенных примеров 1 и 3 определяют функцию, а 2 и 4 не являются функцией, т.к. не выполнено определение функции.

Для функции применяются также другие названия: преобразование, отображение, соответствие. Если y = F(x), то x называют аргументомфункции, а y образом.

Две функции F и G считаются равными, если выполнены равенства соответствующих множеств. Последнее эквивалентно следующим двум равенствам:

D_F =D_G и F(x)=G(x) для "xÎD_F.

Следующие определения переносятся с отношений:

1) В случае, когда D_F = Х функцию называют всюду определенной.

2) Функция F из Х в У называется сюръекцией(или отображением на), если R_F =У.

3) Функция F из Х в У называется инъекцией(или однозначным отображением), если из х₁ ¹ х₂ следует, что F(х₁) ¹ F(х₂).

Всюду определенная функция F из Х в У называется биекцией, если она одновременно является сюръекцией и инъекцией.

Примеры: 1) функция у=е^x - биекция из R в R₊ ;

2) у=х² - сюръекция из [-1, 1] на [0, 1], не являющаяся инъекцией.

Определение. Пусть F - функция из X в Y, а G - из Y в Z. Суперпозицией функцийF и G называется такая функция H из X в Z, что z = H(x) (т.е. (x, z)Î H Í X´Z) тогда и только тогда, когда y=F(x) и z=G(y). Суперпозиция обозначается GoF. В определении Н – функция, почему?

Определение. Для функции F из Х в У функция G из У в Х называется правой обратной(соответственно, левой обратной), если справедливо равенство FoG=I_У (соответственно, GoF=I_Х), где через I_Х (I_У) обозначено тождественное отображение на Х (соответственно на У), т.е. I_Х(x) = x (I_У(y) = y).

Функция у=х², из рассмотренного выше примера не имеет левой обратной, но имеет правую обратную (ею является функция х= 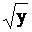). Однако если сузить область определения функции у=х² до отрезка [0,1] (или [-1,0]), оставив туже самую область значений, то эта функция будет иметь уже и левую обратную: х= 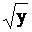(соответственно, х= - ).

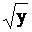Лемма 1. Если функция F имеет левую обратную, то F является инъекцией.

Доказательство. Действительно, если бы F не являлась инъекцией, то существовали бы х₁ ¹ х₂ такие, что y=F(x₁)=F(x₂). Пусть G - левая обратная к F, то x₁ = GoF(x₁ ) = G(y) = GoF(x₂ ) = x₂, что противоречит предположению.

Лемма 2. Если функция F имеет правую обратную, то F является сюръекцией.

Доказательство. Утверждение легко вытекает из определения правой обратной функции G: для любого уÎУ Þ FoG(у)=у.

Лемма 3. Если у функции F из Х в У существуют левая и правая обратная функции, то они совпадают.

Доказательство. Пусть G и H - обозначают соответственно левую и правую обратную функции к F. Тогда D_G = R_F = D_H = У. Остается проверить равенство G(y) = H(y) для любого yÎУ. Но G(y) = G(I_У(y)) = G(F(H(y))) = I_Х(H(y)) = H(y).

Определение. Функция из У в Х, которая является правой и левой обратной к функции F, называется обратной функциейк F и обозначается через F ^-1.

Теорема. Пусть F является функцией из Х в У. Для существования обратной функции F^-1 из У в Х необходимо и достаточно, чтобы F была биекцией.

Необходимость легко вытекает из лемм 1 и 2.

Достаточность. Пусть yÎУ. Так как F является сюръекцией, то существует хÎХ такое, что F(x)=y. При этом такое х одно, так как F также и инъекция. Определим функцию G(x)=y. Легко проверить, что таким образом определенная функция является обратной к F.

Следствие. Если F является биекцией, то и F^-1 также является биекцией.

Задачи.

1. Установить, что следующие отношения являются функцией:

а) вÎУ, R = X´{в}ÍX´У (постоянное отображение);

б) R = {(x, x): xÎX}ÍX´X (тождественное отображение I_X);

в) R = {((x, y), x)}Í(X´Y)´X ( проекция на Х);

г) R = {((x, y), у)}Í(X´Y)´Y ( проекция на Y).

2. Пусть А - произвольное множество из области определения функции f(х). Верно ли равенство f ^-1 [f(A)] = A всегда ?

3. Пусть В - произвольное множество из области значений функции f(х). Верно ли равенство: f[f ^-1 (B)] = B всегда ?

4. Верны ли равенства:

f(AÈB) = f(A)Èf(B);

f(AÇB) = f(A)Çf(B)?

5. Верно ли, что f(R – А) = f(R) – f(А), где R - область определения функции?

6. Пусть А и В - два множества из области значений функции у = f(х). Верны ли равенства:

f ^-1 (AÇB) = f ^-1 (A)Çf ^-1 (B),

f ^-1 (AÈB) = f ^-1 (A)Èf ^-1 (B)?

7. Пусть L - область значений функции у = f(х), а АÍL. Справедливо ли равенство: f ^-1 (L – A) = f ^-1 (L) – f^-1 (А)?

8. Задана функция f: х ® х² + рх + q и интервал (a, b). Определить множество f ^-1 ((a, b)).

9. Задана функция f из А в В. Доказать, что для всякого МÍВ справедливо включение f[f ^-1 (M)] Í M. Пусть Е ÍА. Доказать, что f^-1 [f(E)] ÊE.

10. Задана функция f из А в В. Пусть Е₁ ÍА, Е₂ ÍА, М₁ ÍВ, М₂ ÍВ. Доказать, что если Е₁ ÍЕ₂ , то f(Е₁)Íf(Е₂), если М₁ ÍМ₂, то f ^-1 (М₁) Í f ^-1(М₂).

11. Задана функция f из А в В. Доказать, что следующие условия попарно эквивалентны:

а) f - инъекция;

б) f ^-1 (f(Е)) = Е для любого ЕÍА;

в) f(ЕÇМ) = f(Е)Çf(М) для любых Е, МÍА;

г) f(Е)Çf(М) = Æ для любой пары множеств ЕÍА, МÍА такой, что ЕÇМ= Æ;

д) F(Е – М) = f(Е) – f(М) для любой пары множеств ЕÍА, МÍА такой, что МÍЕ.

12. Пусть даны множества А, В, С, D и функции

f: А ® В, g: В ® С, h: С ® D.

Доказать, что если каждая из суперпозиций gof и hog есть биекция, то и все функции f, g и h являются биекциями.

13. Пусть А - конечное множество и f функция из А в А. Доказать, что

а) если f является сюръекцией, то f также и инъекция;

в) если f является инъекцией, то f также и сюръекция.

14. Построить отношения, удовлетворяющие следующим требованиям:

а) рефлексивное, симметричное, не транзитивное;

б) рефлексивное, транзитивное, не симметричное;

в) симметричное, транзитивное, не рефлексивное.