Множества и операции над ними. отношения и функции. мощность множеств. комбинаторика

МНОЖЕСТВА И ОПЕРАЦИИ НАД НИМИ. ОТНОШЕНИЯ И ФУНКЦИИ. МОЩНОСТЬ МНОЖЕСТВ. КОМБИНАТОРИКА

Учебное пособие

Уфа - 2007

Составители: Ахметова Н.А., Водопьянов В.В.

УДК

Множества и операции над ними. Отношения и функции. Мощность множеств. Комбинаторика. Учебное пособие/Уфимск. авиац. техн. унив-т; Сост. Н.А.Ахметова, В.В.Водопьянов.- Уфа, 2007.- 37 с.

Предлагаемое учебное пособие содержат теоретические и практические задания по разделу, который относится к основаниям математики. Данный раздел читается для студентов, обучающихся на направлениях и специальностях «Прикладная математика и информатика», «Прикладная математика», «Компьютерная математика», как правило, в курсе «Математического анализа». Излагаемый материал представляет интерес и как вводная часть для многих курсов: «Дискретная математика», «Функциональный анализ», «Теория вероятности и математическая статистика» и др. В пособии достаточно подробно рассмотрены вопросы аксиоматического построения теории множеств, операции над множествами, понятие мощности множества. Пособие представляет интерес также для студентов других специальностей, которые изучают упоминаемые разделы математики, в первую очередь для студентов, обучающихся по направлению “Информатика и вычислительная техника”.

Ил. 1. Библиогр.: 9 назв.

Рецензенты:

«Высшее назначение математики…состоит в том, чтобы находить скрытый порядок в хаосе, который нас окружает» Н.Винер[1] «Жизнь украшается двумя вещами: занятием математикой и ее преподаванием» С.Д.Пуассон1

Введение. Понятие множества

С множествами математика, как таковыми, оперирует с начала своего существования. Однако формирование понятия множества начало происходить значительно позже - в 19 веке. Большое влияние на формирование этого понятия оказали работы Больцано¹, Дедекинда¹, Дюбуа-Реймона¹, но эти математики рассматривали лишь конечные множества. Переход к изучению бесконечных множеств и операций над ними представлял принципиальную трудность. Свидетельством последнего являются различные противоречия (антиномии теории множеств), открытые разными учеными к 1900 г. Изучение бесконечных множеств было начато в работах Георга Кантора в 1871-1883 гг., которые встречали активное сопротивление современников. Кантор употреблял вначале термин Inbegrift - “совокупность”, затем Mannigfaltigkeit - “многообразие”, и наконец, Menge - “множество”, в настоящее время сохранилось его обозначение множества M = {m}, которое он ввел в 1895 году. Официальное признание теории множеств прозвучало на Первом международном математическом конгрессе (Цюрих, 1897 г.), где Адамар и Гурвиц указали на важные применения этой теории к анализу. Большое значение в распространении идей теории множеств принадлежит Гильберту. Именно он сказал: “Никто не сможет нас изгнать из рая, созданного Кантором”.

Георг Кантор считается основателем современной теории множеств. В его работах началось построение аксиоматической теории множеств, хотя первая система аксиом теории множеств была предложена позднее в работах Цермело в 1904-1908 гг. Эта система аксиом позволила получить важные для математики результаты по теории множеств. Но лишь в 1940 году Гедель построил наиболее полную систему аксиом и доказал ее непротиворечивость.

Понятие множества с современной точки зрения считается интуитивно заданным. Попытки дать определение множества приводят к сведению понятия множества к другим подобного рода понятиям: совокупность, набор и т.д.

Что же такое множество по Г.Кантору? Множество по Кантору - это любое собрание определенных и различных между собой объектов нашей интуиции или интеллекта, мыслимое как единое целое.

Таким образом, каждое множество состоит из объектов, которые в дальнейшем называются элементами множества. Множества обычно обозначаются большими буквами: А, Х и т.д. Элементы же множеств, как правило, обозначают маленькими буквами: а, х и т.д. Для записи того, что а является элементом множества А применяется значок Î (символ принадлежности).Пишут: аÎА и говорят, что элемент а принадлежит множеству А. В случае, когда а не является элементом множества А, пишут аÏА. Множество может содержать как конечное, так и бесконечное число элементов, соответственно, говорят, что множество конечно или бесконечно.

Интуитивный принцип объемности Г. Кантора (1 аксиома Геделя): множества А и В считаются равными (А = В), если они состоят из одних и тех же элементов.

Рассмотрим некоторые примеры множеств (одновременно мы увидим

некоторые способы их задания):

А = {множество всех положительных четных целых чисел},

В = {множество всех положительных целых чисел, представимых в виде суммы двух положительных нечетных целых чисел},

C = {2, 4, 6},

D = {2, 6, 4}.

Из принципа объемности следует, что справедливы равенства А = В и С = D. Здесь приведены два наиболее принятых способа задания множеств: описательный, когда элементы множества должны удовлетворять определенному свойству или закону, и перечислительный, когда перечисляются все элементы множества. И в том и другом случае множества заключены в фигурные скобки.

Рассмотрим еще два примера: А = {1, 2}, B = {{1}, 2}. Нетрудно заметить, что А ¹ В. Это связано с тем, что множество А состоит из двух элементов: 1 и 2, а множество В из двух элементов: {1} и 2, где {1} не является числом, а является множеством, состоящим из одного элемента.

Для некоторых множеств существуют стандартные обозначения:

Æ - пустое множество, т.е. множество не имеющее ни одного элемента (наличие такого множества предполагается второй аксиомой Геделя);

N- множество натуральных чисел;

Z - множество целых чисел;

Q - множество всех рациональных чисел;

R - множество всех действительных чисел;

Добавление к упомянутым множествам знака “+” выделяет из них только положительные числа, например, Z₊ - множество целых положительных чисел.

Одним из основных приемов задания множества является задание его с помощью так называемых форм, т.е. выражения вида А= {x: P(x)}. Здесь P(x) некоторое высказывание и множество А состоит только из тех x, для которых высказывание P(x) является верным. Например,

A = {x: x² + x + 1 > x};

B = {x: х любит Джона}.

Отметим, что множеству А принадлежат все действительные числа, т.е. оно совпадает с множеством R.

Интуитивный принцип абстракции Г.Кантора: любая форма Р(х) определяет некоторое множество А посредством условия, согласно которому элементами множества А являются в точности такие объекты а, что Р(а) есть истинное высказывание.

Оказалось, что интуитивный принцип абстракции не совсем точен и может привести к парадоксам. Один из таких парадоксов был приведен в 1902 году Б.Расселом. Он состоит в следующем: будем говорить, что множество А обладает свойством D, если для него верно АÏА. Введем теперь множество

Т = {А: А удовлетворяет свойству D}.

Заметим, что если ТÎТ, то множество Т не удовлетворяет свойству D и, следовательно, ТÏТ. Если же ТÏТ, то множество Т удовлетворяет свойству D и, следовательно, ТÎТ.

Приведем пример еще одного парадокса. Это довольно известная история, и у нее есть много версий.

В одном полку жил-был полковой парикмахер, которого по историческим причинам называют брадобреем. Однажды командир приказал ему брить тех и только тех, кто не бреется сам. Брадобрей, получив приказ, сначала обрадовался, потому что многие солдаты умели бриться сами, побрил тех, кто бриться сам не умел, а потом сел на пенек и задумался: а что ему с собой-то делать? Ведь если он будет брить себя, то нарушит приказ командира не брить тех, кто бреется сам. Брадобрей уже решил было, что брить себя не будет. Но тут его осенила мысль, что если он сам себя брить не будет, то окажется, что он сам не бреется, и по приказу командира он должен все-таки себя побрить...

Уточнением интуитивного принципа абстракции является аксиома выбора Геделя,позволяющая избежать указанного парадокса: для любого высказывания Р и любого множества А существует множество, состоящее из тех и только тех элементов множества А, для которых высказывание Р(х) является истинным, то есть форма задается в виде {xÎA: P(x)}.

В приложении мы приведем набор аксиом, используемых в теории множеств.

Задачи.

1) Равны ли множества:

a) {{1, 2}, {2, 3}} и {1, 2, 3};

b) {{1, 2}} и {1, 2};

c) {x: xÎN и x < 5} и {x: xÎN и (x+1)² < 29}.

2) Верно ли, что {1, 2}Î{{1, 2, 3}, {1, 3}, 1, 2}.

3) Привести пример множеств A, B, C: AÎB, BÎC, но AÏC.

4) Доказать, что для всех a, b, c, d равенство {{a}, {a, b}} = {{c}, {c, d}} выполняется тогда и только тогда, когда a = c и b = d.

Задачи.

1. Доказать следующие утверждения:

а) из АÍВ вытекает, что АÇВ = А и АÈВ = В;

б) из АÇВ = А вытекает, что АÍВ;

в) из АÈВ = В вытекает, что АÍВ.

2. Доказать:

а) АÈ(ВÇС) = (АÈВ)Ç(АÈС);

б) АÇ(ВÈС) = (АÇВ)È(АÇС).

3. Доказать включения:

а) (АÇС)È(ВÇD)Í(АÈВ)Ç(СÈD);

б) (В – С) – (В – А)ÍА – С;

в) А – СÍ(А – В)È(В – С).

4. Доказать: АDВ = (АÈВ) – (АÇВ).

5. Верны ли утверждения для любых множеств А, В, С: 1) если АÍВ и ВÎС, то АÎС; 2) если А ¹ В и В ¹ С, то А ¹ С?

6. При каких условиях на А и В выполняется равенство (А – В)ÈВ = А.

7. Пусть U={a, b, c, d, e, f} – универсум, A = {a, b, c}, B = {a, c, e, f}, C = {d, e, f}. Найти А – В, В – С, С – В, А – С, А^CÈВ, ВÇА^C, АÇС, СDА.

8. Пусть АÇВ = Æ. Что можно сказать про множества А – В и В – А.

9. Пусть АÇВ^С = Æ. Что можно сказать про множества АÇВ и АÈВ.

10. Доказать равенства:

а) (А – В) – С = (А – С) – (В – С);

б) (А – В)È(В – С)È(С – А)È(АÇВÇС) = АÈВÈС;

в) А – В = А – (АÇВ) = (АÈВ) – В;

г) А – (А – В) = АÇВ;

д) А – (ВÈС) = (А – В)Ç(А – С);

е) А – (ВÇС) = (А – В)È(А – С);

ж) (АÈВ) – С = (А – С)È(В – С).

11. Вытекает ли из А – В = С, что А = ВÈС?

12. Вытекает ли из А = ВÈС, что А – В = С?

13. Пусть А – заданное множество, про другое множество Х известно, что АDХ = А. Доказать, что Х = Æ.

14. Доказать равенства:

а) АD(ВDD) = (АDВ)DD;

б) АÇ(ВDD) = (АÇВ)D(АÇD);

в) АDА = Æ;

г) АDÆ = А.

15.Доказать следующие тождества:

а) (АÇВ)È(СÇD) = (АÈС)Ç(ВÈС)Ç(АÈD)Ç(ВÈD);

б) (АÈВ)ÇА = (АÇВ)ÈА = А;

в) А – (В – С) = (А – В)È(АÇС);

г) АÇ(В – С) = (АÇВ) – (АÇС) = (АÇВ) – С;

д) АÈВ = АÈ(В – А);

е) (А^С)^С = А;

ж) АÈА^С = U;

з) АÇА^С = Æ;

и) [А^СÈВ]ÇА = АÇВ;

к) АÇ(В-А) = Æ;

л) А – (ВÈС) = (А – В) – С.

16.Доказать, что

а) (АÈВ)ÇС = АÈ(ВÇС) Û АÍС;

б) А = В Û АDВ = Æ;

в) АÇВ = АÈ В Û А = В;

г) (АÈВ) – В = А Û АÇВ = Æ;

д) (А – В)ÈВ = А Û ВÍА;

е) (АÇВ)ÈС = АÇ(ВÈС) Û СÍА;

ж) АÍВ Þ АÈСÍВÈС;

з) АÍВ Þ АÇСÍВÇС;

и) АÍВ Þ (С-В) Í(С-А);

к) АÍВ Þ В^СÍА^С;

л) А = В^С Û АÇВ=Æ и АÈВ = U.

17.Доказать тождества:

а) АÈВ = АÈВÈ(АÇВ);

б) А – В = А – (АÇВ);

в) АÈÆ = А;

г) А – А = Æ;

д) ADU = A^C;

е) АDВ = (АÈВ) – (АÇВ);

18. Пусть A Í U, B Í U. Доказать:

а) A – B = A Ç B^C;

б) ADB = (A Ç B^C) È (A^C Ç B).

19. Решить систему уравнений

а)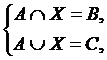

где А, В, С – данные множества и В Í А Í С.

б)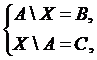

где А, В, С – данные множества и В Í А , АÇС = Æ.

в)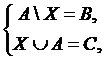

где А, В, С – данные множества и В Í А Í С.

20. Определить операции È, Ç, \ через:

а) Ç и D;

б) D и È;

а) \ и D.

21. Доказать, что для любых множеств E, F, G, H справедливы

включения:

а) ED(FÈG) Ì (EDF)È(EDG);

б) ED (F – G) Ê (FDE) – (GDE);

в) (EDF)Ç(GDH) Ì (EÇG)D(FÇH);

г) (EDF)-(GDH) Ì [ED(F-H)]È[(E-G)D(FÇH)];

д) ED(FÇG) É (EDF)Ç(EDG);

е) (FÇE)D(GÇH) Í (GDE)È(FDH).

22. Справедливо ли равенство

(АDВ)Ç(СDD) = (АÇС)D(ВÇD)?

23. Справедливо ли равенство

(АDВ)È(СDD) = (АÈС)D(ВÈD)?

Задачи.

1. Доказать, что существуют А, В и С такие, что

а) А´В ¹ В´А;

б) А´(В´С) ¹ (А´В) ´С.

2. Доказать, что если А, В, С и D не пусты, то

а) АÍВ и СÍD Û А´СÍВ´D;

б) А=В и С=D Û A´C = B´D.

3. Доказать, что

а)(АÇВ)´(СÇD) = (А´С)Ç(В´D);

б)(А´В)È(C´D) Í(AÈC)´(BÈD);

в)(АÈВ)´С=(А´С)È(В´С);

г)А´(ВÈС)=(А´В)È(А´С);

д)(АÈВ)´(CÈD)=(A´C)È(B´C)È(A´D)È(B´D);

е)(А-В)´С=(А´С)-(В´С);

ж)А´(В-С)=(А´В)-(А´С);-

з)А´В=(A´D)Ç(C´B), где АÍС и BÍD.

4. Найти область определения и область значений для отношений:

а) R={(x,y): x, yÎN и x делит y};

б) R={(x,y): x, yÎN и y делит x};

в) R={(x,y): x, yÎR и x+y ³0};

г) R={(x,y): x,yÎR и 2x>3y}.

5. Пусть R, S, T - некоторые отношения. Проверить справедливость равенств:

а) Ro(SoT) = (RoS)oT;

б) (R^-1)^-1 = R;

в) (RoS)^-1 = S^-1oR^-1.

6. Пусть на множестве А заданы отношения R₁ и R₂. Доказать:

а) если отношения R₁ и R₂ рефлексивны, то рефлексивны отношения R₁ÈR₂, R₁ÇR₂, R₁^-1, R₁oR₂;

б) если отношения R₁ и R₂ иррефлексивны (т.е. для " хÎ А не выполняется хRх), то иррефлексивны R₁È R₂, R₁ÇR₂, R₁^-1, суперпозиция R₁оR₂ может быть иррефлексивной;

в) если отношения R₁ и R₂ симметричны, то симметричны отношения R₁ÈR₂, R₁ÇR₂, R₁^-1, R₁oR₂^-1;

г) отношение R₁oR₂, где R₁ и R₂ симметричны, симметрично тогда и только тогда, когда R₁oR₂ = R₂oR₁;

д) если отношения R₁ и R₂ антисимметричны, то антисимметричны R₁ÇR₂, R₁^-1.

7. Пусть А - конечное множество, n - число его элементов. Доказать, что число подмножеств множества А, состоящих из m элементов, где 0£ m £n, равно

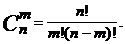
8. Пусть r - отношение, обладающее свойством рефлексивности и транзитивности в множестве А. Определим для а, bÎА отношение R, полагая аRb, если аrb и brа.

а) Доказать, что R есть отношение эквивалентности на А.

в) Доказать, что если аRа', bRb' и аrb, то а'rb'.

9. Во множестве Z⁺´Z⁺ положим по определению (а, b)r(с, d), если а+d=b+с. Доказать, что r является отношением эквивалентности на данном множестве.

«Понятие функции такое же основное, как и понятие множества» Хаусдорф

Функция

Пусть Х и У два множества и F отношение в Х´У.

Определение. Отношение F называется функциейиз Х в У, если оно удовлетворяет свойству:

из xFy и xFz следует, что y = z.

В дальнейшем мы будем применять также обозначение y = F(x) вместо xFy, если F является функцией. Множества D_F и R_F , введенные в предыдущем пункте для функции F носят соответственно названия: D_F - область определенияи R_F - область значенийфункции F. Очень часто область определения и область значений заранее не задаются, а возникают, исходя из задания функции.

Примеры.

1) {(1,2), (2,2), (Рузвельт, Черчилль)};

2) {(1,2), (1,3), (2,2)};

3) {(x, x² +x+1)|xÎR};

4) {(x² ,x)|xÎR}.

Из приведенных примеров 1 и 3 определяют функцию, а 2 и 4 не являются функцией, т.к. не выполнено определение функции.

Для функции применяются также другие названия: преобразование, отображение, соответствие. Если y = F(x), то x называют аргументомфункции, а y образом.

Две функции F и G считаются равными, если выполнены равенства соответствующих множеств. Последнее эквивалентно следующим двум равенствам:

D_F =D_G и F(x)=G(x) для "xÎD_F.

Следующие определения переносятся с отношений:

1) В случае, когда D_F = Х функцию называют всюду определенной.

2) Функция F из Х в У называется сюръекцией(или отображением на), если R_F =У.

3) Функция F из Х в У называется инъекцией(или однозначным отображением), если из х₁ ¹ х₂ следует, что F(х₁) ¹ F(х₂).

Всюду определенная функция F из Х в У называется биекцией, если она одновременно является сюръекцией и инъекцией.

Примеры: 1) функция у=е^x - биекция из R в R₊ ;

2) у=х² - сюръекция из [-1, 1] на [0, 1], не являющаяся инъекцией.

Определение. Пусть F - функция из X в Y, а G - из Y в Z. Суперпозицией функцийF и G называется такая функция H из X в Z, что z = H(x) (т.е. (x, z)Î H Í X´Z) тогда и только тогда, когда y=F(x) и z=G(y). Суперпозиция обозначается GoF. В определении Н – функция, почему?

Определение. Для функции F из Х в У функция G из У в Х называется правой обратной(соответственно, левой обратной), если справедливо равенство FoG=I_У (соответственно, GoF=I_Х), где через I_Х (I_У) обозначено тождественное отображение на Х (соответственно на У), т.е. I_Х(x) = x (I_У(y) = y).

Функция у=х², из рассмотренного выше примера не имеет левой обратной, но имеет правую обратную (ею является функция х= 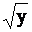). Однако если сузить область определения функции у=х² до отрезка [0,1] (или [-1,0]), оставив туже самую область значений, то эта функция будет иметь уже и левую обратную: х= 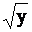(соответственно, х= - ).

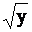Лемма 1. Если функция F имеет левую обратную, то F является инъекцией.

Доказательство. Действительно, если бы F не являлась инъекцией, то существовали бы х₁ ¹ х₂ такие, что y=F(x₁)=F(x₂). Пусть G - левая обратная к F, то x₁ = GoF(x₁ ) = G(y) = GoF(x₂ ) = x₂, что противоречит предположению.

Лемма 2. Если функция F имеет правую обратную, то F является сюръекцией.

Доказательство. Утверждение легко вытекает из определения правой обратной функции G: для любого уÎУ Þ FoG(у)=у.

Лемма 3. Если у функции F из Х в У существуют левая и правая обратная функции, то они совпадают.

Доказательство. Пусть G и H - обозначают соответственно левую и правую обратную функции к F. Тогда D_G = R_F = D_H = У. Остается проверить равенство G(y) = H(y) для любого yÎУ. Но G(y) = G(I_У(y)) = G(F(H(y))) = I_Х(H(y)) = H(y).

Определение. Функция из У в Х, которая является правой и левой обратной к функции F, называется обратной функциейк F и обозначается через F ^-1.

Теорема. Пусть F является функцией из Х в У. Для существования обратной функции F^-1 из У в Х необходимо и достаточно, чтобы F была биекцией.

Необходимость легко вытекает из лемм 1 и 2.

Достаточность. Пусть yÎУ. Так как F является сюръекцией, то существует хÎХ такое, что F(x)=y. При этом такое х одно, так как F также и инъекция. Определим функцию G(x)=y. Легко проверить, что таким образом определенная функция является обратной к F.

Следствие. Если F является биекцией, то и F^-1 также является биекцией.

Задачи.

1. Установить, что следующие отношения являются функцией:

а) вÎУ, R = X´{в}ÍX´У (постоянное отображение);

б) R = {(x, x): xÎX}ÍX´X (тождественное отображение I_X);

в) R = {((x, y), x)}Í(X´Y)´X ( проекция на Х);

г) R = {((x, y), у)}Í(X´Y)´Y ( проекция на Y).

2. Пусть А - произвольное множество из области определения функции f(х). Верно ли равенство f ^-1 [f(A)] = A всегда ?

3. Пусть В - произвольное множество из области значений функции f(х). Верно ли равенство: f[f ^-1 (B)] = B всегда ?

4. Верны ли равенства:

f(AÈB) = f(A)Èf(B);

f(AÇB) = f(A)Çf(B)?

5. Верно ли, что f(R – А) = f(R) – f(А), где R - область определения функции?

6. Пусть А и В - два множества из области значений функции у = f(х). Верны ли равенства:

f ^-1 (AÇB) = f ^-1 (A)Çf ^-1 (B),

f ^-1 (AÈB) = f ^-1 (A)Èf ^-1 (B)?

7. Пусть L - область значений функции у = f(х), а АÍL. Справедливо ли равенство: f ^-1 (L – A) = f ^-1 (L) – f^-1 (А)?

8. Задана функция f: х ® х² + рх + q и интервал (a, b). Определить множество f ^-1 ((a, b)).

9. Задана функция f из А в В. Доказать, что для всякого МÍВ справедливо включение f[f ^-1 (M)] Í M. Пусть Е ÍА. Доказать, что f^-1 [f(E)] ÊE.

10. Задана функция f из А в В. Пусть Е₁ ÍА, Е₂ ÍА, М₁ ÍВ, М₂ ÍВ. Доказать, что если Е₁ ÍЕ₂ , то f(Е₁)Íf(Е₂), если М₁ ÍМ₂, то f ^-1 (М₁) Í f ^-1(М₂).

11. Задана функция f из А в В. Доказать, что следующие условия попарно эквивалентны:

а) f - инъекция;

б) f ^-1 (f(Е)) = Е для любого ЕÍА;

в) f(ЕÇМ) = f(Е)Çf(М) для любых Е, МÍА;

г) f(Е)Çf(М) = Æ для любой пары множеств ЕÍА, МÍА такой, что ЕÇМ= Æ;

д) F(Е – М) = f(Е) – f(М) для любой пары множеств ЕÍА, МÍА такой, что МÍЕ.

12. Пусть даны множества А, В, С, D и функции

f: А ® В, g: В ® С, h: С ® D.

Доказать, что если каждая из суперпозиций gof и hog есть биекция, то и все функции f, g и h являются биекциями.

13. Пусть А - конечное множество и f функция из А в А. Доказать, что

а) если f является сюръекцией, то f также и инъекция;

в) если f является инъекцией, то f также и сюръекция.

14. Построить отношения, удовлетворяющие следующим требованиям:

а) рефлексивное, симметричное, не транзитивное;

б) рефлексивное, транзитивное, не симметричное;

в) симметричное, транзитивное, не рефлексивное.

Задачи.

1. Можно ли сказать, что если А = В, то А и В равномощны, и наоборот, если А и В равномощны, то А=В?

4. Доказать, что для любых трех конечных множества А, В, С справедливо равенство, называемое формулой включения и исключения:

card(AÈBÈC) = card(A)+card(B)+card(C) – card(AÇB) – card(AÇC) – card(BÇC) +card(AÇBÇC).

Континуум

Если рассмотреть любое конечное множество и любое его собственное (непустое и не совпадающее с ним самим) подмножество, то элементов в подмножестве меньше, чем в сам множестве, т. е. часть меньше целого.

Обладают ли бесконечные множества таким свойством? И может ли иметь смысл утверждение, что в одном бесконечном множестве "меньше" элементов, чем в другом, тоже бесконечном? Ведь про два бесконечных множества мы можем пока только сказать, эквивалентны они или нет. А существуют ли вообще неэквивалентные бесконечные множества?

Приведём забавную фантастическую историю из книги Н. Я. Виленкина "Рассказы о множествах". Действие происходит в далёком будущем, когда жители разных галактик могут встречаться друг с другом. Поэтому для всех путешествующих по космосу построена огромная гостиница, протянувшаяся через несколько галактик.

В этой гостинице бесконечно много номеров (комнат), но, как и положено, все комнаты пронумерованы, и для любого натурального числа n есть комната с этим номером.

Однажды в этой гостинице проходил съезд космозоологов, в котором участвовали представители всех галактик. Так как галактик тоже бесконечное множество, все места в гостинице оказались занятыми. Но в это время к директору гостиницы приехал его друг и попросил поселить его в эту гостиницу.

"После некоторых размышлений директор обратился к администратору и сказал:

– Поселите его в № 1.

– Куда же я дену жильца этого номера? – удивлённо спросил администратор.

– А его переселите в № 2. Жильца же из № 2 отправьте в № 3, из № 3 – в № 4 и т. д."

Вообще, пусть постоялец, живущий в номере k, переедет в номер k+1, как это показано на следующем рисунке:

Тогда у каждого снова будет свой номер, а № 1 освободится.

Таким образом, нового гостя удалось поселить – именно потому, что номеров в гостинице бесконечно много.

Первоначально участники съезда занимали все номера гостиницы, следовательно, между множеством космозоологов и множеством Nбыло установлено взаимно однозначное соответствие: каждому космозоологу дали по номеру, на двери которого написано соответствующее ему натуральное число. Естественно считать, что делегатов было "столько же", сколько имеется натуральных чисел. Но приехал ещё один человек, его тоже поселили, и количество проживающих увеличилось на 1. Но их снова осталось "столько же", сколько и натуральных чисел: ведь все поместились в гостиницу!

Мы пришли к удивительному выводу: если к множеству, которое равномощно N, добавить ещё один элемент, получится множество, которое снова равномощно N. Но ведь совершенно ясно, что делегаты-космозоологи представляют собой часть того множества людей, которые разместились в гостинице после приезда нового гостя. Значит, в этом случае часть не "меньше" целого, а "равна" целому!

Итак, из определения эквивалентности (которое не приводит ни к каким странностям в случае конечных множеств) следует, что часть бесконечного множества может быть эквивалентна всему множеству.

Новый постоялец не удивился, когда на другое утро ему предложили переселиться в № 1000000. Просто в гостиницу прибыли запоздавшие космозоологи из галактики ВСК-3472, и надо было разместить ещё 999999 жильцов.

Но потом произошла какая-то накладка, и в эту же самую гостиницу приехали на съезд филателисты. Их тоже было бесконечное множество – по одному представителю от каждой галактики. Как же их всех разместить?

Эта задача оказалась весьма сложной. Но и в этом случае нашёлся выход.

"В первую очередь администратор приказал переселить жильца из № 1 в № 2.

– А жильца из № 2 переселите в № 4, из № 3 – в № 6, вообще, из номера n – в номер 2n.

Теперь стал ясен его план: таким путём он освободил бесконечное множество нечётных номеров и мог расселять в них филателистов. В результате чётные номера оказались занятыми космозоологами, а нечётные – филателистами... Филателист, стоявший в очереди n-м, занимал номер 2n-1". И снова всех удалось разместить в гостинице. Итак, ещё более удивительный эффект: при объединении двух множеств, каждое из которых равномощно N, вновь получается множество, равномощное N, т. e. даже при "удвоении" множества мы получаем множество, эквивалентное исходному!

Определение. Множество А, равномощное множеству натуральных чисел N, называется счетным множеством(имеет мощность счетного множества). Если множество В является бесконечным и не равномощно множеству N, то его называют несчетным.

Множество, которое является конечным или счетным, еще называют не более чем счетным.

Пусть множество А является счетным. По определению, тогда существует биекция А на N, т.е. каждому аÎА соответствует единственный номер nÎN и множество А обращается в некоторую последовательность {а_n}.

Теорема 1. Любое подмножество счетного множества не более чем счетно.

Доказательство. Пусть А = {a_n} - счетное множество и В Í А. Если В конечное множество, то утверждение доказано. Предположим, что В бесконечное множество. Те элементы А, которые попали в В будут иметь некоторые номера в порядке возрастания: 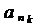. Тогда необходимая нам биекция, показывающая, что В является счетным множеством, задается в виде: 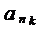® k.

Теорема 2. Объединение конечного или счетного числа счетных множеств является счетным множеством.

Доказательство. Рассмотрим счетное объединение счетных множеств (случай конечного является частным). Итак, пусть А_n - счетные множества для любого nÎN и А = È_n А_n. Для доказательства нам необходимо указать биекцию множества А на множество N, т.е. указать каждому аÎА его номер. Запишем все множества А в виде последовательностей с двумя индексами, где первый указывает номер множества. Зададим закон, который каждому элементу А ставит в соответствие некоторый порядковый номер. Если элементы множества А_n обозначить через а_nk, то высотой элемента а_nk назовем число n + k. Перепишем элементы множества А, располагая все его элементы по следующему правилу - сперва перепишем все элементы высоты 2, затем высоты 3, 4 и т.д: а₁₁, а₁₂, а₂₁, а₁₃, а₂₂, а₃₁, а₁₄, а₂₃, а₃₂, а₄₁, ... Тогда любой элемент множества А будет иметь определенный номер.

Теорема 3. Любое бесконечное множество содержит счетное подмножество.

Доказательство. Выберем в заданном множестве А какой-либо элемент, придав ему единичный индекс: а₁. Среди всех оставшихся элементов множества А найдется не равный а₁ элемент (в силу бесконечности А). Его мы обозначим через а₂. Продолжая этот процесс до бесконечности мы получим необходимое нам счетное множество {a_n} .

Теорема 4. Пусть множество М - несчетно, множество А не более чем счетно и А Í М. Тогда множество М – А равномощно множеству М.

Доказательство. Пусть множество М – А не более чем счетно. Тогда множество М = АÈ(М – А) по теореме 2 не более чем счетно. Это противоречит тому, что множество М несчетно и, следовательно, наше исходное предположение не верно. Таким образом, множество М – А несчетно. Последнее еще не означает равномощности множеств М и М – А. Докажем ее. Выделим из М – А счетное множество В. Обозначим через С множество С = (М – А) – В. Справедливы равенства М = АÈВÈС и М – А = ВÈС. Множество АÈВ счетно (теорема 2). Следовательно, существует биекция f из АÈВ на А. Теперь можно построить биекцию g из М на М – А по правилу:

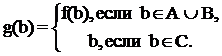
Теорема 5. Если множество С бесконечно, а В не более чем счетно, то множество ВÈС равномощно множеству С.

Доказательство. Если множество С счетно, то множество ВÈС также счетно и следовательно они равномощны. Если же множество С не счетно, то мы можем воспользоваться теоремой 4, положив в ней А = СÇВ, а М = С.

Теорема 6. Если множество С является бесконечным, то существует его подмножество В такое, что В¹С и В равномощно с С.

Доказательство. По теореме 3 мы можем выделить из множества С его счетное подмножество А. Если множество С счетно, то в качестве В из утверждения теоремы можно взять В=А. Если же С не счетно, то можно положить В=С-А и утверждаемое вытекает из теоремы 4.

Теорема 7. Множество рациональных чисел Q является счетным.

Доказательство. Обозначим через Р множество всех пар натуральных чисел (p, q), таких что p и q не имеют общих целых делителей, кроме единицы. Для пары натуральных чисел (p, q) введем ее высоту m = p + q. Обозначим Р_n множество пар натуральных чисел высоты n. Нетрудно проверить, что каждое множество Р_n является конечным и содержит не более, чем n-1 член. Так как Р = È_n Р_n, то множество Р счетно в силу теоремы 2.

Рассмотрим теперь множество Q₊ положительных рациональных чисел. Каждое положительное рациональное число представим в виде не сократимой дроби p/q. Тогда между этим числом и парами из Р существует биекция p/q « (p,q), которая показывает равномощность множеств Q ₊и Р, т.е. счетность множества Q₊. Ясно, что множества Q₊ и Q _- равномощны. Тогда Q = Q ₊ÈQ _- является счетным множеством как объединение двух счетных множеств.

Теорема 8. Множество точек интервала (0,1) является несчетным.

Доказательство(диагональный метод Кантора).Доказательство проведем от противного, предположив, что множество точек интервала (0,1) является счетным. Тогда все точки можно записать в виде последовательности:

0,а₁₁а₁₂а₁₂а₁₄ ...

0,а₂₁а₂₂а₂₃а₂₄ ...

0,а₃₁а₃₂а₃₃а₃₄ ...

0,а₄₁а₄₂а₄₃а₄₄ ...

..........................

Покажем, что на самом деле здесь записаны не все числа из интервала (0,1). Построим число 0,а₁а₂а₃а₄ ... по правилу а_k ¹ а_kk . Это всегда можно сделать. Но тогда построенное нами число входит в интервал (0,1) и не совпадает ни с одним из записанных чисел. Мы получили противоречие с тем, что нами были выписаны все числа из интервала (0,1) и этим доказали теорему.

Множества, равномощные множеству точек интервала (0, 1), называются множествами мощности континуум.

Задачи.

1. Показать, что если множества А и В являются счетными, то и их произведение А´В является счетным.

2. Установить биекцию между множеством N всех натуральных чисел и множеством Q всех четных положительных чисел.

3. Установить биекцию между множеством N всех натуральных чисел и множеством Р всех четных чисел.

Сравнение мощностей

Теорема 1 (Кантора-Бернштейна).Пусть для множеств А и В существуют множества А₁ ÍА и В₁ ÍВ такие, что множество А равномощно с В₁, а множество В с А₁, то множества А и В равномощны.

Доказательство. Пусть f - биекция В на А₁, а g - биекция А на В₁. Тогда f(В)=А₁ и f(В₁)=А₂ ÍА₁. Суперпозиция h=fog функций является также биекцией А на А₂. Тогда функция h отображает

А на А₂

А₁ Í А на А₃ Í А

А₂ Í А₁ на А₄ Í А₃

А₃ Í А₂ на А₅ Í А₆ и т.д.

Отсюда следует, что h является биекцией

из А – А₁ на А₂ – А₃

из А₁ – А₂ на А₃ – А₄

из А₂ – А₃ на А₄ – А₅ и т.д.

Зададим множества

Е = (А – А₁)È(А₂ – А₃)È(А₄ – А₅)È(А₆ – А₇)È ...

F = (А₂ – А₃)È(А₄ – А₅)È(А₆ – А₇)È ...

D = АÇА₁ÇА₂ÇА₃ÇА₄Ç...

G = (А₁ – А₂)È(А₃ – А₄)È(А₅ – А₆)È ...

Из замеченного выше следует, что h является биекцией E на F. Кроме того, справедливы равенства А = DÈGÈE и А = DÈGÈF. Следовательно отображение Т из А в А₁, определяемое соотношением

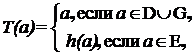
является биекцией А на А₁, т.е. множества А и А₁ равномощны. Последнее означает, что все четыре множества в теореме равномощны.

Теорема 2. Пусть Х и У два множества такие, что Х¹Æ, У¹Æ и в У не менее двух элементов. Тогда множество всех функций, действующих из Х в У является множеством, мощность которого больше мощности множества Х.

Доказательство. Обозначим множество функций, действующих из Х в У через У^Х. Доказательство разобьем на две части. Сперва покажем, что существует инъекция множества Х на часть множества У^Х. Пусть у₁ÎУ, у₂ÎУ, у₁ ¹ у₂ и х₀ÎХ. Построим функцию f[х₀] следующим образом: f[х₀](х₀) = у₁, а если х ¹ х₀, то f[х₀] (х) = у₂. При таком построении различным элементам в Х соответствуют различные функции. Например, если х₁ ¹ х₀, то f[х₁](х₀) = у₂. Таким образом, получаем инъекцию из Х в У^X.

Покажем теперь, что не существует биекции между Х и У^X. Предположим противное, что g является биекцией из Х на У^X и g(x) = f^x ÎУ^Х

Наши рекомендации