Структурированные типы данных. программирование алгоритмов обработки массивов
Массив – это упорядоченная последовательность данных одного типа, имеющих одно имя. Массив описывается следующим образом:
<тип> <имя массива> [n1] [n2]…
где n1, n2 – размер массива по данному измерению.
Элемент массива представляет собой индексированную переменную, индекс которой указывается в квадратных скобках. Индекс может быть целой константой, целой переменной или выражением целого типа. Все массивы индексируются с нуля.
Массивы подобно переменным могут быть инициализированы начальными значениями, например.
float a[3]={1.2, 3.4, -0.1};
где a[0]=1.2, a[1]=3.4, a[2]=-0.1.
Имя массива является константой указателем на адрес первого элемента массива. Начальный адрес массива определяется компилятором в момент описания массива и не может быть переопределен.
Наиболее серьезная и распространенная ошибка при работе с массивами – выход за границу массива, т.е. когда предпринимается попытка записать или прочитать значение по адресу памяти, который не был описан в программе.
Массивы хранятся в памяти как сплошные последовательности компонентов, причем быстрее изменяется дальний правый индекс.
Обращение к элементу массива производиться указанием имени массива и индексов, заключенных в квадратные скобки:
<имя>[<индекс>]
В данном типе определена единственная операция присваивания. Можно присваивать массив лишь массиву, например: А=С. Операции сравнения производиться только поэлементно.
При работе с массивами выделяют следующие типовые операции:
1. Заполнение массива возможно либо с помощью генератора случайных чисел (random()), либо с клавиатуры, либо по определенному правилу.
Пример.
for (i=0; i<n; i++)
for (j=0; j<n; j++)
cin>> a [i][j];
В квадратной матрице выделяют главную и побочную диагонали, относительно которых элементы могут находиться выше или ниже (рис. 5).
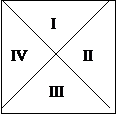
Рис. 5. Принятое деление матрицы на четверти.
Условия нахождения элементов в каждой из частей матрицы следующие:
1. I: (i<j) && (i+j<n-1)
2. II: (i<j) && (i+j>n-1)
3. III: (i>j) && (i+j>n-1)
4. IV: (i>j) && (i+j<n-1)
5. на главной диагонали: i = = j
6. на побочной диагонали: i+j = = n-1
где i – номер строки, j – номер столбца, в которых находится элемент матрицы, n – размерность квадратной матрицы.
2. Вычисление суммы, произведения, среднего арифметического, среднего геометрического, количества элементов, удовлетворяющих некоторому условию.
Пример. Вычислить сумму положительных элементов матрицы и количество отрицательных элементов.
for (i=0; i<n; i++)
for (j=0; j<n; j++)
{if a[i][j]>0 s+=a[i][j];
else k++;
}
3. Сортировка массива
Идея метода сортировки выбором состоит в том, чтобы создавать отсортированную последовательность путем присоединения к ней одного элемента за другим в правильном порядке.
Шаги алгоритма:
1. находим минимальное значение в текущем списке;
2. производим обмен этого значения со значением на первой позиции;
3. сортируем хвост списка, исключив из рассмотрения уже отсортированный первый элемент.
Будем строить выходную последовательность, начиная с левого конца массива. Алгоритм состоит из n последовательных шагов, начиная с нулевого и заканчивая (n-1)-м.
На i-м шаге выбираем наименьший из элементов x[i] ... x[n] и меняем его местами с x[i]. Последовательность шагов при n=5 изображена на рис. 6.
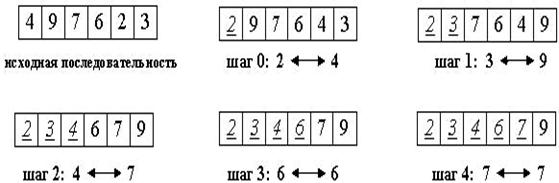
Рис. 6. Сортировка выбором.
Вне зависимости от номера текущего шага i, последовательность x[0]...x[i] (выделена курсивом) является упорядоченной. Таким образом, на (n-1)-м шаге вся последовательность, кроме x[n], оказывается отсортированной, а x[n] стоит на последнем месте по праву: все меньшие элементы уже ушли влево.
Пример программной реализации.
for (i = 0; i < n-1; i++) { min = i; for (j = i+1; j < n; j++) { if (x[min] > x[j]) { // сортировка по убыванию min = j; } } temp = x[i]; x[i] = x[min]; x[min] = temp;}4. Вставка и удаление элементов массива
Удаление одного элемента из массива происходит по следующей схеме:
- указывается или ищется порядковый номер элемента, который необходимо удалить из массива;
- все элементы, стоящие за удаляемым элементом, сдвигаются на одну позицию влево;
- количество элементов уменьшается на единицу.
for (i=0; i<n; i++) // n – номер удаляемого элемента
a[j]=a[j+1];
k-=1; // количество элементов
Пример.Найти значение и номер наименьшего элемента в массиве.
Алгоритм решения задачи показан на рис.7.
#include <stdio.h> // библиотека, содержащая описание
// операторов ввода/вывода
# include <conio.h> // библиотека, содержащая описание
// операторов для работы с экраном
# include <stdlib.h> // библиотека, содержащая описание
// генератора случайных чисел
void main() // заголовок главной функции программы
{int a*, i, min, n; // описание целых переменных
clrscr(); // очистка экрана
cout<<”Input size of array”; // вывод информационного сообщения
cin>>n; // ввод размерности массива
randomize(); // генератор случайных чисел, инициализация
// первого элемента ряда
for(i=0;i<n;i++) // заполнение массива
{
a[i]=random(100);
cout<<” ”<<a[i]; // вывод содержимого массива на экран
}
min=a[0];
for (i=0;i<n;i++) // поиск минимального элемента
if (a[i]<min)
{ min=a[i];
k=i;
}
cout<<endl<<”min=”<<min<<” k=”<<k; // вывод результатов
getch();
}
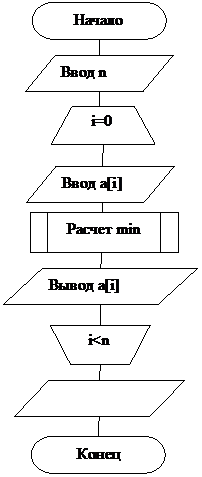 | 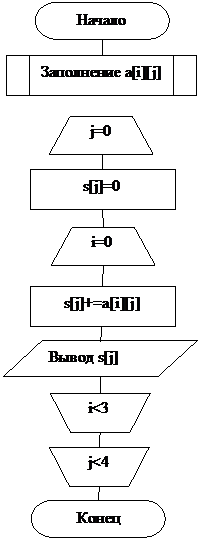 |
Рис.8
Пример. Вычислить сумму элементов в столбцах двумерного числового массива а размером [3][4].
Алгоритм показан на рисунке 9.
#include <stdio.h> // библиотека, содержащая описание
// операторов ввода/вывода
# include <conio.h> // библиотека, содержащая описание
// операторов для работы с экраном
# include <stdlib.h> // библиотека, содержащая описание
// генератора случайных чисел
void main() // заголовок главной функции программы
{int a[3][4], i, j, sum[4]; // описание переменных
clrscr(); // очистка экрана
randomize(); // генератор случайных чисел, инициализация
// первого элемента ряда
for(i=0;i<3;i++) // заполнение массива
{for(j=0;j<4;j++)
{
a[i][j]=random(100);
cout<<” ”<<a[i][j]; // вывод матрицы на экран
}
cout<<endl;
}
cout<<endl<<”summa”<<endl;
for(j=0;j<4;j++)
{
sum[j]=0;
for (i=0;i<3;i++) // поиск минимального элемента
{sum[j]+=a[i][j];
cout<<sum[j]; // вывод результатов
}
getch();
}
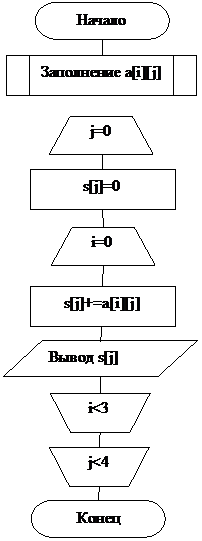
Лабораторная работа 5
