Реализация и исследование модели многомерной системы регулирования

2.1 Постановка задачи и исходные данные

Структурная схема многомерной системы регулирования (в соответствии с вариантом задания №3):

Рис.2.1

Для заданной многомерной системы автоматического регулирования составить математическую модель в виде системы дифференциальных уравнений, устанавливающих взаимосвязь выходных величин y₁(t), y₂(t) с внешними воздействиями g₁(t), g₂(t) и f(t).

Решить полученные дифференциальные уравнения относительно y₁(t), y₂(t) поочередно задаваясь ступенчатым изменением внешних воздействий. Получить графическую иллюстрацию решения.

Построение математической модели

Используя заданную структурную схему и известные передаточные функции сначала составим математическую модель системы в изображениях по Лапласу. В соответствии со структурной схемой рис.2.1 выпишем уравнения связи:

y₁ = W₁₁u₁ – W_ff;

u₁ = g₁ - y₁;

y₂ = W₂₁u₁ + W₂₂u₂;

u₂ = g₂ – y₂.

Подставляя величины u₁ и u₂ в выражения для y₁ и y₂ получим:

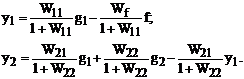
Раскроем выражения для передаточных функций:

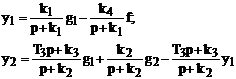
и избавимся от знаменателей:

(p + k₁)y₁ = k₁g₁ – k₄f;

(T₃p + k₃)y₁ + (p + k₂)y₂ = (T₃p + k₃)g₁ + k₂g₂.

Полученные уравнения представляют собою уравнения общего вида:

A(p)×y = B(p) ×g + C(p) ×f,

в котором

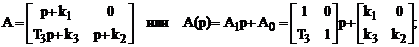
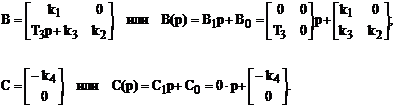
Для получения нормальной формы Коши

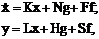
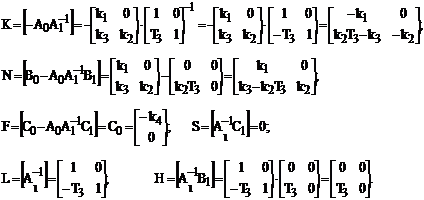
Характеристическое уравнение |A|=0:

p² +(k₁ + k₂)p +k₁k₂ = 0

Для заданных числовых параметров данное характеристическое уравнение имеет положительные вещественные корни. Из чего следует, что решение будет неустойчивым.

Объект системы управляем и наблюдаем, так как r=1=n, согласно критериям Калмана.

По известным матрицам K, N, F, L, H и S составляем описание системы регулирования в нормальной форме Коши:

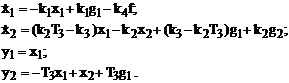
Для численного решения полученной системы воспользуемся уравнениями Эйлера:

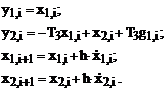
Для последующего исследования динамики системы воспользуемся программным средством Mathcad 15.

Визуализация полученных результатов средствами Mathcad

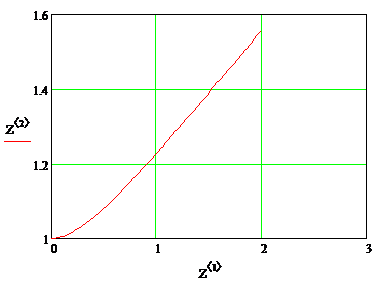
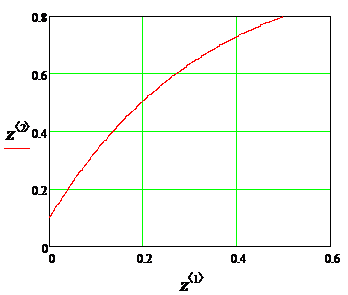
2.3.1 Графическое отображение численных результатов (методом Рунге–Кутта)

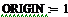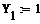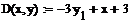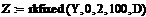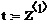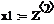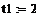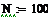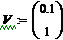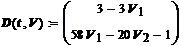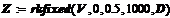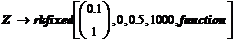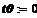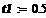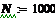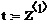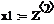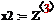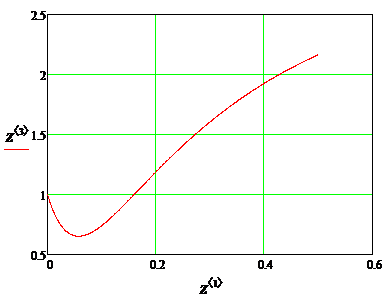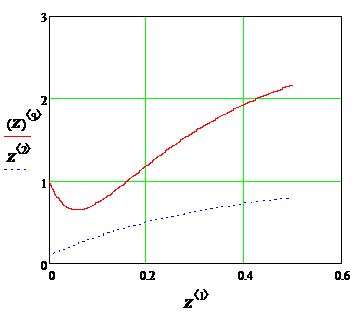2.3.2 Графическое отображение численных результатов (методом Эйлера)

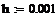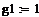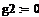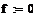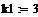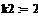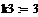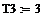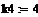шаг интегрирования, задающий временную сетку

пороговое воздействие, равное единичному импульсу

начальное условие для внешнего воздействия

параметры передаточных функций

параметр временной передаточной функции

Цикл, задающий динамическое поведение системы методом Эйлера.

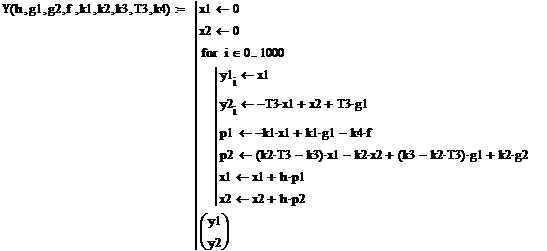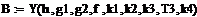Визуальная интерпретация средствами построенных графиков средой MathCad:

Заключение

В процессе выполнения курсовой работы была реализована математическая модель заданной системы.

Анализ математической модели позволил исследовать исходную систему и получить следующий аналитический результат. Данная многомерная система регулирования является неустойчивой. Однако объект управления наблюдаем и управляем. Для того чтобы система приобрела устойчивость необходимо увеличить численные значения параметров передаточных функций, реализованных в усилительном звене (линейно-усилительные блоки в структуре системы).

Целью решения полученных дифференциальных уравнений является изучение реакции выходных величин y₁(t), y₂(t) системы автоматического регулирования на единичные ступенчатые воздействия g₁(t), g₂(t), f(t). Для наглядного представления результатов следует рассмотреть три решения - отдельно для каждого внешнего воздействия: g₁(t)=1₀(t), g₂(t)=0, f(t)=0; g₁(t)=0, g₂(t)=1₀(t), f(t)=0; g₁(t)=0, g₂(t)=0, f(t)= 1₀(t).

Анализ полученных графических результатов выявил характерную особенность, присущую для многомерных систем автоматического регулирования - существование влияния какого-либо из внешних воздействий одновременно на несколько регулируемых величин.

Исходя из этого, при синтезе системы необходимо обеспечить независимость управления каждой выходной величиной.