Булева алгебра и коммутационные схемы

В 1938 г. Клод Шеннон заметил связь между таблицами истинности и электрическими цепями.

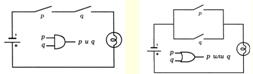
В схеме представленной на левом рисунке лампочка загорается (имеет значение 1) если оба переключателя замкнуты (значения 1), что соответствует высказыванию pq.

В схеме на правом рисунке лампочка загорается (1) если хотя бы один из переключателей замкнут (т.е. хотя бы один имеет значение 1), что соответствует высказыванию p Ú q

Предполагается, что имеется схема в которой лампочка загорается, если выключатель разомкнут.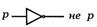

Анализ коммутационных схем

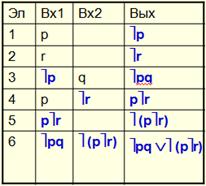
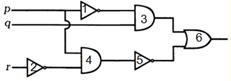
Анализ коммутационных схем заключается в определении булевой формулы соответствующей рассматриваемой схемы

Для этого составляют таблицу, в которой для каждого функционального элемента определяют значения входов и выхода.

Выход последнего элемента определяет итоговую

булевую функцию.

Синтез коммутационных схем

Синтез коммутационных схем заключается в построении схемы по заданной формуле

Пример: Муниципальный совет состоит из 3 человек. Каждый член совета имеет для голосования кнопку «за» и «против». Решение принимается если за него проголосует большинство. Построить коммутационную схему устройства, сигнализирующего о том, что решение принято.

Решение будет принято, если голосование пройдет по любому из вариантов pqr, ùpqr, pùqr, pqùr.Поэтому итоговая булевая функция:pqr Ú ùpqr Ú pùqr Ú pqùr

В дальнейшем, еслиэлементарная конъюнкция состоитиз n переменных,то ее функциональный элементимеет n входов.Аналогичное применяется дляэлементарной дизъюнкции.

Синтез коммутационных схем
Пример

Прежде чем строить коммутационную схему формулу следует максимально упростить, используя карту Карно или закону булевой алгебры pqr Ú ùpqr Ú pùqr Ú pqùr = pq Ú qr Ú pr = pq Ú r (qÚ p)

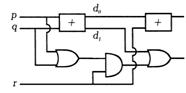
Проектирование полубитного сумматора

Полубитный сумматор складывает два одноразрядных числа (p, q), представленных в двоичном виде. На выходе получают двухразрядное число (d₁d₀), где d0 - первый разряд d1- второй разряд (разряд переноса)

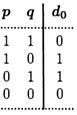
Построим СДНФ для d0 = pù q Ú ù pq, d1=pq

Проектирование полубитного сумматора

Построим схему

d0 = pùqÚùpq, d1=pq.

Можно построить эквивалентную схему, содержащую меньшее число функциональных элементов. Для этого используя булеву алгебру

Проведем упрощение d0

d0 = pùqÚùpq =ùù(pùqÚùpq) =ù(ù(pùq) &ù(ùpq)) =ù((ùpÚq) & (pÚùq)) =ù(pùpÚqpÚùpùqÚqùq) =ù(qpÚùpùq ) =ù(qp) &ù(ùpùq ) = (ùpÚùq ) & (qÚp) =ù(pq ) & (qÚp)