Отношение строго и нестрого порядка

Нестрого порядка: транзитивно, антисимметрично и рефлексивно.

Пример:Отношение « быть не старше» на множестве людей. Если человек А не старше В и В не старше С, то А не старше С (транзитивно). Если А не старше В, то В не старше А, только в случае А=В (антисимметричное). А не старше А, так как не старше подразумевает ≤

Строго порядка транзитивно, антисимметрично и антирефлексивно.

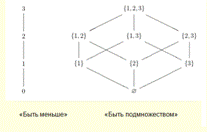
Пример: Отношение «быть меньше» на множестве N. Если a<b и b<c, то a<c (транзитивно). Если a<b, то b<a не верно (асимметрично т.е. антисимметрично и антирефлексивно).

Отношение полного и линейного порядка

Отношение полного (линейного) порядка

для любых a и b ∊ M, если a≠b, то либо (a,b) ∊ R либо (b,a) ∊ R

RÈD_МÈR^-1= U

Пример:рассмотренное нами отношение «быть не старше», заданное на множестве людей.

Если отношение порядка не является полным, то оно является отношением частичного порядка.

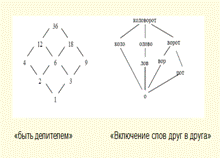
10.Диаграмма Хассе как способ задания отношения частичного порядка на множестве. Непосредственно предшествующие элементы. Линейно упорядоченные подмножества

Диаграммой Хассе для отношения «быть подчиненным»

Диаграмма Хассе задает схему непосредственных предшественников.

Если вершина x является непосредственным предшественником у,

то х помещают на нижнем уровне, а у на верхнем. Вершины

соединяют не направленными дугами.

Замыкание отношений. Рефлексивное, симметричное, транзитивное замыкание отношений.

R* называется замыканием отношения R относительно свойства P (рефлексивности, симметричности, транзитивности), если

R* обладает свойством P;

R Í R*;

R* является подмножеством любого другого отношения, содержащего R и обладающего свойством P.

Рефлексивным замыканием R_D отношения R называется отношение R È D_A.

Симметричным замыканием R_S отношения R называется отношение R È R^#.

Транзитивным замыканием R_t отношения R называется отношение

R_t = R È R² È R³ È… È Rⁿ È…

Понятие нечеткого множества. Функция принадлежности и ее интерпретация. Способы формализации нечетких множеств. Наиболее распространенные параметрические функции принадлежности.

Пусть U— универсальное множество. Множество А Í U задается характеристической функцией, значения которой (0 или 1) указывает на принадлежность x Î U множеству A:

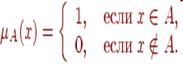
Нечеткие множества – это обобщение обычных множеств, когда характеристическая функция (называемаяфункцией принадлежности) может принимать любые значения на отрезке [0,1]. Значение функции принадлежности m_A(x) называется степенью принадлежности элемента x нечеткому множеству .

Более строго, нечетким множеством называется совокупность пар {(x| m_A(x))}, " x Î U

Пусть, например,

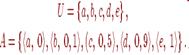
элемент a не принадлежит множеству , элемент b принадлежит ему в малой степени, элемент cболее или менее принадлежит, элемент d принадлежит в значительной степени, e является элементом множества