Операции над множествами и законы алгебры множеств. Диаграммы Эйлера. Формула включений и исключений. Покрытия и разбиения. Классы разбиения.

ОБЪЕДИНЕНИЕМмножеств A и B называется множество

A ÈB = {xïxÎA или xÎB}

ПЕРЕСЕЧЕНИЕМмножеств A и B называется множество

A ÇB = {xïxÎA и xÎB}

РАЗНОСТЬЮмножеств A и B называется множество

A \ B = {xïxÎA и xÏB}

ДОПОЛНЕНИЕМмножества A называется множество

–A = {xïxÎU и xÏB}

СИММЕТРИЧЕСКОЙ РАЗНОСТЬЮмножеств A и B называется множество

A D B = (A \ B)È(B \ A)

A D B = (A È B) \ (B Ç A)

Теорема: ïA È Bï = ïAï + ïBï – ïA Ç Bï

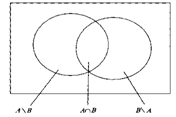
Введем обозначения |А/В|=m, |В/А|=n, |АÇ B|=p.

Тогда, |A|=m+p, |B|=n+p и

|AÈB| = m+n+p = m+p + n+p –p = |A| +|B| - |АÇ B|

Если множество A представляет собой объединение подмножеств А₁, А₂, …, А_n, …, то совокупность {А₁, А₂, …, А_n, …} подмножеств называется покрытиеммножества A

Если подмножества входящие в покрытие такие, что

A_i Ç A_j =Æ при i¹ j, то совокупность {А₁, А₂, …, А_n, …} называется разбиениеммножества A,

а подмножества A_i — классами этого разбиения.

Пример: А={1,2,3}, A1={1}, A2={2}, A3={3}, A4={1,2}, A5={2,3},

A6={3,1},

{A1, A2, A3} - разбиение

{A4, A5, A6} - покрытие

4.Упорядоченная пара, кортеж, декартово произведение множеств. Прямое произведение n множеств, степень множества. Двуместное и n-местное соответствие. Способы задания соответствий. Пустое и полное соответствие.

Упорядоченная пара - запись (a, b), где a Î A , а b Î B.

Кортеж – запись (a1, …,an), где a1 Î A1 ,…, an Î An

Прямое (декартово)произведение двух множеств A и B этомножество всех упорядоченных пар элементов этих множеств A ´ B = { (a,b) | a Î A , b Î B }

Пример: A={a1, a2}, B={b1, b2}, A´B = { (a1,b1), (a1,b2), (a2,b1), (a2,b2) }

Точка на декартовой плоскости задается двумя координатами т.е. упорядоченной парой. Отсюда название – декартово произведение

Теорема: |A ´ B | = |A|∙ |B|

Доказательство: первый компонент упорядоченной пары можно выбрать n=|A| способами, воторой компонент m=|B| способами. Всего имеется |A|∙ |B| упорядоченных пар

Прямое произведение n множеств A1…An этомножество всех кортежей, образованных элементами этих множеств.

A1´…´An = { (a1,..an) | a1 Î A1 , … , an ÎAn }

При этом | A1´…´An| = |A1|∙ … ∙ |An|

Пример: A1={1,2}, A2={a,b}, A3={x,y}. Тогда A1´A2´A3={(1,a,x), (1,a,y), (1,b,x), (1,b,y), (2,a,x), (2,a,y), (2,b,x), (2,b,y)}

Степень n множества А - прямое произведение множества А самого на себя n раз Аⁿ=A´… ´ A (n-раз)

Пример: A={a,b}. Тогда A²={(a,a),(a,b),(b,a),(b,b)}, A³={(a,a,a), (a,a,b), (a,b,a), (a,b,b), (b,a,a), (b,a,b), (b,b,a), (b,b,b)}

Кортеж – запись (a1, …,an), где a1 Î A1 ,…, an Î An

Прямое произведение n множеств A1…An этомножество всех кортежей, образованных элементами этих множеств.

A1´…´An = { (a1,..an) | a1 Î A1 , … , an ÎAn }

При этом | A1´…´An| = |A1|∙ … ∙ |An|

Пример: A1={1,2}, A2={a,b}, A3={x,y}. Тогда A1´A2´A3={ (1,a,x), (1,a,y), (1,b,x), (1,b,y), (2,a,x), (2,a,y), (2,b,x), (2,b,y) }

N-местным соответствием R, заданным на множествах М1, M2, … , Мn называется подмножество R Í M1×М2×…×Мn. При этом элементы, составляющие кортеж, обладают определенным свойством (находятся в соответствии)

Пример: 4-местного отношения: М1- множество групп, М2 - множество предметов, М3 - множество дней недели. М4 - множество пар. Расписание задает 4-местное соответствие R Í M1×М2×М3×М4 – «группа а изучает предмет b в день недели c парой номер d»

Если R = Æ — пустое множество, то соответствие называется пустым.

Если R = M1×М2×…×Мn, то соответствие называется полным.

5.Область определения (прообраз Dom) и область значений (образ Im) соответствия. Образ (im) и прообраз (coim) элемента. Всюду определенное, сюръективное, функциональное и инъективное соответствие. Отображения множества А в (на) множество В, биъективное и взаимнооднозначное соответствие. N-арная функция.

Область определения (прообраз) соответствия Dom R = {a: (a,b) Î R} - это такие элементы а Î A, для каждого из которых найдется хотя бы один элемент b Î B, такойчто (a,b) Î R.

Область значений (образ) соответствия Im R = {a: (a,b) Î R} – этомножество элементов b Î B, для каждого из которых найдется хотя бы один элемент a Î A такой, что (a,b) Î R.

Dom R = {Лена, Петя, Маша, Вася, Женя}

Im R = {Горький, Достоевский, Лермонтов, Некрасов, Пушкин, Толстой, Фет}

Образ a Î А относительно R (im _R a) – это множество элементов b Î B таких, что (a,b) Î R

Прообраз элемента bÎB относительно R (coim _R b) – это множество элементов a Î A таких, что (a,b) Î R

Im R =È_{aÎ A} im _R a, Dom R =È_{bÎ B} coim _R b.

im _R Лена = {Некрасов, Фет} coim _R Горький = {Петя, Женя}

Всюду (полностью) определенное соответствие –это соответствие, у которогоDom R = A (каждый элемент множества А включен в соответствие). В противном случае – частично определенное.

Сюръективное соответствие –это соответствие, у которого

Im R = B (каждый элемент множества В включен в соответствие)

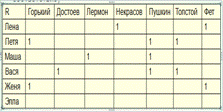
Частично определенное ( элемент Эллочка не имеет образа), Сюръективное

Функциональное соответствие (или функция) –это соответствие, у которогоесли элементa Î A имеет образ при соответствии R, то он единственный элемент bÎB (im _Ra = ! bÎB)

Инъективное соответствие –это соответствие, у которогоесли элементаb Î B имеет прообраз при соответствии R, то он единственный элемент a Î A (coim _R b = ! aÎA)

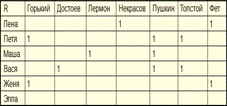
Не функциональное (т.к. im _R Лена = {Некрасов, Фет} )

Не инъективное (т.к. coim _R Горький = {Петя, Женя}

Отображением A в B (F:A→B)называется полностью определенное и функциональное соответствие

Отображением A на B (F:A→B)называется полностью определенное, сюръективное и функциональное соответствие

Биективным соответствиемназывается сюръективное и инъективное соответствие

Взаимнооднозначным соответствиемназывается полностью определенное, сюръективное, инъективное и функциональное соответствие.

Соответствие F, заданное на множествах A₁, A₂, …, A_n, B называется отображением или функцией из A₁ ´ A₂ ´ … ´ A_n в B(F: A₁ ´ A₂ ´ … ´ A_n ® B), если F функциональное и полностью определенное. Число n называют арностью функции F.

Соответствие F называетсячастичным отображением или частичной функцией, если F функциональное и частичное.