Старооскольский технологический институт им. А.А. УГАРОВА
Старооскольский технологический институт им. А.А. УГАРОВА
(филиал) федерального государственного автономного образовательного учреждения
высшего профессионального образования
«Национальный исследовательский технологический университет «МИСиС»
Кафедра АИСУ
Симонова А.Г., Лазарева Т.И., Михайлюк Е.А.
Компьютерное
Обеспечение специальности
Рабочая тетрадь
По выполнению домашних работ
для студентов специальности
Автоматизация технологических процессов и производств
Профиль 01- Автоматизация технологических процессов и производств
(заочной формы обучения)
Одобрено редакционно-издательским советом
Института
Старый Оскол
Рецензент:
Составитель:
Симонова А.Г., Лазарева Т.И.
© Симонова А.Г., Лазарева Т.И.
© Кафедра АиПЭ
Лист для оценки работы студента
Ф.И.О. студента_____________________________________________
____________________________________________________________
Группа______________________________________________________
Ф.И.О. преподавателя_________________________________________
____________________________________________________________
Рецензия преподавателя:______________________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Общая оценка………………………….…………………………………
Подпись……………………..…..Дата «___»________________200__г.
Содержание
Домашнее задание № 1. 4
«Освоение математического пакета Mathcad». 4
Введение. 4
1.1 Цели и задачи домашнего задания. 4
1.2 Содержания домашнего задания. 5
1.3 Порядок выполнения домашнего задания. 15
1.4 Контрольные вопросы.. 26
Домашнее задание № 2. 27
«Основы работы в MatLab». 27
Введение. 27
2.1 Цели и задачи домашнего задания. 27
2.2 Содержания домашнего задания. 28
2.3. Порядок выполнения домашнего задания. 37
2.4 Контрольные вопросы.. 48
Список литературы.. 49
Введение
Рабочая тетрадь содержит необходимый теоретический материал, подробные инструкции по выполнению домашних работ на темы «Освоение математического пакета Mathcad» и «Основы работы в MatLab» по курсу «Компьютерное обеспечение специальности». Изучение этих программных пакетов будет способствовать более легкому и детальному усвоению последующих дисциплин, а также формированию практических навыков в работе с программными средствами, используемыми в дальнейшем для математических и научно-технических задач и оформления исследований.
Для успешного выполнения и защиты домашних заданий рекомендуется предварительно изучить теоретический материал, разобрать примеры приведенных задач. Домашние задания выполняются по разработанным по вариантам, оформляются в рабочих тетрадях. Перед защитой домашних заданий рабочие тетради сдаются на проверку преподавателю.
Домашнее задание № 1
«Освоение математического пакета Mathcad»
Введение
Mathcad является самым популярным из компьютерных математических пакетов компании МаthSoft. С его помощью можно решать самые разные математические задачи и оформлять результаты расчетов на высоком профессиональном уровне.
Mathcad позволяет записывать на экране компьютера формулы в их привычном виде. С его помощью можно решить почти любую математическую задачу символьно, либо численно. Текст можно размещать в любых местах вокруг уравнений, чтобы документировать процесс решения.
Mathcad имеет свою собственную справочную систему. Электронные книги делают доступными для использования в рабочем документе множество полезных формул, справочных данных и диаграмм простым нажатием кнопки. Интерфейс пакета обеспечивает слежение за ошибками: сообщение об ошибке отмечает формулу, в которой содержит ошибка; вырезку и вставку уравнений, текста и графики. Контекстная интерактивная система справок обеспечивает возможность получения помощи при выполнении любых операций.
Пакет Mathcad содержит встроенную систему единиц измерения и проверки размерности, встроенный алгоритм решения систем уравнений и неравенств, работает с комплексными числами, переменными и функциями, вычисляет производные, интегралы, суммы рядов и т.д.
Mathcad содержит большой набор статистических функций, включая линейную регрессию, гамма - функцию, интеграл ошибок, функции вероятностных распределений, позволяет работать с векторами и матрицами, включая операции матричного умножения, обращения матриц, транспонирования, вычисления определителя матриц, скалярное и векторное умножение и т.д.
1.1 Цели и задачи домашнего задания
Знакомство с пакетом Mathcad, принципами его работы, приобретение навыков работы по вводу, редактированию формул, проведению вычислений с применением встроенных функций, созданию и изменению графиков.
1.2 Содержания домашнего задания
Вариант задания каждого студента соответствует его порядковому номеру по списку в журнале.
Описать порядок действий (команд), произведенных при решении каждого задания.
Задание 1.2.1
Упростить:
1. 
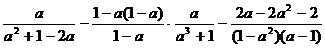
2. 
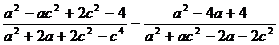
3. 
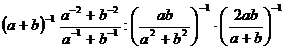
4. 
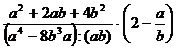
5. 
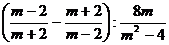
6. 
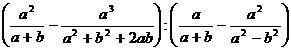
7. 
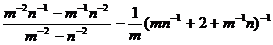
8. 
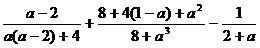
9. 
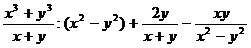
10. 
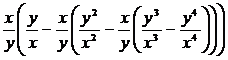
11. 
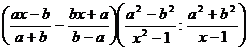
12. 
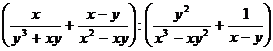
13. 
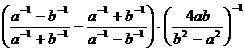
14. 
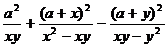
15. 
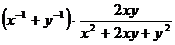
16. 
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
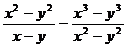
Задание 1.2.2
Разложить выражение:
1. 
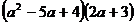
2. 
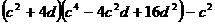
3. 
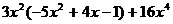
4. 
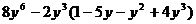
5. 
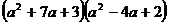
6. 
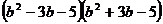
7. 
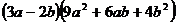
8. 
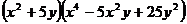
9. 
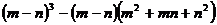
10. 
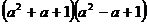
11. 
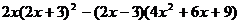
12. 
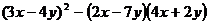
13. 
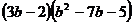
14. 
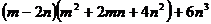
15. 
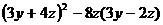
16. 
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
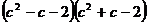
Задание 1.2.3
Разложить на множители:
1. 
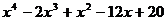
2. 
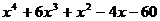
3. 
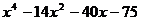
4. 
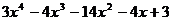
5. 
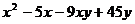
6. 
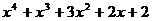
7. 
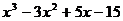
8. 
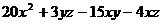
9. 
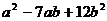
10. 
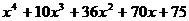
11. 
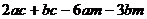
12. 
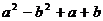
13. 
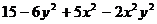
14. 
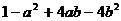
15. 
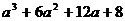
16. 
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
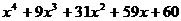
Задание 1.2.4
Разложить на простейшие дроби рациональную дробь:
1. 
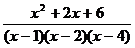
2. 
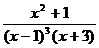
3. 
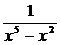
4. 
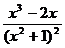
5. 
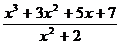
6. 
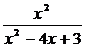
7. 
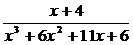
8. 
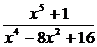
9. 
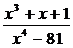
10. 
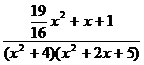
11. 
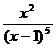
12. 
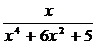
13. 
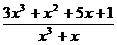
14. 
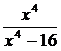
15. 
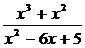
16. 
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
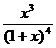
Задание 1.2.5
Найти:
1. 
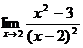
2. 
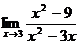
3. 
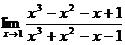
4. 
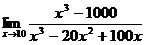
5. 
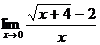
6. 
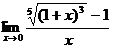
7. 
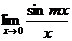
8. 
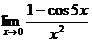
9. 
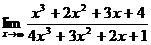
10. 
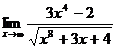
11. 
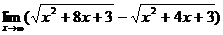
12. 
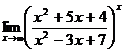
13. 
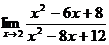
14. 
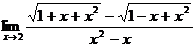
15. 
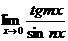
16. 
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
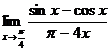
Задание 1.2.6
Найти производные функций:
1. 
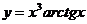
2. 
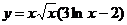
3. 
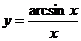
4. 
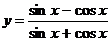
5. 
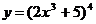
6. 
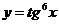
7. 
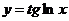
8. 
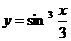
9. 
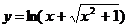
10. 
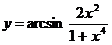
11. 
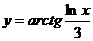
12. 
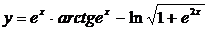
13. 
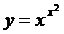
14. 
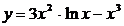
15. 
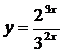
16. 
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
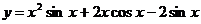
Задание 1.2.7
Найти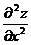 
, 
, 
:
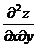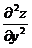1. 
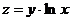
2. 
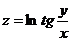
3. 
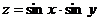
4. 
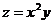
5. 
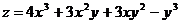
6. 
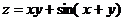
7. 
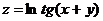
8. 
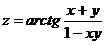
9. 
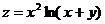
10. 
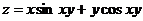
11. 
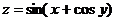
12. 
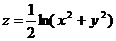
13. 
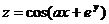
14. 
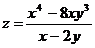
15. 
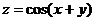
16. 
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
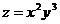
Задание 1.2.8
Найти интеграл:
1. 
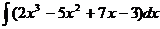
2. 
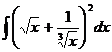
3. 
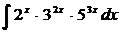
4. 
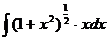
5. 
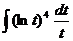
6. 
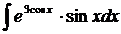
7. 
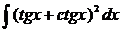
8. 
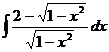
9. 
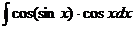
10. 
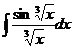
11. 
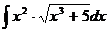
12. 
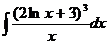
13. 
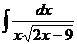
14. 
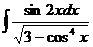
15. 
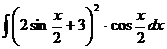
16. 
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
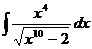
Задание 1.2.9
Вычислить интеграл:
1. 
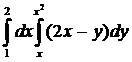
2. 
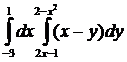
3. 
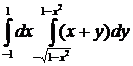
4. 
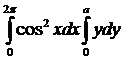
5. 
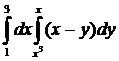
6. 
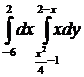
7. 
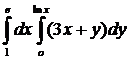
8. 
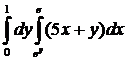
9. 
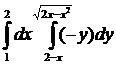
10. 
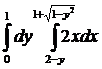
11. 
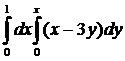
12. 
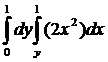
13. 
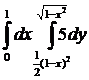
14. 
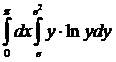
15. 
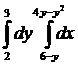
16. 
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
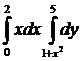
Задание 1.2.10
Решите уравнение:
1. 
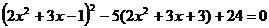
2. 
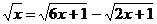
3. 
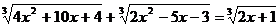
4. 
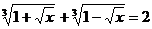
5. 
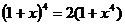
6. 
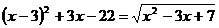
7. 
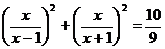
8. 
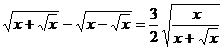
9. 
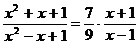
10. 
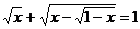
11. 
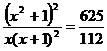
12. 
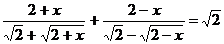
13. 
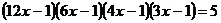
14. 
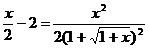
15. 
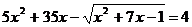
16. 
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
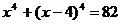
Задание 1.2.11
Решите систему уравнений, используя функцию Find:
1. 
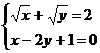
2. 
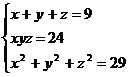
3. 
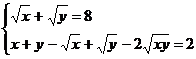
4. 
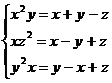
5. 
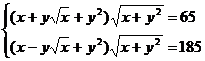
6. 
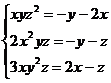
7. 
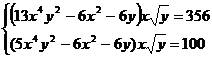
8. 
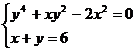
9. 
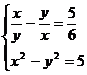
10. 
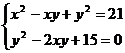
11. 
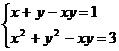
12. 
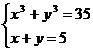
13. 
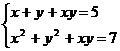
14. 
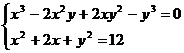
15. 
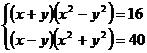
16. 
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
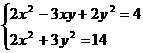
Задание 1.2.12
Решите систему уравнений:
a. матричным способом и используя функцию lsolve;
b. методом Гаусса:
1. 
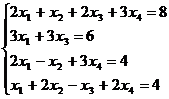
2. 
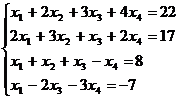
3. 
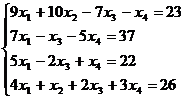
4. 
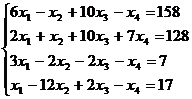
5. 
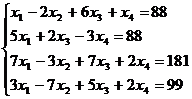
6. 
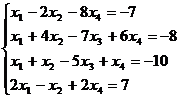
7. 
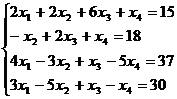
8. 
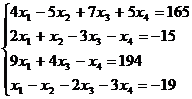
9. 
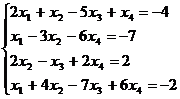
10. 
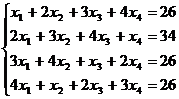
11. 
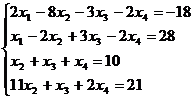
12. 
13. 
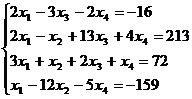
14. 
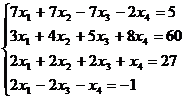
15. 
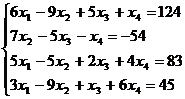
16. 
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
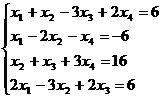
Задание 1.2.13
Построить график функции:
1. 
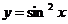
2. 
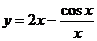
3. 
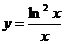
4. 
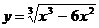
5. 
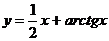
6. 
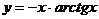
7. 
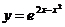
8. 
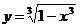
9. 
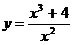
10. 
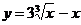
11. 
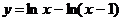
12. 
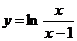
13. 
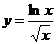
14.
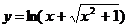
15. 
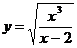
16. 
______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
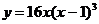
1.3 Порядок выполнения домашнего задания
Знакомство с Mathcad
Двойной щелчок на пиктограмме Mathcad вызывает появление заставки. Затем открывается окно приложения. Оно имеет ту же структуру, что и большинство приложений Windows. Сверху вниз располагаются:
- заголовок окна;
- строка меню;
- панели инструментов Standard (стандартная), Formatting (форматирования), Resources (ресурсы);
- рабочая область;
- строка состояния.
Команды выполняются как с помощью меню, так и панелей инструментов или клавиатуры.
Строка меню содержит девять заголовков, щелчок мыши на каждом из которых приводит к появлению соответствующего меню с перечнем команд:
· File(Файл)–команды, связанные с созданием, открытием, сохранением, пересылкой по электронной почте и распечаткой на принтере файлов с документами;
· Edit (Правка) –команды, относящиеся к правке текста (копирование, вставка, удаление и т.п.);
· View (Вид) –команды, управляющие внешним видом документа в окне редактора Mathcad, а также команды, создающие файлы анимации;
· Insert (Вставка) – команды вставки различных объектов в докуметы;
· Format (Формат) –команды форматирования текста, формул и графиков;
· Tools (Инструменты) –команды управления вычислительным процессом и дополнительными возможностями;
· Symbolisc (Символика) –команды символьных вычислений;
· Window (Окно) –команды управления расположением окон с различными документами на экране;
· 
Help (Справка)–команды вызова справочной информации, сведений о версии программы.
Mathcad снабжен дополнительными средствами для ввода и редактирования математических символов, одним из которых является панель инструментов Math (рис.1). Она содержит инструменты для вставки в документы математических объектов (операторов, графиков, элементов программ и т.п.). Панель содержит девять кнопок, нажатие каждой из которых приводит к появлению на экране еще одной панели инструментов:
§ Calculator– служит для вставки основных математических операций;
§ Graph (График) – для вставки графиков;
§ Matrix (Матрица) – для вставки матриц и матричных операторов;
§ Evaluation (Выражения) – для вставки операторов управления вычислениями;
§ Calculus (Вычисления) – для вставки операторов интегрирования, дифференцирования, суммирования;
§ Boolean (Булевы операторы) – для вставки логических (булевых) операторов;
§ Programming (Программирование) – для программирования средствами Mathcad;
§ Greek (Греческие символы) – для вставки греческих символов;
§ Symbolic – для вставки символьных операторов.
Определение переменных
Для определения переменной, достаточно ввести ее имя и присвоить некоторое значение, для чего служит оператор присваивания, который вводится с помощью клавиши <:> или нажатием соответствующей кнопки Definition (Присваивание) на панели инструментов Calculator или Evaluation (Выражения). Затем, в появившийся местозапонитель, ввести новое значение переменной.
Рис.3.
Символьные вычисления
Символьные вычисления в Mathcad можно осуществлять в двух различных вариантах:
· с помощью команд меню;
· с помощью оператора символьного вывода ®, ключевых слов символьного процессора и обычных формул.
Упрощение выражений
Упрощение выражений – наиболее часто применяемая операция. При упрощении используются различные арифметические формулы, приведение подобных слагаемых, тригонометрические тождества, пересчет обратных функций и др.
Чтобы упростить выражение с помощью меню:
1. Введите выражение.
2. Выделите выражение целиком или его часть, которую нужно упростить.
3. Выберите команду Symbolics/Simplify (Символика/Упростить).
Для упрощения выражения при помощи оператора символьного вывода используется ключевое слово simplify.
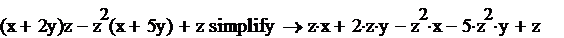
1.3.4.2 Разложений выражений
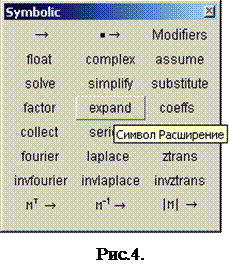
Операция символьного разложения, или расширения, выражений противоположна по смыслу операции упрощения. В ходе разложения раскрываются все суммы и произведения, а сложные тригонометрические зависимости разлагаются с помощью тригонометрических тождеств. Разложение выражений производится путем выбора команды Symbolics/Expand (Символика/Разложить) либо использованием вместе с оператором символьного вывода ключевого слова expand, для этого необходимо:
1. Ввести выражение, например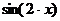 
.
2. Нажать кнопку Expand (Разложить) на панели Symbolic (рис. 4.).
3. Введите в местозаполнитель после появившегося слова expand имя переменной х либо нажмите клавишу <Del>, чтобы просто удалить местозаполнитель.
4. Нажмите клавишу <Enter> либо просто щелкните мышью за пределами выражения.
Разложение на множители
Разложение выражений на простые множители производится при помощи команды Symbolics/Factor (Символика/Разложить на множители) либо использованием вместе с оператором символьного вывода ключевого слова factor. Эта операция позволяет разложить полиномы на произведение более простых полиномов, а целые числа на простые сомножители.
Интегрирование
Интегрирование в Mathcad реализовано в виде вычислительного оператора. Для вычисления неопределенного интеграла от некоторого выражения по определенной переменной выделите в выражении переменную и выполните команду Symbolics/Variable/Integrate (Символика/Переменная/Интегрировать). Вычисленное аналитическое представление неопределенного интеграла появиться ниже.
Чтобы вычислить определенный интеграл, следует напечатать его обычную математическую форму в документе. Делается это с помощью панели Calculus (Вычисления) нажатием кнопки со значком интеграла или вводом с клавиатуры сочетания клавиш <Shift>+<7>. Появится символ интеграла с несколькими местозаполнителями (рис.6), в которые нужно ввести нижний и верхний интервалы интегрирования, подынтегральную функцию и переменную интегрирования. Чтобы получить результат интегрирования, следует ввести знак равенства (=) или символьного равенства (®).
 |
Дифференцирование
С помощью Mathcad можно вычислять производные скалярных функций любого количества аргументов, от 0-го до 5-го порядка включительно. И функции, и аргументы могут быть как действительными, так и комплексными.
Для того чтобы продифференцировать функцию f(x) необходимо:
1. 
Ввести оператор дифференцирования нажатием кнопки Derivative (Производная) на панели Calculus (Вычисления) или введите с клавиатуры вопросительный знак <?>,
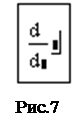
2. В появившихся местозаполнителях (рис.7) ввести функцию f(x) и имя самого аргумента x.
3. Ввести оператор (®) символьного вывода для получении ответа.
Чтобы вычислить производную n-го порядка, нужно проделать те же самые действия, что и при взятии первой производной, за тем исключением, что вместо оператора первой производной необходимо применить оператор n-й производной – NthDerivative на панели Calculus (Вычисления) или нажать сочетание клавиш <Ctrl>+<?>.
 |
Решение уравнений
Рассмотрим алгебраическое уравнение f(x)=0. Данное уравнение можно решить двумя способами:
I. способ:
1. Ввести выражение f(x);
2. Выделить переменную, относительно которой будет решаться уравнение, приравнивающее выражение к нулю - х;
3. Выбрать в меню Symbolics (Символика) пункт Variable / Solve (Переменная/Решить).
II. способ:
Щелкните по кнопке решения уравнений solve в панели символьных вычислений Symbolic. Введите в местозаполнитель слева от ключевого словаsolve (решить) выражение для правой части уравнения, а в позиции справа отsolve (решить) — имя переменной, относительно которой нужно решить уравнение, и щелкните по свободному месту в рабочем документе. Результат — значение корня уравнения — будет отображен в рабочем документе справа от стрелки
Массивы
Массивами - называют упорядоченные последовательности чисел. Существует несколько способов создания массива. Самый простой и наглядный способ создания заключается в следующем:
1. Нажать кнопку Matrix or Vector (Матрица или вектор) на панели Matrix (Матрица) либо клавиши <Ctrl> + <M>, либо выбрать пункт меню
Insert / Matrix (Вставка / Матрица);
2. В диалоговом окне Insert Matrix (Вставка матрицы) задать целое число столбцов и строк матрицы;
3. Нажать кнопку ОК или Insert (Вставить) – в результате в документ будет вставлена заготовка матрицы с определенным числом строк и столбцов;
4. Ввести значения в местозаполнители элементов матрицы. Переходить от одного элемента матрицы к другому можно с помощью указателя мыши либо клавиш со стрелками.
Транспонирование
Транспонированием называют операцию, переводящую матрицу размерности N´M в матрицу размерности M´N, делая столбы исходной матрицы строками, а строки – столбцами.
Ввод символа транспонирования осуществляется с помощью панели инструментов Matrix (Матрица) или нажатием клавиш <Ctrl>+<1> (для вставки символа транспонирования матрица должна находится между линиями ввода).
Сложение
В Mathcad можно как складывать матрицы, так и вычитать их друг из друга. Для этих операторов применяются символы <+> и <->, соответственно. Матрицы должны иметь одинаковую размерность, иначе будет выдано сообщение об ошибке. Каждый элемент суммы двух матриц равен сумме соответствующих элементов матриц-слагаемых.
Кроме сложения матриц, Mathcad поддерживает операцию сложения матрицы со скаляром. Каждый элемент результирующей матрицы равен сумме соответствующего элемента исходной матрицы и скалярной величины.
Умножение
При умножении надо помнить, что матрицу размерностью M´N допустимо умножать только на матрицу размерности N´P (P может быть любым). В результате получается матрица размерностью M´P.
Чтобы ввести символ умножения, нужно нажать клавишу со звездочкой <*>. Аналогично производится умножение матриц на скалярную величину.
Обратная матрица
Поиск обратной матрицы возможен, если матрица квадратная и ее определитель не равен нулю. Произведение исходной матрицы на обратную по определению является единичной матрицей. Для ввода оператора поиска обратной матрицы нажмите кнопку Inverse (Обратная матрица) на панели инструментов Matrix (Матрица).
Решение матричных уравнений
Рассмотрим систему n линейных алгебраических уравнений относительно n неизвестных x1, x2,…,xn.
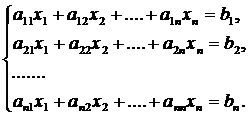(1)
В соответствии с правилом умножения матриц рассмотренная система линейных уравнений может быть записана в виде: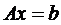 
, где:
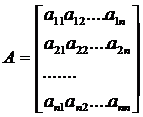
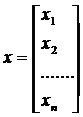
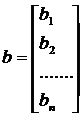
Если определитель матрицы А не равен 0, то система имеет единственное решение, т.к. существует обратная матрица А-1 при умножении обеих частей уравнения на которую получаем:
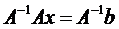
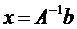
Системы линейных уравнений удобно решать с помощью функции lsolve:
lsolve(А, b)-возвращается вектор решения x такой, что 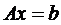(см. рис. 9).
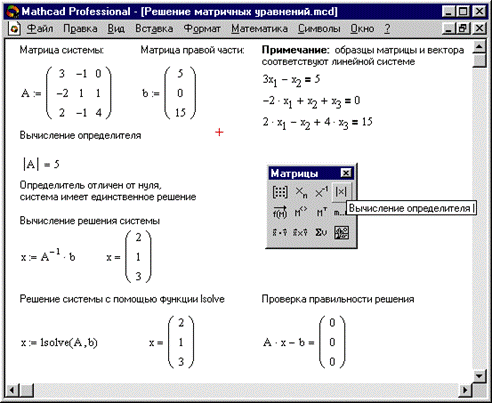
Рис.9.
Метод Гаусса
Метод Гаусса состоит в том, что систему (1) приводят последовательным исключение неизвестных к эквивалентной системе с треугольной матрицей:
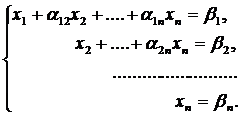
решение которой находят по рекуррентным формулам:
, 
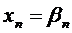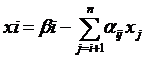
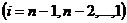
В матричной записи это означает, что сначала (прямой ход метода Гаусса) элементарными операциями над строками приводят расширенную матрицу системы к ступенчатому виду:
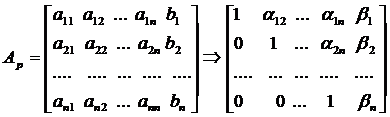
а затем (обратный ход метода Гаусса) эту ступенчатую матрицу преобразуют так, чтобы в первых n столбцах получилась единичная матрица:
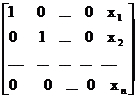
Последний, (n+1) этой матрицы содержит решение системы (1).
В Mathcad прямой и обратный ходы метода Гаусса выполняет функция rref(A). На рис.10 показано решение системы линейных уравнений методом Гаусса, в котором используются следующие показано решение системы линейных уравнений мето