Методы первого порядка безусловной многомерной минимизации (градиентные методы). Метод Гаусса-Зейделя
Задание:
Создать приложение для нахождения минимума функции f(x,у) методом Гаусса-Зейделя. Определить сколько итераций потребуется для достижения точности l=10-3, 10-5 , 10-7 при одних и тех же начальных приближениях.
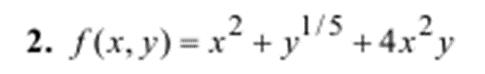
Кодпрограммы:
#include "stdafx.h"
#include <conio.h>
#include <math.h>
#include <stdlib.h>
#include <windows.h>
#include <locale.h>
using namespace std;
#define N 2
int i;
float f(float x[N+1]);
void graddirection(void);
void scanforonedim(void);
void pausa();
void outputresult(void);
float absgrad,e1,h,h1,z,s[3],x[3];
float K = 2;
float f(float x[N+1])
{
float y;
y = x[1]*x[1]+4*x[1]*x[1]*x[2]+pow(x[2],1/5);
return y;
}
void graddirection(void)
{
float gradx,grady;
gradx =2*x[1]+8*x[1]*x[2];
grady = 4*x[1]*x[1]+0.2/x[2];
absgrad = sqrt(gradx*gradx+grady*grady);
if(absgrad!=0)
{
s[1] = gradx/absgrad;
s[2]=grady/absgrad;
};
}
void scanforonedim(void)
{
short a;
float d1,z1;
z=f(x);
graddirection();
do{
d1=fabs(h1);
for(i = 1; i<=N; i++) x[i]=h1*s[i];
z1=f(x); a = (z1<z);
if(!a) h1 /= -K;
z=z1;
}
while (a || d1 >=e1);
}
void pausa()
{
printf("\nНажимите любую кнопку для продолжения...\n");
_getch();
};
void outputresult(void)
{
printf("Вектор приближения (x1,x2) на данном шаге ");
printf("вычислений ");
printf("x1=%f x2=%f\n",x[1],x[2]);
printf("f(x1,x2) = %f\n", f(x));
pausa();
};
void main()
{
setlocale(LC_ALL,"Rus");
float d,e;
char finish;
printf("Введите координаты начального ");
printf("вектора (x1,x2)\n");
for(i = 1;i<=N;i++) scanf_s("%f",&x[i]);
graddirection();
if(!absgrad)
{
printf("Стационарнаяточка x1 = %f", x[1]);
printf("x2=%f",x[2]);
};
e = 0.0001;
outputresult();
h=0.2;
e1=e/K;
do{
d=fabs(h);
h1=h;
scanforonedim();
outputresult();
h /=K;
}while(d>=e);
pausa();
}
Результат:
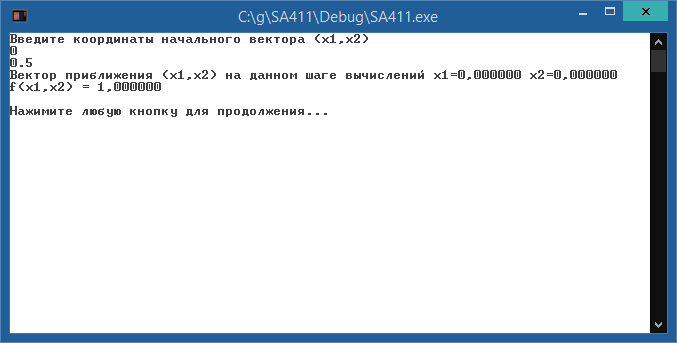
Лабораторная работа № 5
Решение задач линейного программирования с помощью ПОИСКА РЕШЕНИЙ в среде EXCEL
Цель работы:
1) Научиться составлять математические модели линейных задач.
2) Ознакомиться с технологией решения задач линейного программирования с помощью ПОИСКА РЕШЕНИЙ в среде EXCEL.
Задание:
Решить задачи, используя надстройку Excel Поиск решений
Три типа самолетов следует распределить между двумя авиалиниями. В таблице заданы количество самолетов каждого типа, месячный объём перевозок каждым самолетом на каждой авиалинии и соответствующие эксплутационные расходы. Требуется распределить самолёты по авиалиниям так, чтобы при минимальных суммарных эксплуатационных расходах перевезти по каждой из них соответственно не менее 300 и 200 ед. груза.
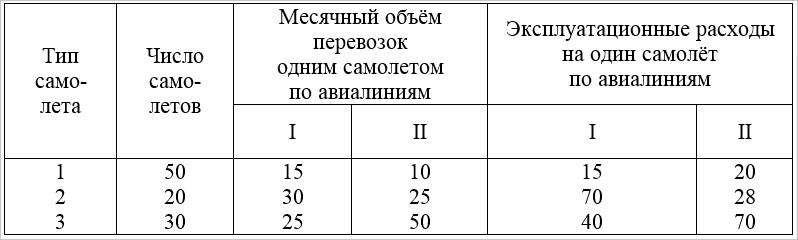
Математическая модель задачи:
x1 ,x2, x3 – количество самолётов, необходимых для перелёта
(x1*15) + (x2*30) + (x3*25) ≥ 300
(50-x1)*10 + (20-x2)*25 + (30-x3)*50 ≥ 200
(x1*15) +(x2*70) + (x3*40) + (50-x1)*20 + (20-x2)*28 + (30-x3)*70 -> min
xj≥ 0
Результаты решения задач с помощью ПОИСКА РЕШЕНИЙ в среде EXCEL

Выводы по работе
В ходе выполнения работы была составлена математическая модель задачи; получено решение через сервис поиск решения. По результатам проверки был сделан вывод о том, что сервис правильно подобрал решение.
Лабораторная работа № 6.
Векторная оптимизация (метод линейной комбинации частных критериев, метод ведущего критерия, метод последовательных уступок, метод равных и наименьших отклонений).
Цель работы:
1) ознакомиться с теорией векторной оптимизации;
