Решение хорошо структурированных задач. Методы оптимизации. Алгоритм Свена. Метод золотого сечения.
Отчеты
по лабораторным работам
по дисциплине «Системный анализ»
Вариант №2
Выполнил: студент гр. АСОИР-131
Галимский И.А.
Проверил: преподаватель
Сергеенко О.В.
Могилев, 2014
Лабораторная работа №2
Решение хорошо структурированных задач. Методы оптимизации. Алгоритм Свена. Метод золотого сечения.
Задание:
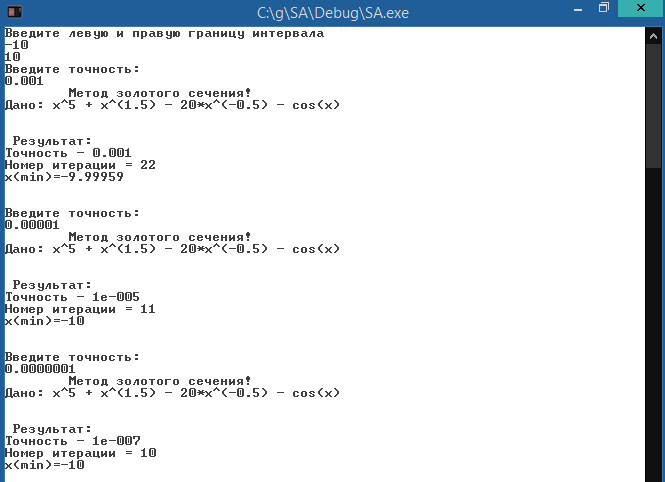
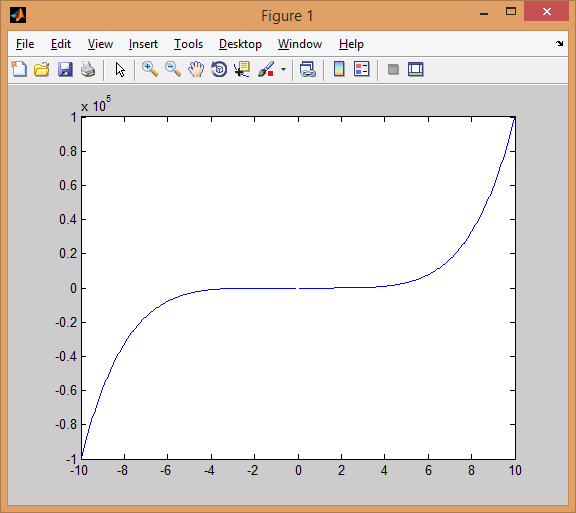
Создать приложение для нахождения минимума функции f(x) методом золотого сечения. Определить сколько итераций потребуется для достижения точности l=10-3, 10-5, 10-7 при одних и тех же начальных приближениях.
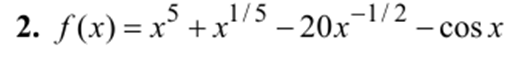
Кодпрограммы:
#include "stdafx.h"
#include <iostream>
#include <math.h>
#include <conio.h>
using namespace std;
double function(double x)
{
return (((pow(x,5) + pow(x,0.2)) - 20*pow(x,(-0.5)) - cos(x)));//вашафункция
}
void main()
{
setlocale(LC_ALL, "Russian");
double eps;
double left,right=0;//границы интервала на котором надо найти минимумы
cout<<"Введите левую и правую границу интервала"<<endl;
cin>>left>>right;
for(int i = 0; i < 3; i++)
{
cout<<"Введите точность: "<<endl;
cin>>eps;
int count=1;//номеритерации
static double a=left,b=right;
static double x1,x2;
x1=a+0.382*(b-a);
x2=a+0.618*(b-a);
static double min;//окончательныйрезультат
static double y1, y2;
y1=function(x1);
y2=function(x2);
cout<<"\tМетод золотого сечения!"<<endl;
cout<<"Дано: x^5 + x^(1.5) - 20*x^(-0.5) - cos(x)\n"<<endl;
while((b-a)>eps)
{
if(y1>=y2)
{
a=x1;
b=b;
x1=x2;
y1=function(x1);
x2=a+0.618*(b-a);
y2=function(x2);
}
else
{
a=a;
b=x2;
x2=x1;
y2=function(x2);
x1=a+0.382*(b-a);
y1=function(x1);
}
count++;
min=(a+b)/2;
}
cout<<"\n Результат: \n";
cout<<"Точность - "<<eps<<endl;
cout<<"Номеритерации = "<<count<<endl;
cout<<"x(min)="<<min<<endl<<endl<<endl;
};
system("pause");
}
Результат:
Лабораторная работа 3.
Методы нулевого порядка безусловной многомерной оптимизации. Метод сопряженных направлений (метод Пауэлла).
Задание:
Задание. Создать приложение для нахождения минимума функции f(x) методом Пауэлла. Определить сколько итераций потребуется для достижения точности l=10-3, 10-5 , 10-7 при одних и тех же начальных приближениях.
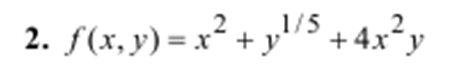
Кодпрограммы:
#include "stdafx.h"
#include <iostream>
#include <math.h>
#include <conio.h>
using namespace std;
double f(double x1,double x2) {
return (pow(x1,2)+pow(x1,2)*x2*4+pow(x2,0.2));
}
int main(){
double E=0, min, var[200], t;
cout<<"Enter E"<<endl;
cin>>E;
int i, j, n=2, k=0;
int s=0, I[100];
int iter = 0;
double d[3][3]={{0,1}, {1,0}, {0,1}};
double X[20][20], Y[20][40], Xz[1][2];
I[s]=0;
cout <<" Enter X0:"<<endl; //задаем начальную точку Хо
for(i=0;i<1;i++)
for(int j=0;j<2;j++)
cin >>X[i][j]; cout <<"X("<<X[0][0]<<";"<<X[0][1]<<")\n";
for(i=0;i<1;i++) //Y0 = Xo
for(j=0;j<2;j++)
Y[i][j]=X[i][j]; cout <<"Y("<<Y[0][0]<<";"<<Y[0][1]<<")\n";
//.2.........................
TWO: cout <<" __2__"<<endl;
min=f(Y[I[s]][0],Y[I[s]][1]);
i=0;
iter++;
for(t=-50;t<50;t++,i++) //вывод различных значений ф-ции
{
var[i]=f( Y[I[s]][0]+t*d[I[s]][0], Y[I[s]][1]+t*d[I[s]][1]);
cout <<"var ["<<i<<"] = "<<var[i]<<endl;
}
for(i=0;i<100;i++) //вывод наименьшего значения ф-ции
if(var[i] < min)
min = var[i];
cout <<"min var[] = "<<min<<endl;
for(int index=0;index<100;index++) //вывод t
{
if( min==var[index] )
t=index-50;
}
cout <<"T = "<<t<<endl;
Y[I[s]+1][0] = Y[I[s]][0] + t*d[I[s]][0];
Y[I[s]+1][1] = Y[I[s]][1] + t*d[I[s]][1];
cout <<"Y["<<I[s]+1<<"] = ("<<Y[I[s]+1][0]<<";";
cout <<Y[I[s]+1][1]<<")"<<endl;
//.3.................
THREE: cout <<" __3__"<<endl;
if(I[s] < n-1)
{
cout <<"I[s] < n-1"<<endl;
I[s]=I[s]+1;
cout <<"I[s] = "<<I[s]<<endl;
goto TWO;
} //*/
if(I[s] == n-1)
{
cout <<"I[s] == n-1"<<endl;
if( (Y[n][0]==Y[0][0]) && (Y[n][1]==Y[0][1]) ){
Xz[0][0]=Y[n][0]; cout <<"Xz("<<Xz[0][0]<<";";
Xz[0][1]=Y[n][1]; cout <<Xz[0][1]<<")"<<endl;
}
else {
cout <<"Yn != Y0 "<<endl;
I[s]=I[s]+1;
cout <<"I[s] = "<<I[s]<<endl;
goto TWO; }
}
if(I[s] == n)
{
cout <<"I[s] == n"<<endl;
if( (Y[n+1][0]==Y[1][0]) && (Y[n+1][1]==Y[1][1]) ){
Xz[0][0]=Y[n+1][0]; cout <<"Xz("<<Xz[0][0]<<";";
Xz[0][1]=Y[n+1][1]; cout <<Xz[0][1]<<")"<<endl;
}
if( (Y[n+1][0]!=Y[1][0]) || (Y[n+1][1]!=Y[1][1]) ){
goto Fourth;
}
}
//.4.........................
Fourth: cout <<" __4__"<<endl;
X[k+1][0]=Y[n+1][0]; cout <<"X["<<(k+1)<<"] = ("<<X[k+1][0];
X[k+1][1]=Y[n+1][1]; cout <<";"<<X[k+1][1]<<")"<<endl;
//...........a...............
if( pow( ( pow((X[k+1][0]-X[k][0]),2)+pow((X[k+1][1]-X[k][1]),2) ),1/2.0)<E ){
cout <<"X(k+1) - X(k) = "<<pow( ( pow((X[k+1][0]-X[k+1][0]),2)+
pow((X[k+1][1]-X[k+1][1]),2) ),1/2.0);
Xz[0][0]=X[k+1][0];
Xz[0][1]=X[k+1][1];
}
//..................b.....................
if( pow( ( pow((X[k+1][0]-X[k][0]),2)+pow((X[k+1][1]-X[k][1]),2) ),1/2.0)>E ){
d[0][0]=d[n][0]=Y[n+1][0]-Y[1][0]; cout <<"d0 = ("<<d[0][0];
d[0][1]=d[n][1]=Y[n+1][1]-Y[1][1]; cout <<";"<<d[0][1]<<")"<<endl;
d[I[s]][0]=d[I[s]+1][0];
d[I[s]][1]=d[I[s]+1][1];
if( (d[1][0]*d[2][1]-d[1][1]*d[2][0]) != 0){
cout <<"rang(D1,...,Dn) = n"<<endl;
Y[0][0]=X[k+1][0]; cout <<"Y0 = ("<<Y[0][0]<<";";
Y[0][1]=X[k+1][1]; cout <<Y[0][1]<<")\n";
k=k+1;
I[s]=0;
goto TWO; }
if( (d[1][0]*d[2][1]-d[1][1]*d[2][0]) == n){
cout <<"rang(D1,...,Dn) < n"<<endl;
Y[0][0]=X[k+1][0];
Y[0][1]=X[k+1][1];
k=k+1; I[s]=0;
goto TWO;
}
}
cout<<endl<<endl<<"Iter - "<<iter<<endl;
cout<<endl<<endl<<endl<<endl<<endl;
cout<<"ANSWER"<<endl;
cout <<"\nXz("<<Xz[0][0]<<";"<<Xz[0][1]<<")"<<endl;
getch();
}
Результат:
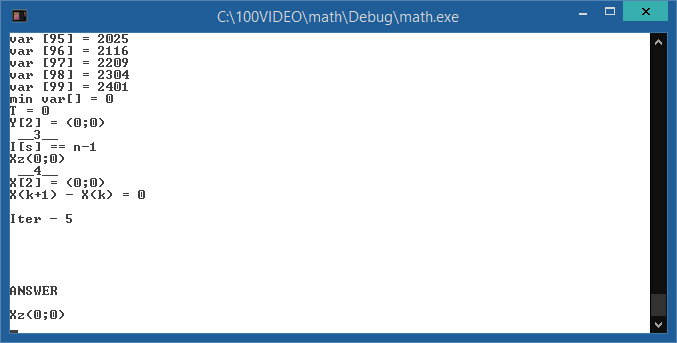
Лабораторная работа № 4.
Лабораторная работа № 5
Выводы по работе
В ходе выполнения работы была составлена математическая модель задачи; получено решение через сервис поиск решения. По результатам проверки был сделан вывод о том, что сервис правильно подобрал решение.
Лабораторная работа № 6.
Отчеты
по лабораторным работам
по дисциплине «Системный анализ»
Вариант №2
Выполнил: студент гр. АСОИР-131
Галимский И.А.
Проверил: преподаватель
Сергеенко О.В.
Могилев, 2014
Лабораторная работа №2
Решение хорошо структурированных задач. Методы оптимизации. Алгоритм Свена. Метод золотого сечения.
Задание:
Создать приложение для нахождения минимума функции f(x) методом золотого сечения. Определить сколько итераций потребуется для достижения точности l=10-3, 10-5, 10-7 при одних и тех же начальных приближениях.
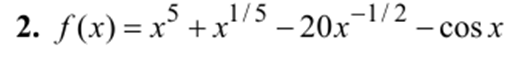
Кодпрограммы:
#include "stdafx.h"
#include <iostream>
#include <math.h>
#include <conio.h>
using namespace std;
double function(double x)
{
return (((pow(x,5) + pow(x,0.2)) - 20*pow(x,(-0.5)) - cos(x)));//вашафункция
}
void main()
{
setlocale(LC_ALL, "Russian");
double eps;
double left,right=0;//границы интервала на котором надо найти минимумы
cout<<"Введите левую и правую границу интервала"<<endl;
cin>>left>>right;
for(int i = 0; i < 3; i++)
{
cout<<"Введите точность: "<<endl;
cin>>eps;
int count=1;//номеритерации
static double a=left,b=right;
static double x1,x2;
x1=a+0.382*(b-a);
x2=a+0.618*(b-a);
static double min;//окончательныйрезультат
static double y1, y2;
y1=function(x1);
y2=function(x2);
cout<<"\tМетод золотого сечения!"<<endl;
cout<<"Дано: x^5 + x^(1.5) - 20*x^(-0.5) - cos(x)\n"<<endl;
while((b-a)>eps)
{
if(y1>=y2)
{
a=x1;
b=b;
x1=x2;
y1=function(x1);
x2=a+0.618*(b-a);
y2=function(x2);
}
else
{
a=a;
b=x2;
x2=x1;
y2=function(x2);
x1=a+0.382*(b-a);
y1=function(x1);
}
count++;
min=(a+b)/2;
}
cout<<"\n Результат: \n";
cout<<"Точность - "<<eps<<endl;
cout<<"Номеритерации = "<<count<<endl;
cout<<"x(min)="<<min<<endl<<endl<<endl;
};
system("pause");
}
Результат:


Лабораторная работа 3.
Методы нулевого порядка безусловной многомерной оптимизации. Метод сопряженных направлений (метод Пауэлла).
Задание:
Задание. Создать приложение для нахождения минимума функции f(x) методом Пауэлла. Определить сколько итераций потребуется для достижения точности l=10-3, 10-5 , 10-7 при одних и тех же начальных приближениях.
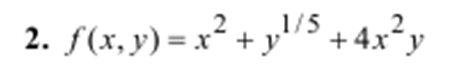
Кодпрограммы:
#include "stdafx.h"
#include <iostream>
#include <math.h>
#include <conio.h>
using namespace std;
double f(double x1,double x2) {
return (pow(x1,2)+pow(x1,2)*x2*4+pow(x2,0.2));
}
int main(){
double E=0, min, var[200], t;
cout<<"Enter E"<<endl;
cin>>E;
int i, j, n=2, k=0;
int s=0, I[100];
int iter = 0;
double d[3][3]={{0,1}, {1,0}, {0,1}};
double X[20][20], Y[20][40], Xz[1][2];
I[s]=0;
cout <<" Enter X0:"<<endl; //задаем начальную точку Хо
for(i=0;i<1;i++)
for(int j=0;j<2;j++)
cin >>X[i][j]; cout <<"X("<<X[0][0]<<";"<<X[0][1]<<")\n";
for(i=0;i<1;i++) //Y0 = Xo
for(j=0;j<2;j++)
Y[i][j]=X[i][j]; cout <<"Y("<<Y[0][0]<<";"<<Y[0][1]<<")\n";
//.2.........................
TWO: cout <<" __2__"<<endl;
min=f(Y[I[s]][0],Y[I[s]][1]);
i=0;
iter++;
for(t=-50;t<50;t++,i++) //вывод различных значений ф-ции
{
var[i]=f( Y[I[s]][0]+t*d[I[s]][0], Y[I[s]][1]+t*d[I[s]][1]);
cout <<"var ["<<i<<"] = "<<var[i]<<endl;
}
for(i=0;i<100;i++) //вывод наименьшего значения ф-ции
if(var[i] < min)
min = var[i];
cout <<"min var[] = "<<min<<endl;
for(int index=0;index<100;index++) //вывод t
{
if( min==var[index] )
t=index-50;
}
cout <<"T = "<<t<<endl;
Y[I[s]+1][0] = Y[I[s]][0] + t*d[I[s]][0];
Y[I[s]+1][1] = Y[I[s]][1] + t*d[I[s]][1];
cout <<"Y["<<I[s]+1<<"] = ("<<Y[I[s]+1][0]<<";";
cout <<Y[I[s]+1][1]<<")"<<endl;
//.3.................
THREE: cout <<" __3__"<<endl;
if(I[s] < n-1)
{
cout <<"I[s] < n-1"<<endl;
I[s]=I[s]+1;
cout <<"I[s] = "<<I[s]<<endl;
goto TWO;
} //*/
if(I[s] == n-1)
{
cout <<"I[s] == n-1"<<endl;
if( (Y[n][0]==Y[0][0]) && (Y[n][1]==Y[0][1]) ){
Xz[0][0]=Y[n][0]; cout <<"Xz("<<Xz[0][0]<<";";
Xz[0][1]=Y[n][1]; cout <<Xz[0][1]<<")"<<endl;
}
else {
cout <<"Yn != Y0 "<<endl;
I[s]=I[s]+1;
cout <<"I[s] = "<<I[s]<<endl;
goto TWO; }
}
if(I[s] == n)
{
cout <<"I[s] == n"<<endl;
if( (Y[n+1][0]==Y[1][0]) && (Y[n+1][1]==Y[1][1]) ){
Xz[0][0]=Y[n+1][0]; cout <<"Xz("<<Xz[0][0]<<";";
Xz[0][1]=Y[n+1][1]; cout <<Xz[0][1]<<")"<<endl;
}
if( (Y[n+1][0]!=Y[1][0]) || (Y[n+1][1]!=Y[1][1]) ){
goto Fourth;
}
}
//.4.........................
Fourth: cout <<" __4__"<<endl;
X[k+1][0]=Y[n+1][0]; cout <<"X["<<(k+1)<<"] = ("<<X[k+1][0];
X[k+1][1]=Y[n+1][1]; cout <<";"<<X[k+1][1]<<")"<<endl;
//...........a...............
if( pow( ( pow((X[k+1][0]-X[k][0]),2)+pow((X[k+1][1]-X[k][1]),2) ),1/2.0)<E ){
cout <<"X(k+1) - X(k) = "<<pow( ( pow((X[k+1][0]-X[k+1][0]),2)+
pow((X[k+1][1]-X[k+1][1]),2) ),1/2.0);
Xz[0][0]=X[k+1][0];
Xz[0][1]=X[k+1][1];
}
//..................b.....................
if( pow( ( pow((X[k+1][0]-X[k][0]),2)+pow((X[k+1][1]-X[k][1]),2) ),1/2.0)>E ){
d[0][0]=d[n][0]=Y[n+1][0]-Y[1][0]; cout <<"d0 = ("<<d[0][0];
d[0][1]=d[n][1]=Y[n+1][1]-Y[1][1]; cout <<";"<<d[0][1]<<")"<<endl;
d[I[s]][0]=d[I[s]+1][0];
d[I[s]][1]=d[I[s]+1][1];
if( (d[1][0]*d[2][1]-d[1][1]*d[2][0]) != 0){
cout <<"rang(D1,...,Dn) = n"<<endl;
Y[0][0]=X[k+1][0]; cout <<"Y0 = ("<<Y[0][0]<<";";
Y[0][1]=X[k+1][1]; cout <<Y[0][1]<<")\n";
k=k+1;
I[s]=0;
goto TWO; }
if( (d[1][0]*d[2][1]-d[1][1]*d[2][0]) == n){
cout <<"rang(D1,...,Dn) < n"<<endl;
Y[0][0]=X[k+1][0];
Y[0][1]=X[k+1][1];
k=k+1; I[s]=0;
goto TWO;
}
}
cout<<endl<<endl<<"Iter - "<<iter<<endl;
cout<<endl<<endl<<endl<<endl<<endl;
cout<<"ANSWER"<<endl;
cout <<"\nXz("<<Xz[0][0]<<";"<<Xz[0][1]<<")"<<endl;
getch();
}
Результат:


Лабораторная работа № 4.
