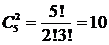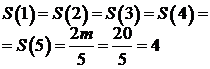Часть VI. Элементы теории графов.
Часть VI. Элементы теории графов.
Основные понятия теории графов.
Определение 1. Графом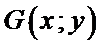 
называется совокупность 2-х множеств Х и У. Х - это множество точек, называемых вершинами графа, а У - это множество линий попарно соединяющие вершины и называемые ребрами или дугами.
Это определение можно сформулировать иначе: графом называется непустое множество точек (вершин) и отрезков (ребер), оба конца которых принадлежат заданному множеству точек.
В дальнейшем вершины графа мы будем обозначать латинскими буквами A, B, C, D. Иногда граф в целом будем обозначать одной заглавной буквой.
Определение 2.Вершины графа, которые не принадлежат ни одному ребру, называются изолированными.
Определение 3.Граф, состоящий только из изолированных вершин, называется нуль – графом.
Определение 4. Если рассматривается упорядоченное множество точек, т.е. на каждом ребре задается направление, то граф называется ориентированным; в противном случае граф называется неориентированным.
Определение 5. Сетью называется граф, в каждой дуге которого поставлено в соответствие некоторое число (или несколько чисел), которое называется весом дуги или ребра (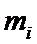 
). Например, расстояние между городами, стоимость прокладки дороги, потоки (пропускная способность дуги и т.д.).
Свойства вершин и ребер графа.
Определение 1. Ребра, имеющие одинаковые концевые точки называется параллельными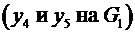 
.
Определение 2. Ребро, концевые вершины которого совпадают, называется петлей 
.
Определение 3. Вершина и ребро называются инцидентным друг другу, если вершина является для этого ребра концевой точкой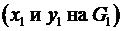 
.
Определение 4. Две вершины, являющиеся концевыми для некоторого ребра, называются смежными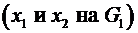 
.
Определение 5. Два ребра, инцидентные одной и той же вершине называется смежными ребрами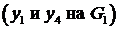 
.
Определение 6. Степенью вершины называется число ребер, инцидентных ей: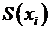 
, причем, если 
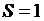, то вершина называется висячей 
, если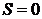 
, то вершина называется изолированной 
.
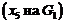Пример:
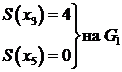
Теорема. В графе G сумма степеней всех его вершин - число четное, равное удвоенному числу ребер.
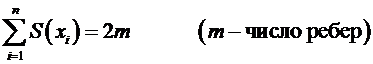
Пример:
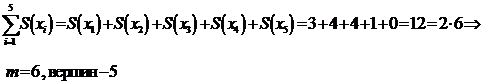
Определение 7. Граф называется полным, если любые две его различные вершины соединены ребром, и он не содержит параллельных ребер.
Определение 8. Дополнением графа G называется граф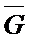 
с теми же вершинами, что и граф G и содержащий только те ребра, которые надо добавить графу G, чтобы получился полный граф.
Пример:
Построить полный граф для пяти вершин (n=5), число ребер равно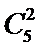 
.
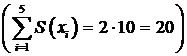
Пути и циклы графа.
Определение 1. Путем в графе называется такая последовательность ребер (дуг), ведущей от начала вершины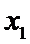 
в конечную вершину 
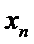, в которой каждые два соседних ребра имеют общую вершину, и никакое ребро не встречается два раза, т.е. такая последовательность дуг, при которой конец одной дуги является началом другой.
Например, на графе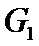 
:
от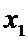 
до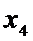 
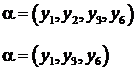
Определение 2. Циклом называется путь, начало, и конец которого совпадают:
Определение 3. Цикл называется простым, если он не проходит ни через одну вершину графа более одного раза.
Теорема. Для того чтобы граф представлял собой простой цикл, необходимо и достаточно, чтобы каждая его вершина имела степень равную двум, т.е.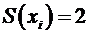 
.
Определение 4. Граф называется связным, если для любых двух его вершин существует соединяющий их путь, в противном случае граф - не связный: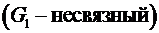 
, 
.
Определение 5. В общем случае несвязный граф является совокупностью связных графов, называемых компонентами.
, 
, 
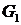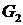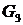- компоненты графа G.
§4. Способы задания графа.
Существует ряд способов задания графов. Для решения конкретной задачи можно выбрать тот или иной способ, в зависимости от удобства его применения.
Граф может быть задан:
Рисунком.
2. Перечислением вершин и ребер:
.
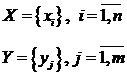Матрицей.
Пример: Пусть граф G имеет 4 вершины и 4 ребра, т.е.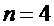 
и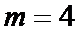 
. Задать граф можно:
1) Рисунком:
2) 
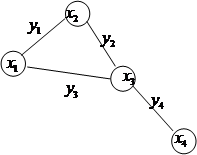Перечислением вершин и ребер:
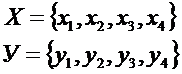
3) Матрицей:
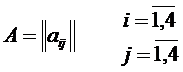
a) для неориентированного графа обычно задают матрицу смежности, элементы которой находятся по формуле:
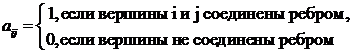
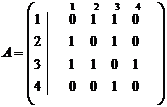
b) для ориентированных графов задается матрица инцидентности, элементы которой находят по формуле:
Пример: Построить матрицу инцидентности для графа:
 |
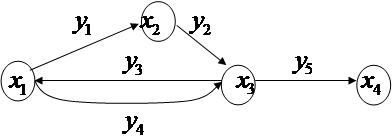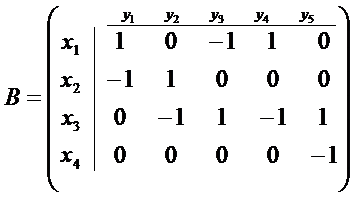
Замечание: Граф может быть задан и матрицей с весами на ребрах:
- если матрица симметричная, то граф неориентированный,
- если матрица несимметричная, то граф ориентированный.
Деревья.
Графы нашли применение практически во всех отраслях научных знаний: физике, биологии, химии, математике, истории, лингвистике, социальных науках, технике и т.п. Наибольшей популярностью теоретико-графовые модели пользуются при исследовании коммуникационных сетей, систем информатики, химических и генетических структур, электрических цепей и других систем сетевой структуры.
1. Задача коммивояжера (бродячий торговец, торговый агент): состоит в отыскании лучшего маршрута для коммивояжера, который должен объехать все порученные ему города и вернуться назад в кратчайший срок или с наименьшими затратами на проезд. Строго математически эта задача может быть сформулирована так: дана матрица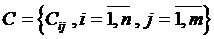 
расстояний между городам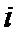и 
и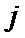 
, причем 
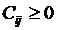. Среди замкнутых маршрутов 
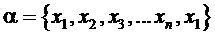, проходящих через каждый город только один раз, найти кратчайший путь, т.е. мы имеем задачу на экстремум:
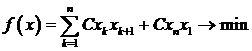
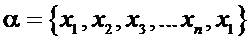
Матрица С может быть симметричной для любых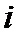 
и 
( 
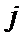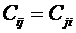для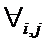 
) и может быть не симметричной, когда существуют 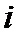и 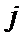, такие что 
.
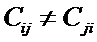Алгоритм задачи коммивояжера используется:
1) для выбора кратчайшего маршрута почтальона;
2) для составления проекта строительства дорог по минимальной стоимости, которую нужно проложить между «n» - городами;
3) для выбора маршрутов автотранспорта при кольцевой доставке товара;
4) для планирования производства на конвейерах;
Часть VI. Элементы теории графов.
Основные понятия теории графов.
Определение 1. Графом 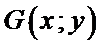называется совокупность 2-х множеств Х и У. Х - это множество точек, называемых вершинами графа, а У - это множество линий попарно соединяющие вершины и называемые ребрами или дугами.
Это определение можно сформулировать иначе: графом называется непустое множество точек (вершин) и отрезков (ребер), оба конца которых принадлежат заданному множеству точек.
В дальнейшем вершины графа мы будем обозначать латинскими буквами A, B, C, D. Иногда граф в целом будем обозначать одной заглавной буквой.
Определение 2.Вершины графа, которые не принадлежат ни одному ребру, называются изолированными.
Определение 3.Граф, состоящий только из изолированных вершин, называется нуль – графом.
Определение 4. Если рассматривается упорядоченное множество точек, т.е. на каждом ребре задается направление, то граф называется ориентированным; в противном случае граф называется неориентированным.
Определение 5. Сетью называется граф, в каждой дуге которого поставлено в соответствие некоторое число (или несколько чисел), которое называется весом дуги или ребра ( 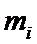). Например, расстояние между городами, стоимость прокладки дороги, потоки (пропускная способность дуги и т.д.).