Приближенные аналитические решения

(для средних значений при ):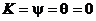

• автономный контур ИСК

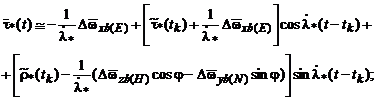
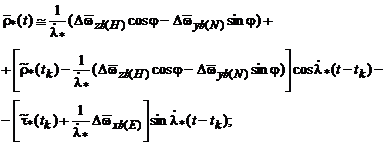(5.15)

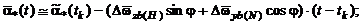
• автономный (недемпфируемый) контур вертикали

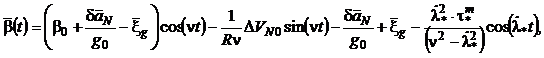
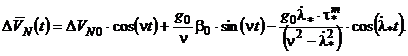(5.16)

• демпфируемый (при использовании скоростных измерений) контур вертикали

В этом случае согласно (5.12) модель погрешностей северного канала контура вертикали БИНС представим в виде

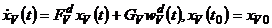, (5.17)

где

,

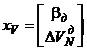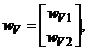
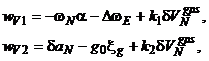
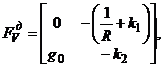
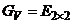. (5.18)

Собственные значения матрицы 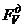найдем из характеристического уравнения 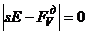или, при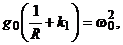 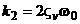, из уравнения:

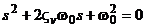. (5.19)

(заметим, что при 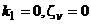имеем чисто колебательный контур 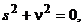где корни 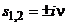, здесь 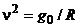– квадрат шулеровской частоты; т.е. система устойчива, но не асимптотически).

Корни уравнения (5.19) имеют вид 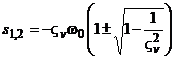или при 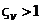, , 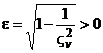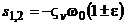. (5.20)

Легко видеть, что при 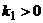, 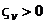система (5.17) обладает асимптотической устойчивостью. Причем если 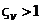, то переходный процесс в системе будет апериодическим, а если 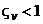– колебательным.

Переходная матрица стационарной системы (5.17) может быть найдена как обратное преобразование Лапласа 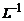обратной матрицы 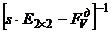(здесь s – оператор Лапласа), т.е.

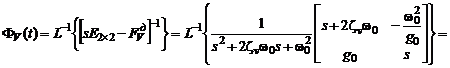
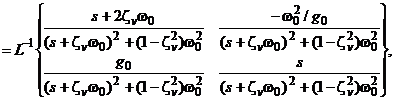(5.21)

Для минимизации времени начальной выставки аналога вертикали используется, как правило, так называемое жесткое демпфирование ( 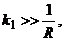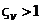). В этом случае переходная матрица состояния системы с учетом принятых допущений будет равна

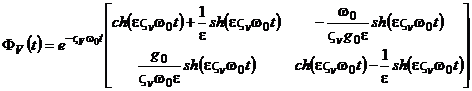. (5.22)

При 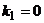имеет место слабое демпфирование, когда

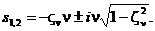
При 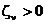система (5.3.9) обладает асимптотической устойчивостью. При этом также при 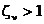переходный процесс в системе будет апериодическим, а при 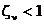- колебательным: 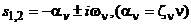с периодом

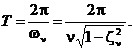
Переходная матрица состояния системы при 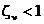в данном случае будет равна

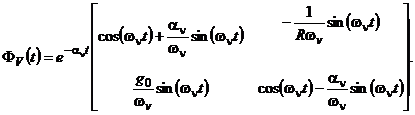(5.23)

Переходный процесс в системе из-за ненулевых начальных условий при 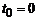в соответствии с (5.22) будет описываться следующим образом:

,

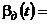
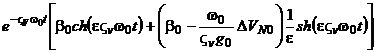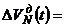
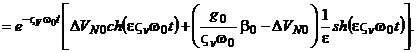
(5.24)

Время переходного процесса приближенно можно оценить из соотношения

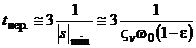, (5.25)

при этом для условий МПО оно может лежать в пределах нескольких минут.

П7. Программы read_1.m, BINS_LG_SRdr_o_Vidat_kz.m

Программа read_1.m

(загрузкив рабочую область Workspace Matlab массиваRez1.datрезультатов стендовых испытаний ИБ БИИМ на ЛГ)

d=fopen('d:\emlib\matlab\BINS_LG_KM\Rez1.dat','r');

f=zeros(7,1);

n=1800000;%4387680;

n0=2110;

f1=zeros(7,n-(n0-1));

dfx=zeros(1,n-(n0-1));

dfy=zeros(1,n-(n0-1));

dfz=zeros(1,n-(n0-1));

dr=zeros(1,n-(n0-1));

b1x=zeros(1,n-(n0-1));

b1y=zeros(1,n-(n0-1));

b1z=zeros(1,n-(n0-1));

fseek(d,2109*7*2,0);

for i=1:(n-(n0-1));

f=fread(d,7,'int16');

f1(:,i)=f(:,1);

End

fclose(d);

dfx=(f1(1,:)*4e-8)';

dfy=(f1(2,:)*4e-8)';

dfz=(f1(3,:)*1e-6)';

dr=(f1(4,:)*2e-6)';

b1x=(f1(5,:)*2e-6)';

b1y=(f1(6,:)*2e-6)';

b1z=(f1(7,:)*1e-5)';

time=0:0.005:n*0.005-0.005*n0;

time=time';

clear f1;

Программа BINS_LG_SRdr_o_Vidat_kz.m

загрузкив рабочую область Workspace Matlab массива необходимых констант (дискретность поступления данных ИБ на ЛГ, масштабные коэффициенты гироскопов и акселерометров и коэффициенты моделей их погрешностей, начальные значения параметров ориентации из режима «грубой» выставки и параметров движения объекта, параметры фигуры и гравитационного поля Земли и т.д.)

%параметры дискретизации данных

dt=0.005;

dT=0.005;

dT1=0.1;

Tz=1;

Tq=dT1;

%Характеристики нормальной Земли и нормального поля (межд.асамб.Люцерна, 1967)

U=7.2921151467e-5;

Om=U;

R=6371000;

go=9.780318;

bet=0.0053024;

bet_1=0.0000059;

%параметры общеземного эллипсоида

a=6378160;% большая полуось

al=1/298.26;% сжатие

b=a*(1-al);

e2=(a^2-b^2)/a^2;% квадрат эксцентриситета

%Координаты точки старта

fio=55.65;

lambdao=0;

ho=0;

% модель силы тяжести

ge_o=go*(1+bet*(sin(fio*pi/180))^2-bet_1*(sin(2*fio*pi/180))^2);

% параметры движения и ориентации

Vo=0;

dr_=0;

%real_1;

dro=6.904e-3;

Ko=71*pi/180+(25/60)*pi/180+(40/3600)*pi/180;

Bo=0*pi/180+(23/60)*pi/180+(34/3600)*pi/180;

Psio=Bo;

Ao=0*pi/180+((25/60)*pi/180)+(31/3600)*pi/180;

Tetao=-Ao;

OmEo=-Vo*cos(Ko)/R;

OmNo=U*cos(fio*pi/180)+(Vo*sin(Ko))/R;

OmHo=U*sin(fio*pi/180)+(Vo*sin(Ko)/R)*tan(fio*pi/180);

%Модель вертикальной качки

sigmaH=0.24;

lambdaH=0.82*2*pi/12;

MUH=0.21*lambdaH;

% Модель погрешностей значений эталонного курса на стенде

Sigma1DKs=30*5e-6;

MUDKs=1/3600;

Sigma2DKs=120*5e-6;

% Модель погрешностей лага

SigmaVTE=0.2;

MUVTE=1/5400;

SigmaVTN=0.2;

MUVTN=1/5400;

% Модель шумов измерений

SigmaZDVEGPS=0.1;

SigmaZDVNGPS=0.1;

SigmaZDVHGPS=0.1;

SigmaZDFiGPS=10/R;

SigmaZDLamGPS=10/(R*cos(fio*pi/180));

sigmaH=1;

tosrr=1;

DDVE=SigmaZDVEGPS^2*tosrr/Tz;

DDVN=SigmaZDVNGPS^2*tosrr/Tz;

DDVH=SigmaZDVHGPS^2*tosrr/Tz;

DDFi=SigmaZDFiGPS^2*tosrr/Tz;

DDLam=SigmaZDLamGPS^2*tosrr/Tz;

DDh2=sigmaH^2*tosrr/Tz;

DDKs=Sigma2DKs^2*tosrr/Tz;

SigmaZDVEL=0.3;

SigmaZDVNL=0.3;

tosrL=1;

DDVEL=SigmaZDVEL^2*tosrL/Tz;

DDVNL=SigmaZDVNL^2*tosrL/Tz;

% Начальные значения погрешностей БИНС (t=0)

Alphao=0*0.5*pi/180;

Betao=0*0.02*pi/180;

Gammao=0*-0.02*pi/180;

DVEo=0;

DVNo=0;

DVHo=0;

DFio=0*50*5e-6/30;

DLamo=0*-50*5e-6/30;

Dho=0*1;

X9o=[Alphao;Betao;Gammao;DVEo;DVNo;DVHo;DFio;DLamo;Dho];

VTEo=SigmaVTE;

VTNo=-SigmaVTN;

% начальные приборные значения

KO_prib=Ko+Alphao-tan(Psio)*(Betao*sin(Ko)+Gammao*cos(Ko));

PsiO_prib=Psio-Betao*cos(Ko)+Gammao*sin(Ko);

TetaO_prib=Tetao-(Betao*sin(Ko)+Gammao*cos(Ko))/cos(Psio);

c11=cos(KO_prib)*cos(TetaO_prib)+sin(KO_prib)*sin(PsiO_prib)*sin(TetaO_prib);

c12=sin(KO_prib)*cos(PsiO_prib);

c13=cos(KO_prib)*sin(TetaO_prib)-sin(KO_prib)*sin(PsiO_prib)*cos(TetaO_prib);

c21=-sin(KO_prib)*cos(TetaO_prib)+cos(KO_prib)*sin(PsiO_prib)*sin(TetaO_prib);

c22=cos(KO_prib)*cos(PsiO_prib);

c23=-(sin(KO_prib)*sin(TetaO_prib)+cos(KO_prib)*sin(PsiO_prib)*cos(TetaO_prib));

c31=-cos(PsiO_prib)*sin(TetaO_prib);

c32=sin(PsiO_prib);

c33=cos(PsiO_prib)*cos(TetaO_prib);

Coh_o=[c11 c12 c13

C21 c22 c23

c31 c32 c33];

Cbo_o=[cos(dr_),-sin(dr_),0

sin(dr_),cos(dr_), 0

0, 0, 1];

Cbh_o=Coh_o*Cbo_o;

L0=cos(KO_prib/2)*cos(PsiO_prib/2)*cos(TetaO_prib/2)+

+sin(KO_prib/2)*sin(PsiO_prib/2)*sin(TetaO_prib/2);

L1=cos(KO_prib/2)*cos(TetaO_prib/2)*sin(PsiO_prib/2)+

+sin(KO_prib/2)*sin(TetaO_prib/2)*cos(PsiO_prib/2);

L2=cos(KO_prib/2)*sin(TetaO_prib/2)*cos(PsiO_prib/2)-

-sin(KO_prib/2)*cos(TetaO_prib/2)*sin(PsiO_prib/2);

L3=cos(KO_prib/2)*sin(TetaO_prib/2)*sin(PsiO_prib/2)-

-sin(KO_prib/2)*cos(TetaO_prib/2)*cos(PsiO_prib/2);

Lho_o=[L0;L1;L2;L3];

LL=[L0,-L1,-L2,-L3;

L1, L0,-L3, L2;

L2, L3, L0,-L1;

L3,-L2, L1, L0];

Lob_o=[cos(dr_/2);

0;

0;

sin(dr_/2)];

Lhb_o=LL*Lob_o;

VE0_prib=Vo*sin(Ko)+DVEo;

VN0_prib=Vo*cos(Ko)+DVNo;

VH0_prib=DVHo;

FiO_prib=fio*pi/180+DFio;

Lam0_prib=lambdao*pi/180+DLamo;

h0_prib=ho+Dho;

% Априорные значения масштабных коэффициентов и параметров моделей акселерометров и гироскопов

k_aks=1;

DAxo=0;

DAyo=0;

DAzo=0;

DMax=0;

DMay=0;

DMaz=0;

Tet_axy=0;

Tet_axz=0;

Tet_ayx=0;

Tet_ayz=0;

Tet_azx=0;

Tet_azy=0;

k_gyr=1;

DGxo=0*5e-6;

DGyo=0*5e-6;

DGzo=0*5e-6;

DMgxo=0;

DMgyo=0;

DMgzo=0;

Tet_gxy=0;

Tet_gxz=0;

Tet_gyx=0;

Tet_gyz=0;

Tet_gzx=0;

Tet_gzy=0;

%Веса

weight_a=1;

weight_b=1;

weight_DV=1;

weight_DFi=1;

weight_DLa=1;

weight_Dh=1;

weight_Drx=1;

weight_Dry=1;

weight_Drz=1;

weight_Dnx=1;

weight_Dny=1;

weight_Dnz=1;

weight_DMgx=1;

weight_DMgy=1;

weight_DMgz=1;

weight_RDrX=1;

weight_RDrY=1;

weight_DVT=1;

%Управления

Znu=1.1;

Tp=600;

Om_v=2*pi/Tp;

k1=(Om_v^2-(go/R))/go;

k2=2*Znu*Om_v;

kz=0.1;

%k1=0;

%k2=2*Znu*sqrt(go/R);

%kz=0.03;

Литература

1. Анучин О.Н., Емельянцев Г.И. (под общей ред. акад. РАН В.Г.Пешехонова). Интегрированные системы ориентации и навигации для морских подвижных объектов. - СПб., 2004.

2. Программы:

· Stand.exe, программа для сбора данных с инерциальных датчиков и приемника GPS.

· Reader.exe, программа просмотра данных, записанных программой stand.exe с инерциальных датчиков и приемника GPS

· Комплекс программ для обработки данных в пакете Matlab, записанных программой stand.exe с инерциальных датчиков и приемника GPS.

3. Лекции проф. Емельянцева Г.И. (Электронная версия в сети ЦНИИ «Электроприбор», раздел 2 «Корабельные бескарданные инерциальные навигационные системы»).