П5. Модели погрешностей и аналитические решения
Классическая форма модели погрешностей
Линеаризованная относительно алгоритма идеальной работы модель погрешностей БИИМ в выработке параметров ориентации и навигационных параметров, включающая модели погрешностей в решении задач ориентации, преобразования сигналов акселерометров на навигационные оси и их интегрирования (вычисления составляющих векторов линейной скорости в проекциях на навигационные оси и географических координат места), может быть представлена с учетом управлений 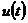 в следующем виде [1]:
в следующем виде [1]:
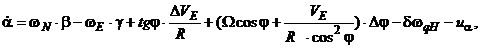
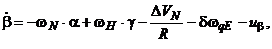

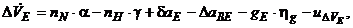
 (5.1)
(5.1)
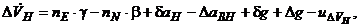
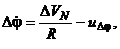
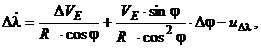
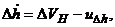
где
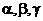 - погрешности БИИМ в аналитическом моделировании горизонтной системы координат с географической ориентацией осей (географического сопровождающего трехгранника)
- погрешности БИИМ в аналитическом моделировании горизонтной системы координат с географической ориентацией осей (географического сопровождающего трехгранника) 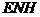 (рис. 5.1);
(рис. 5.1);

Рис.5.1. Погрешности БИИМ на ДУС в моделировании горизонтной системы координат с географической ориентацией осей 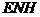
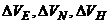 - погрешности в выработке составляющих вектора линейной скорости;
- погрешности в выработке составляющих вектора линейной скорости;
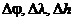 - погрешности в выработке географических широты, долготы и высоты места;
- погрешности в выработке географических широты, долготы и высоты места;
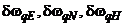 - проекции нескомпенсированных дрейфов ДУС и так называемых "вычислительных" дрейфов на оси горизонтной системы координат;
- проекции нескомпенсированных дрейфов ДУС и так называемых "вычислительных" дрейфов на оси горизонтной системы координат; 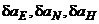 - проекции инструментальных погрешностей акселерометров на оси горизонтной системы координат;
- проекции инструментальных погрешностей акселерометров на оси горизонтной системы координат; 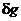 - погрешность компенсации вертикальной составляющей вектора нормальной силы тяжести, обусловленная погрешностями знания координат места;
- погрешность компенсации вертикальной составляющей вектора нормальной силы тяжести, обусловленная погрешностями знания координат места;  ,
, 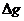 - составляющие уклонения отвесной линии (УОЛ) и аномалия силы тяжести;
- составляющие уклонения отвесной линии (УОЛ) и аномалия силы тяжести; 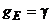 - ускорение силы тяжести нормальной Земли;
- ускорение силы тяжести нормальной Земли; 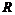 - средний радиус Земли;
- средний радиус Земли; 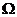 - угловая скорость суточного вращения Земли;
- угловая скорость суточного вращения Земли; 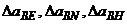 - погрешности компенсации ”вредных” ускорений по соответствующим осям, выражения для которых имеют вид:
- погрешности компенсации ”вредных” ускорений по соответствующим осям, выражения для которых имеют вид:

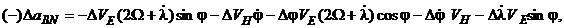 (5.2)
(5.2)
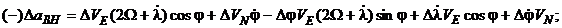
 - составляющие угловой скорости вращения горизонтного трехгранника с географической ориентацией осей, которые определяются как
- составляющие угловой скорости вращения горизонтного трехгранника с географической ориентацией осей, которые определяются как
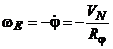 ,
, 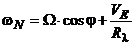 ,
, 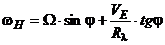 , (5.3)
, (5.3)
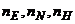 - проекции кажущегося ускорения на оси горизонтной системы координат, которые определяются выражениями:
- проекции кажущегося ускорения на оси горизонтной системы координат, которые определяются выражениями:
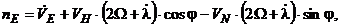
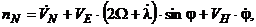 (5.4)
(5.4)
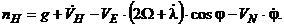
Аналоговая форма модели погрешностей
Кинематические соотношения[1]:
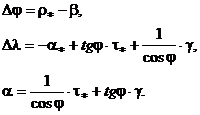 (5.5)
(5.5)
где 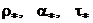 - погрешности аналога ИСК (рис.5.2)
- погрешности аналога ИСК (рис.5.2)
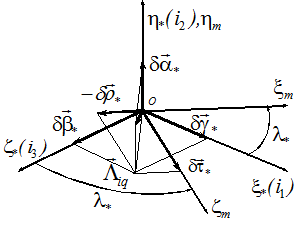
Рис.5.2. Погрешности БИИМ в моделировании инерциальной системы координат 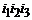 в проекциях на оси экваториальной системы координат
в проекциях на оси экваториальной системы координат 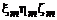
Модель погрешностей аналога инерциальной системы координат (ИСК)
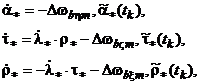 (5.6)
(5.6)
где  - проекции нескомпенсированных дрейфов ДУС и так называемых "вычислительных" дрейфов на оси экваториальной системы координат
- проекции нескомпенсированных дрейфов ДУС и так называемых "вычислительных" дрейфов на оси экваториальной системы координат 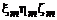 , определяемые из следующих соотношений:
, определяемые из следующих соотношений:
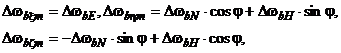 (5.7)
(5.7)
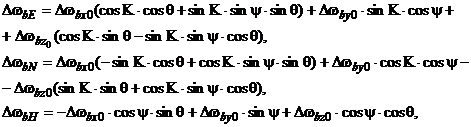 (5.8)
(5.8)
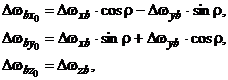 (5.9)
(5.9)
здесь 
 и
и 
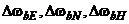 - проекции вектора
- проекции вектора  нескомпенсированных дрейфов ДУС соответственно на оси связанной с объектом системы координат
нескомпенсированных дрейфов ДУС соответственно на оси связанной с объектом системы координат 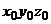 и на оси горизонтной системы координат с географической ориентацией осей
и на оси горизонтной системы координат с географической ориентацией осей 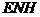 ;
;
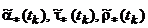 - начальные значения погрешностей на момент окончания решения задачи точной выставки БИИМ.
- начальные значения погрешностей на момент окончания решения задачи точной выставки БИИМ.
Модель погрешностей ДУС (ЛГ и ВОГ)
Модель дрейфов ДУС может быть аппроксимирована в виде суммы нескольких составляющих:
· погрешности калибровки начального смещения “нуля” и его нестабильности в пуске, т.е. погрешности практически постоянной на достаточно длительном интервале времени, которую вследствие отсутствия данных о спектре ее изменчивости целесообразно описывать винеровским процессом при соответствующих начальных условиях;
· погрешности масштабного коэффициента, которая определяет составляющую, пропорциональную измеряемой величине;
· погрешности знания румбовых дрейфов ВОГ, которые обусловлены влиянием внешнего магнитного поля и могут быть представлены в виде первой гармоники от угла поворота ИБ;
· составляющей, обусловленной неортогональностями осей измерительного блока ДУС;
· “шумовой” составляющей, характеризующей флуктуационные погрешности гироскопов
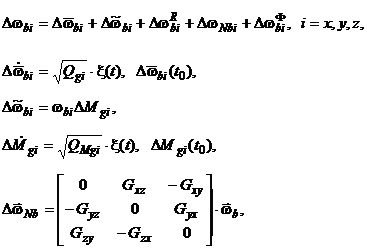 (5.10)
(5.10)
где
 – квазисистематическая составляющая с начальным уровнем
– квазисистематическая составляющая с начальным уровнем 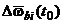 , характеризуемым погрешностью калибровки смещения “нуля” ДУС от пуска к пуску, и интенсивностью
, характеризуемым погрешностью калибровки смещения “нуля” ДУС от пуска к пуску, и интенсивностью 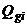 , обусловленной нестабильностью смещения “нуля” в пуске из-за температурных деформаций гироскопа;
, обусловленной нестабильностью смещения “нуля” в пуске из-за температурных деформаций гироскопа; 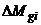 – погрешность масштабного коэффициента гироскопа, а
– погрешность масштабного коэффициента гироскопа, а 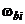 - измеряемая им угловая скорость;
- измеряемая им угловая скорость; 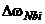 - составляющие, обусловленные неортогональностями
- составляющие, обусловленные неортогональностями  (аппроксимированными соответствующими винеровскими процессами) осей измерительного блока ДУС;
(аппроксимированными соответствующими винеровскими процессами) осей измерительного блока ДУС; 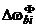 - ”белошумная” составляющая c интенсивностью
- ”белошумная” составляющая c интенсивностью  ;
; 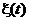 - “белый” шум единичной интенсивности;
- “белый” шум единичной интенсивности;
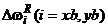 - румбовые дрейфы ВОГ, которые могут быть представлены первой гармоникой разложения в ряд Фурье:
- румбовые дрейфы ВОГ, которые могут быть представлены первой гармоникой разложения в ряд Фурье:
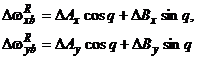 ;
;  - в условиях стенда;
- в условиях стенда; 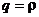 - на объекте;
- на объекте;
здесь 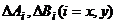 - искомые коэффициенты разложения, аппроксимированные соответствующими винеровскими процессами; здесь
- искомые коэффициенты разложения, аппроксимированные соответствующими винеровскими процессами; здесь 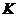 - курс,
- курс, 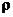 - угол поворота ИБ относительно корпуса БИИМ.
- угол поворота ИБ относительно корпуса БИИМ.
Для ДНГ следует учесть в модели (5.10) дополнительные составляющие дрейфа [1], зависящие от линейных ускорений 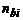 , действующих по осям измерительного блока
, действующих по осям измерительного блока 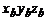 . Так, например, если считать, что кинетический момент ДНГ направлен по оси
. Так, например, если считать, что кинетический момент ДНГ направлен по оси 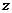 , то его погрешности измерения угловой скорости по осям
, то его погрешности измерения угловой скорости по осям  и
и 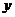 , обусловленные действующими на его линейными ускорениями, имеют вид
, обусловленные действующими на его линейными ускорениями, имеют вид
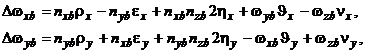 (5.11)
(5.11)
где  - дрейфы от осевого дебаланса ротора, для современных ДНГ порядка 2 0/ч/g;
- дрейфы от осевого дебаланса ротора, для современных ДНГ порядка 2 0/ч/g; 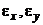 - квадратурные составляющие порядка 1.5 0/ч/g;
- квадратурные составляющие порядка 1.5 0/ч/g; 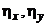 - составляющие дрейфа из-за неравножесткости подвеса порядка 0.2 0/ч/g2;
- составляющие дрейфа из-за неравножесткости подвеса порядка 0.2 0/ч/g2;  - углы, характеризующие отклонения осей чувствительности ДНГ от их номинальных направлений (корпусные оси
- углы, характеризующие отклонения осей чувствительности ДНГ от их номинальных направлений (корпусные оси 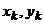 ) в плоскости, ортогональной вектору
) в плоскости, ортогональной вектору 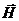 гироскопа, могут достигать 1.50;
гироскопа, могут достигать 1.50; 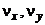 - углы, характеризующие отклонения вектора
- углы, характеризующие отклонения вектора 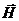 гироскопа от корпусной оси
гироскопа от корпусной оси 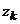 , не превышают 0.20;
, не превышают 0.20; 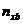 ,
, 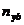 ,
, 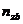 - составляющие вектора
- составляющие вектора 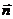 кажущегося ускорения.
кажущегося ускорения.
