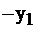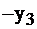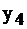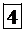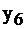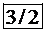Экономическая интерпретация двойственной задачи
И теории двойственности
Исходная задача I имела следующий экономический смысл: основные переменные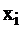 
обозначали количество произведенной продукции i-го вида, дополнительные переменные обозначали излишек соответствующего вида ресурсов, каждое из неравенств выражало собой расход определенного вида сырья в сравнении с запасом этого сырья. Целевая функция определяла прибыль при реализации всей продукции. Предположим теперь, что предприятие имеет возможность реализовывать сырье на сторону. Поставим вопрос: какую минимальную цену надо установить за единицу каждого вида сырья при условии, что доход от реализации всех его запасов должен быть не меньше дохода от реализации продукции, которая может быть выпущена из этого сырья. Иначе говоря, выгодно было бы продавать сырье, чем производить изделия. Переменные двойственной задачи 
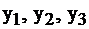имеют смысл – это условные относительные (теневые) цены за ресурсы 1, 2, 3 вида соответственно. Тогда доход от продажи видов сырья, расходуемого на производство одной единицы продукции I, равен: 
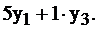Но, если мы хотим, чтобы доход от продажи сырья был не меньше, чем от реализации продукции, то должно быть 
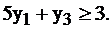Именно в силу такого экономического толкования система ограничений двойственной задачи принимает вид
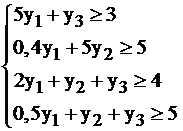
А целевая функция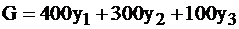 
подсчитывает условную суммарную стоимость всего имеющегося сырья. Понятно, что в силу I теоремы двойственности 
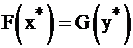равенство означает, что максимальная прибыль от продажи всей готовой продукции совпадает с минимальной условной ценой ресурсов. Итак, условные оптимальные цены 
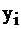показывают наименьшую стоимость ресурсов, при которой выгодно обращать эти ресурсы в продукцию, т.е. производить. Величина 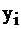показывает насколько увеличится значение целевой функции, если запас сырья увеличить на 1 ед.
Еще раз обратим внимание на то, что 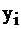– это лишь условные, предполагаемые, а не реальные цены на сырье. Иначе, читателю может показаться странным, что например, 
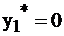. Этот факт вовсе не означает, что реальная цена 1–го ресурса нулевая, ничего бесплатного в этом мире нет. Равенство нулю условной цены означает лишь, что этот ресурс не израсходован полностью, имеется в излишке, недефицитен. Действительно, посмотрим на 1-е неравенство в системе ограничений задачи I, в котором подсчитывается расход 1-го ресурса: 
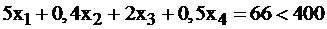. Его избыток составляет 
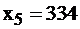ед. при данном оптимальном плане производства, и поэтому для производителя он недефицитен, его условная цена равна 0, его не надо закупать. Наоборот, ресурсы 2-й и 3-й используются полностью, причем 
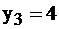а 
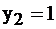, т.е. сырье третьего вида более дефицитно, чем второго, его условная цена больше. Если производитель продукции имел бы возможность приобретать дополнительно сырье к уже имеющемуся, с целью получения максимального дохода от производства, то, увеличив сырье 2-го вида на 1 единицу, он бы получил дополнительно доход в 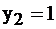денежных единиц, а увеличив на 1 ед. сырье 3-го вида, значение целевой функции увеличилось бы на 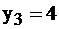ед.
Если перед производителем стоит вопрос: «выгодно ли производить какую-либо новую продукцию, при условии, что затраты на 1 единицу продукции составят 3, 1, 4 единицы сырья соответственно, а прибыль от реализации равна 23 единицам?», то в силу экономического истолкования задачи ответить на этот вопрос несложно. Поскольку затраты и условные цены ресурсов известны: затраты равны 3, 1, 4, а цены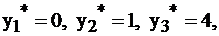 
значит можно посчитать суммарную условную стоимость ресурсов, необходимых для производства этой новой продукции: 
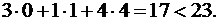Т.е. продукцию производить выгодно, т.к. прибыль от реализации превышает затраты на ресурсы, в противном случае, ответ бы на этот вопрос был отрицательным.
Замечание. Иногда при решении задач ЛП применяют двойственный симплекс-метод. Этот метод удобно применять при решении задачи о рационе, задачи о раскрое и некоторых других. Поскольку, решая исходную задачу, мы автоматически получаем решение двойственной, то иногда удобно выбирать, какую из задач решать. Двойственный симплекс–метод основан на очень простой идее. К данной задаче нужно построить двойственную, решить двойственную, а затем по её решению найти решение исходной.
Можно продемонстрировать на примере уже рассмотренной нами задачи о рационе.
I. 
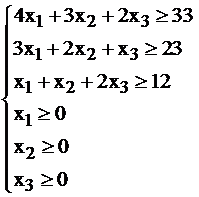II.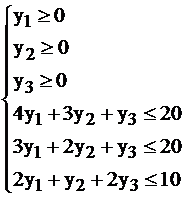 
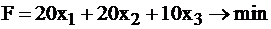
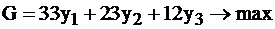
Решаем симплекс–методом задачу II (смотри табл.2.17-19).
Таблицы 2.17 Таблица 2.18
|
|
Таблица 2.19
| Баз. | 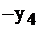 | 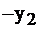 | 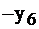 | Своб. |
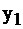 | -1/6 | |||
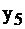 | -1/6 | |||
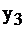 | -1/3 | 1/3 | 2/3 | |
 | 1/2 | 5/2 |
Выписываем решение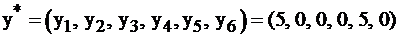 
. Найдем решение исходной, пользуясь II теоремой двойственности.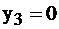 
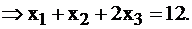
Так как неравенств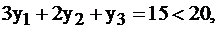о 
то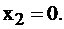 
Найдем 
и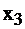 
из системы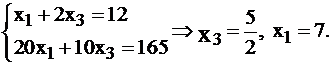 
Итак,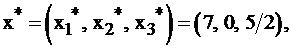 
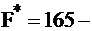решение исходной задачи о рационе.
Еще раз отметим, что мы воспользовались тем, что двойственная задача имела специальный вид, и ее удобно было решать, а затем уже вернуться к исходной. Но в силу тесной связи между этими двумя парами задач, на самом деле симплекс–таблицы, полученные сейчас, и ранее см.§ 2.7, совпадают с точностью до транспонирования. Фактически мы лишь упростили внешний вид табл. 2.10-2.12, избавив себя от излишних «минусов».
ГЛАВА III