Исходная задача I Двойственная задача II

Напомним, что транспонированной называется матрица, у которой строки и столбцы меняются местами. Поэтому коэффициенты при переменных 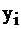в задаче II – это соответственно коэффициенты го неравенства в задаче I.

Неравенства, соединенные стрелочками, будем называть сопряженными.

Теоремы двойственности

Двойственность является фундаментальным понятием в теории линейного программирования. Основные результаты теории двойственности заключены в двух теоремах, называемых теоремами двойственности.

Теорема 1 (первая теорема двойственности).

Если одна из пары двойственных задач I и II разрешима, то разрешима и другая, причем значения целевых функций на оптимальных планах совпадают, 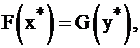где 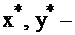оптимальные решения задачи I и II.

Теорема 2(вторая теорема двойственности).

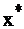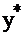Планы и оптимальны в задачах I и II тогда и только тогда, когда при подстановке их в систему ограничений задачи I и II соответственн, хотя бы одно из любой пары сопряженных неравенств обращается в равенство.

Доказательства теорем опускаем, а на конкретном примере нашей задачи покажем, как они работают. Теорема 2 позволяет по решению одной задачи находить решение двойственной.

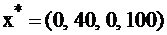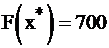Итак, имеем оптимальное решение и задачи I. Найдем решение двойственной задачи II 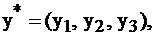не прибегая к симплекс-методу, а воспользовавшись второй теоремой двойственности и известным оптимальным планом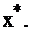

Для этого необходимо подставить оптимальное решение 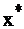в каждое неравенство системы ограничений и посмотреть, как оно выполняется: строго или нет.

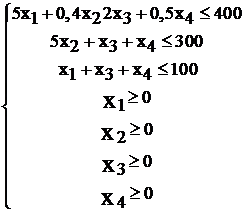
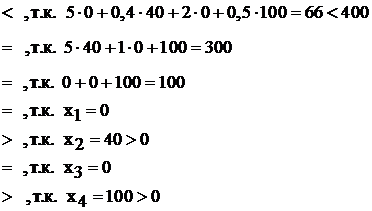
Поскольку 1, 5, 7 неравенства строгие (имеют знак «<» или «>»), то соответствующие им неравенства в задаче II из пары сопряженных по II теореме двойственности обязаны обратиться в равенства, имеем:

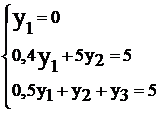Решаем систему, находим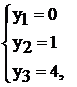

т.е. 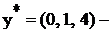оптимальное решение. Заметим, что действительно I-я теорема двойственности справедлива: .

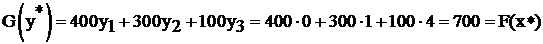Итак, в силу второй теоремы двойственности, мы быстро нашли оптимальное решение задачи II, пользуясь условием обращения в равенство хотя бы одного из пары сопряженных неравенств в системах ограничений двойственных задач.

Между переменными исходной задачи и переменными двойственной существует связь. А именно, после приведения обеих задач I и II к каноническому виду основные и дополнительные переменные задач соответствуют друг другу следующим образом:

основные дополнительные

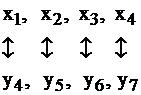
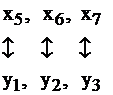
дополнительные основные

Установив такую связь, внимательный читатель заметит, что, решив задачу I симплекс-методом, и получив последнюю симплекс–таблицу (табл. 2.15), мы фактически решим и задачу II. Запишем таблицу 2.16, учитывая соответствие между переменным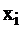и и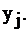

Таблица 2.16

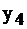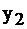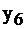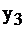свободные базис		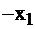		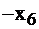	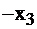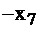правые части

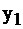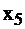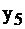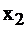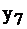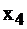Если последняя симплекс-таблица известна, то, пользуясь соответствием, можно найти решение двойственной задачи. Переменные, которые в левом столбце: 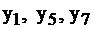обязаны равняться 0, т.к. 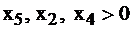строго. А переменные из верхней строки 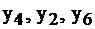принимают значения нижней строки 1, 1, 0, 4 соответственно, т.к. им соответствующие переменные 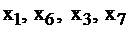равны 0 как свободные. Итак, из последней таблицы задачи II, не проводя никаких вычислений, и пользуясь лишь соответствием переменных, можно определить 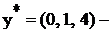оптимальное решение.

Необходимо знать оба способа решения двойственной задачи. Т.к. если исходная задача решалась на компьютере, например, в приложении Excel , и вы не имеете симплекс-таблиц, но знаете оптимальный план, по второй теореме двойственности найдете решение. Если же вы находили исходный план вручную, нет необходимости решать систему линейных уравнений, достаточно посмотреть в последнюю симплекс-таблицу. Итак, мы научились по решению исходной задачи находить решения двойственной. Это возможно благодаря глубокой связи между переменным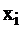и и 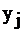. Осталось разобраться, каково экономическое содержание этих взаимосвязей.