Двойственность в линейном программировании
Каждой задаче линейного программирования можно поставить в соответствие другую задачу линейного программирования – двойственную. Решая одну из них, автоматически решается и другая задача. Такие задачи называют взаимно двойственными. Двойственные задачи имеют важный экономический смысл, теория двойственности позволяет найти некоторые экономические характеристики производственных процессов, провести анализ на чувствительность.
Рассмотрим задачу о планировании производства, решим ее прямым симплекс-методом. А затем построим и решим двойственную ей задачу, обсудим экономический смысл полученных результатов.
Задача 8 (о плане). Предприятие располагает тремя видами сырья и намеревается выпускать четыре вида продукции. Технологические коэффициенты в таблице (табл.2.12) указывают затраты соответствующего вида сырья на 1 единицу определенного вида продукции, а также прибыль от реализации 1 единицы продукции и общие запасы ресурсов. Найти оптимальный план производства продукции, при котором будет обеспечена максимальная прибыль.
Таблица 2.12
 сырье сырье | изделия | I | II | II | IV | Запасы сырья |
| 0,4 | 0,5 | |||||
| Прибыль |
Составим математическую модель. Пусть 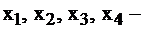 количество продукции I, II, III, IV вида соответственно в плане. Тогда количество используемого сырья и его запасы выразятся в неравенствах:
количество продукции I, II, III, IV вида соответственно в плане. Тогда количество используемого сырья и его запасы выразятся в неравенствах:
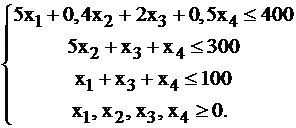
 .
.
Целевая функция выражает собой общую суммарную прибыль, полученную от реализации всей плановой продукции. А каждое из неравенств выражает затраты определенного вида сырья. Понятно, что затраты не должны превышать запасов сырья.
Приведем задачу к канонической форме, введя дополнительные переменные 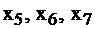 в каждое из неравенств. Очевидно, что, если 1-го ресурса необходимо для производства плановой продукции
в каждое из неравенств. Очевидно, что, если 1-го ресурса необходимо для производства плановой продукции 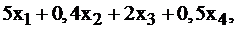 то
то 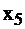 обозначает излишки 1-го ресурса как разность между имеющимся запасом и требуемым для производства. Аналогично
обозначает излишки 1-го ресурса как разность между имеющимся запасом и требуемым для производства. Аналогично 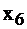 и
и 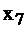 . Итак, дополнительные переменые задачи ЛП обозначают излишки сырья, времени, других ресурсов, остающихся в производстве для данного оптимального плана.
. Итак, дополнительные переменые задачи ЛП обозначают излишки сырья, времени, других ресурсов, остающихся в производстве для данного оптимального плана.
Запишем задачу в таблицу, предварительно выписав ее каноническую форму.
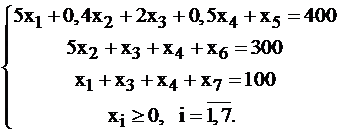
 .
.
I этап. Эта задача специального вида, базис составляют переменные 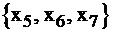 , правые части уравнений неотрицательны, опорный план
, правые части уравнений неотрицательны, опорный план 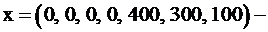 допустимый. Он соответствует симплекс-таблице (табл.2.13).
допустимый. Он соответствует симплекс-таблице (табл.2.13).
Таблица 2.13
| свободные базис | 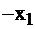 | 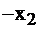 | 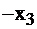 | 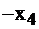 | правые части |
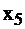 | 0,4 | 0,5 | |||
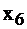 | |||||
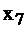 | 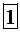 |  100 100 | |||
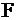 | -3 | -5 | -4 | -5 |

II этап. Проверим план на оптимальность. Так как в индексной F–строке есть отрицательные элементы, то план не оптимален, переходим к III этапу.
III этап. Улучшение опорного плана. Выберем в качестве разрешающего столбца четвертый, могли выбрать и второй, т.к. в обоих – 5. Выберем в качестве разрешающего элемента 1, т.к. именно на нем достигается минимум отношений 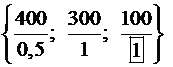 . С разрешающим элементом
. С разрешающим элементом 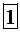 проводим преобразование таблицы по правилам 3.1–3.5 (табл.2.14).
проводим преобразование таблицы по правилам 3.1–3.5 (табл.2.14).
Таблица 2.14
| свободные базис | 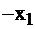 | 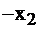 | 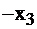 | 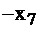 | правые части |
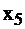 | 4,5 | 0,4 | 1,5 | -0,5 | |
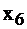 | -1 | 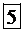 | -1 | -1 |  200 200 |
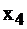 | |||||
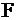 | 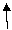 -5 -5 |
Полученный план опять не оптимален, т.к. в 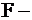 строке есть отрицательный элемент –5, этот столбец разрешающий. В качестве разрешающего элемента выбираем 5, т.к.
строке есть отрицательный элемент –5, этот столбец разрешающий. В качестве разрешающего элемента выбираем 5, т.к. 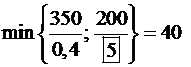 .
.
Пересчитываем еще раз таблицу. Заметим, что пересчет удобно начинать с индексной строки, т.к. если в ней все элементы неотрицательны, то план оптимален, и чтобы его выписать, достаточно пересчитать столбец свободных членов, нет необходимости вычислять «внутренность» таблицы. Результаты запишем в таблицу 2.15.
Таблица 2.15
| свободные базис | 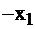 | 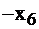 | 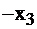 | 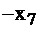 | правые части |
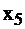 | |||||
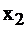 | |||||
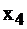 | |||||
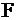 |
План оптимален, т.к. в индексной строке нет отрицательных элементов, выписываем его.
IV этап. Базисные переменные 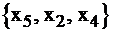 принимают значения из столбца свободных членов, а свободные переменные равны 0. Итак, оптимальный план
принимают значения из столбца свободных членов, а свободные переменные равны 0. Итак, оптимальный план 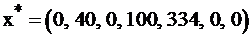 и
и 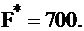
Действительно, 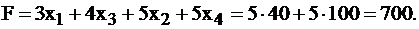 Т.е. для получения максимальной прибыли в 700 руб., предприятие должно выпускать изделия II вида в количестве 40 штук, IV вида в количестве 100 штук, изделия I, III видов производить невыгодно. При этом напомним смысл дополнительных переменных – это излишки сырья, следовательно, сырье 2–го и 3–го видов будет израсходовано полностью, а сырья 1-го вида останется 334 единицы, т.к.
Т.е. для получения максимальной прибыли в 700 руб., предприятие должно выпускать изделия II вида в количестве 40 штук, IV вида в количестве 100 штук, изделия I, III видов производить невыгодно. При этом напомним смысл дополнительных переменных – это излишки сырья, следовательно, сырье 2–го и 3–го видов будет израсходовано полностью, а сырья 1-го вида останется 334 единицы, т.к. 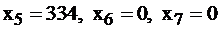 .
.
Сформулируем правила построения двойственной задачи.
1. Количество переменных в двойственной задаче равно количеству неравенств в исходной (без учета неравенств неотрицательности).
2. Матрица коэффициентов двойственной задачи является транспонированной к матрице коэффициентов исходной.
3. Столбец свободных членов исходной является строкой коэффициентов для целевой функции двойственной и наоборот.
4. Целевая функция в одной задаче максимизируется, в другой минимизируется.
5. Условиям неотрицательности переменных исходной задачи соответствуют неравенства-ограничения двойственной, направленные в другую сторону. Ограничению типа равенства соответствует переменная без знака.
При записи задач их следуетужно располагать рядом друг с другом, точно определяя соответствие неравенств (показано стрелочками).
