Постановка и математическая модель замкнутой транспортной задачи, число базисных неизвестных. Записать основные свойства этой модели.
Транс.задача формулируется следующим образом. Продукт, сосредоточенный в m пунктах производства в кол-ве a1, a2,...,am единиц, необходимо распределить между n пунктами потребления, которым необходимо b1,b2,..,bn единиц. Стоимость перевозки единицы продукта из i-го пункта пр-ва в j-ый пункт потр-ия равна cij. Необходимо составить план перевозок, при кот. запросы всех пунктов потребления были бы удовлетворены за счет имеющихся продуктов в пунктах пр-ва и общие транспортные расходы по доставке были бы минимальны.
Обозначим xij кол-во груза, планируемого к перевозке от i-го поставщика j-му потребителю.При балансе произ-ва и потр-я 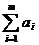 =
= 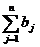 математическая модельтр. задачи выглядит так: найти план перевозок Х=(хij), i=1,2,..,m; j=1,2,..,n, минимизирующий общую стоимость всех перевозок L=
математическая модельтр. задачи выглядит так: найти план перевозок Х=(хij), i=1,2,..,m; j=1,2,..,n, минимизирующий общую стоимость всех перевозок L= 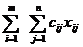 ,при условии что из любого пункта вывозится весь продукт:
,при условии что из любого пункта вывозится весь продукт: 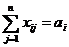 , i=1,2,..,m. И любому потребителю доставляется необходимое количество груза:
, i=1,2,..,m. И любому потребителю доставляется необходимое количество груза: 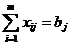 j=1,2,..,n,.. и по смыслу задачи x11>0,..,xmn>0.
j=1,2,..,n,.. и по смыслу задачи x11>0,..,xmn>0.
Если оно не выполнено, то задача не закрыта. Чтобы ее закрыть, нужно ввести фиктивного потребителя.
Преобразование открытой модели в закрытую.Если общий объем производства превышает объем, требуемый всем потребителям, то модель задачи открытая. Для превращения ее в закрытую вводим фиктивный пункт потребления с объемом потребления, равным разнице между объемом пр-ва и потр-я.
Постановка и математическая модель транспортной задачи, в которой суммарные запасы продукции меньше суммарных запросов на нее. Записать правила сведения такой модель к замкнутой задаче и записать полученную замкнутую модель транспортной задачи.
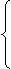 Если
Если 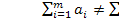 , то транспортная задача является незамкнутой. Пусть
, то транспортная задача является незамкнутой. Пусть 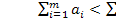 , т.е. суммарные запасы продукции меньше суммарных потребностей в ней и математическая модель открытой ТЗ имеет вид: найти наименьшее значение функции L=
, т.е. суммарные запасы продукции меньше суммарных потребностей в ней и математическая модель открытой ТЗ имеет вид: найти наименьшее значение функции L= 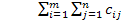 min при ограничениях:
min при ограничениях: 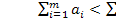 ,
,
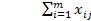 , j=1,…,n,
, j=1,…,n,
 =
=  , i=1,…,m
, i=1,…,m
 , i=1,…,m; j=1,…,n.
, i=1,…,m; j=1,…,n.
Если безразлично, какой из потребителей недополучит продукцию, то ТЗ сводится к закрытой замкнутой модели путём введения дополнительного фиктивного (m+1)-ого поставщика с запасом продукции, равным 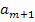 =
= 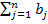 -
- 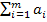 . При этом значения тарифов
. При этом значения тарифов 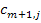 полагаем равными нулю, что обеспечивает равенство целевых функций исходных и соответствующих им вспомогательных задач. В итоге получаем замкнутую модель ТЗ. Математическая модель ТЗ: найти план перевозок X=(
полагаем равными нулю, что обеспечивает равенство целевых функций исходных и соответствующих им вспомогательных задач. В итоге получаем замкнутую модель ТЗ. Математическая модель ТЗ: найти план перевозок X=( 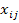 ), i=1,2,…,m; j=1,2,…,n, минимизирующий общую стоимость всех перевозок L=
), i=1,2,…,m; j=1,2,…,n, минимизирующий общую стоимость всех перевозок L= 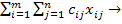 min при условии, что из любого пункта производства вывозится весь продукт:
min при условии, что из любого пункта производства вывозится весь продукт: 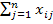 =
= 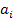 , i=1,2,…,m и любому потребителю доставляется необходимое количество груза:
, i=1,2,…,m и любому потребителю доставляется необходимое количество груза: 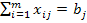 , j=1,2,…,n, причём по смыслу задачи
, j=1,2,…,n, причём по смыслу задачи 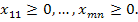 Решаем её, находим оптимальный план. При этом значения
Решаем её, находим оптимальный план. При этом значения 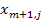 в решении вспомогательной задачи будут обозначать величину неудовлетворённого спроса j-ого потребителя.
в решении вспомогательной задачи будут обозначать величину неудовлетворённого спроса j-ого потребителя.
Постановка и математическая модель транспортной задачи, в которой суммарные запасы продукции больше суммарных запросов на нее. Записать правила сведения такой задачи к замкнутой и записать полученную замкнутую модель транспортной задачи.
Пусть 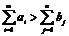 , т е суммарные запасы продукции больше суммарных потребностей в ней. Если безразлично, у кого из поставщиков останутся излишки продукции, то решение такой несбалансированной задачи сводится к решению замкнутой транспортной задачи путем введения дополнительного фиктивного (n-1)го потребителя, запросы которого составляют
, т е суммарные запасы продукции больше суммарных потребностей в ней. Если безразлично, у кого из поставщиков останутся излишки продукции, то решение такой несбалансированной задачи сводится к решению замкнутой транспортной задачи путем введения дополнительного фиктивного (n-1)го потребителя, запросы которого составляют
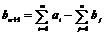
Значение сi, n+1 полагаем равным нулю и решаем вспомогательную задачу с n+1 потребителем и m поставщиками. При этом продукция xi,n+1 , планируемая для перевозки к фиктивному потребителю, остается на i-м складе.
