В каких задачах применяется симплекс-метод?

В задачах линейного программирования. Для задач, связанных с принятием решений в экономике, когда требуется достичь некоторой цели при ограниченных ресурсах. Если функция цели линейно зависит от переменных (размеров видов деятельности или производственных процессов) и расходы ресурсов также линейно зависят от переменных, то такая задача принятия решений сводится к задаче линейного программирования (ЛП)

36. Что представляет собой симплексная таблица?

Симплекс-таблица составляется из коэффициентов при x₁, x₂, x₃, x₄ и чисел, стоящих в правых частях уравнений-ограничений задачи: в первой строке записываются элементы уравнения (А), во второй - (В). В последней строке симплекс-таблицы записываются коэффициенты и правая часть целевой функции (С). Таким образом, симплекс-таблица содержит две строки коэффициентов (по числу ограничений задачи) и строку коэффициентов целевой функции. Число столбцов в симплекс-таблице равно числу переменных задачи плюс один столбец правых частей (b).

Запишите симметричную пару двойственных задач линейного программирования.

Z=c1x1+c2x2+…+cnxn → max F=b1y1+b2y2+….+bmym→min

A11x1+a12x2+…+a1nxn<=b1 a11y1+a21y2+…+am1ym>=c1

A21x1+…+a2nxn<=b2 ……………………………….

…………………… a1ny1+a2ny2+…+amnym>=cn

Am1x1+…+amnxn<=bm

Yi>=0

Xj>=0

Симметричность заключается в том, что в обеих задачах переменные неотрицательны и система ограничений является неравенствами.

Сформулируйте правила составления задачи, двойственной к данной задаче линейного программирования с ограничениями — неравенствами.

В общем случае принято называть двойственной задачей для произвольной задачи ЛП с ограничениями-неравенствами такую задачу ЛП, которая получается из данной задачи следующим образом: каждому ограничению-неравенству исходной задачи ставится в соответствие переменная двойственной задачи, принимающая неотрицательные значения; матрица коэффициентов при неизвестных транспонируется; правые части ограничений заменяются коэффициентами целевой функции; меняются направления неравенств, коэффициенты целевой функции заменяются правыми частями ограничений; от максимизации (минимизации) функции цели переходят к минимизации (максимизации). Говорят, что задачи ЛП обра-зуют симметричную пару.

39. Матричная запись пары двойственных задач ЛП (симметричная пара задач с ограничениями-неравенствами и несимметричная пара, где в одной из задач ограничения имеют вид равенств)

Прямая задача: матричная запись:

z = c₁x₁ + c₂x₂ + … + c_nx_n. →max cx→max

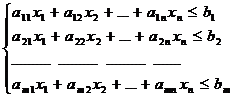Ax≤b

x_j≥0 (j=1,n)

(1)

x_j ³0, j=1,n

Двойственная задача: (симметричная пара – ограничения явл-ся неравенствами и переменные неотрцательные)

F = b₁y₁ + b₂y₂ + … + b_my_m. →min матричная запись:

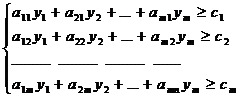yb →min

yA≥c

(1) y_i≥0,(i=1,m)

y_i ³0, i=1,m

Прямая задача: Матричная запись:

z = c₁x₁ + c₂x₂ + … + c_nx_n. →max cx→max

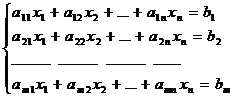Ax=b

x_j≥0 (j=1,n)

(1)

x_j ³0, j=1,n

Двойственная задача (несимметричная): матричная запись:

F = b₁y₁ + b₂y₂ + … + b_my_m. →min yb →min

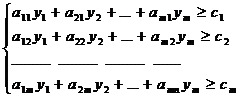yA≥c

y_i – любое число (i=1,m)

(1)