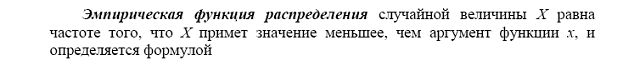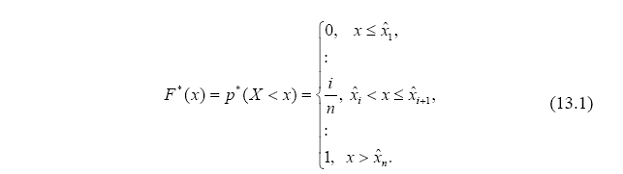Доказать локальную предельную теорему Муавра-Лапласа.

Локальная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р(0<p<1), событие наступит ровно k раз (безразлично, в какой последовательности), приближенно равна (тем точнее, чем больше n). Pn(k)=1/(корень из npq)*фи(х). Здесь Фи(х)=1/(корень из 2пи)*е в степени –х*2/2, x=k – np/(корень из npq). Интегральная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р(0<p<1), событие наступит не меньше k1 раз и не более k2 раз, приближенно равна: P(k1;k2)=Ф(х’’) – Ф(х’). Здесь Ф(х)=1/(корень из 2пи) * интеграл от0 до х е в степени –(z*2/2)dz – функция Лапласа, х’=(k1 – np)/(корень из npq), х’’=(k2 – np)/(корень из npq).

Доказать интегральную предельную теорему Муавра-Лапласа.

Пусть 0< p <1, тогда для схемы Бернулли при n 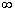 для любых a и b справедлива формула

.

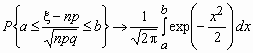Отсюда, в частности, следует, что для вычисления вероятности того, что число успехов в n испытаниях Бернулли заключено между k₁ и k₂, можно использовать формулу

,

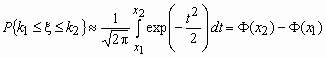где 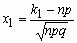, , 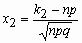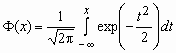- функция Лапласа.

Точность этой приближенной формулы растет с ростом n.

Если npq сравнительно невелико, то лучшее приближение дает формула

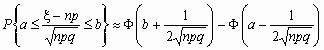
и для вычисления вероятности того, что число успехов в n испытаниях Бернулли заключено между k₁ и k₂, можно использовать формулу

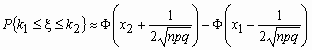, где , .

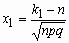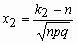Доказать теорему Бернулли о сходимости относительной частоты появления события к вероятности этого события.

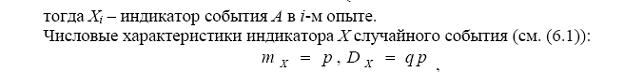
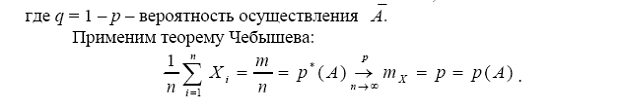
Доказать неравенство Чебышева.

Если случайная величина Х имеет математическое ожидание и дисперсию, то для любого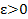

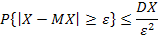
Докажем это неравенство для абсолютно непрерывной случайной величины. Для дискретных случайных величин доказательство проводится аналогично, только интегралы заменяются соответствующими суммами.

Обозначим МХ = а, имеем:

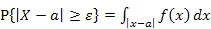(1)

Область интегрирования 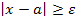можно записать в эквивалентной форме 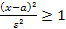, поэтому в этой области 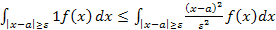,(2)

Последний интеграл с неотрицательной подынтегральной функцией может только возрасти, если расширить область интегрирования до всей прямой:

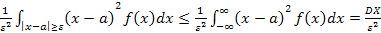(3)

Собирая последовательно равенство (1) и неравенства (2),(3), получаем неравенство Чебышева.

Доказать теорему Чебышева.

Если независимые случайные величины 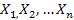имеют математические ожидания 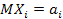и ограниченные в совокупности дисперсии 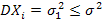, то разность средних арифметических случайных величин и средних их математических ожиданий сходится по вероятности к нулю: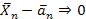

В самом деле, применим неравенство Чебышева к случайной величине 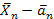. Поскольку

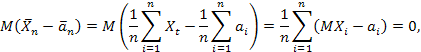
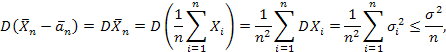
то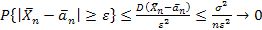

Следовательно,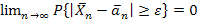

таким образом, действительно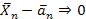

Понятие генеральной совокупности, выборки из нее. Представление выборки в виде вариационного ряда. Определение вариационного ряда.

Эмпирическая функция распределения, ее свойства, способ построения по выборке.