Ускорение точки. Равномерное и равнопеременное движение точки

При естественном способе задания движения ускорение точки определяют формулой

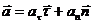. (16)

При этом

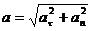, (17)

Где

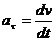, (18)

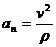. (19)

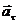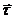a_τ - проекция ускорения на , a 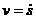- алгебраическая

скорость точки;

a_n - модуль нормального ускорения точки;

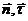-единичные векторы главной нормали и касательной.

Если точка движется равномерно, то

v = const; a_τ = 0; s = s₀ + vt. (20)

При равнопеременном движении a_τ = const. В этом случае

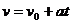, (21)

s = s₀ + v₀ t + 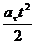, (22)

а также

s = s₀ + 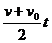, (23)

s = s₀ + 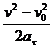. (24)

Пример 4. При прямолинейном движении судна его скорость в пункте А была 10 узлов, а в пункте В стала 30 узлов. Расстояние между пунктами A и В равно 2 милям. Считая в первом приближении движение судна равноускоренным, определить время t движения судна на данном расстоянии, а также модуль его ускорения (узел - 1 единица скорости, равная миле в час, или 0,5144 м/с).

Решение. Если взять начало отсчета в начальном положении судна, то

s₀ = 0; v₀ = 10 узлов; v = 30 узлов; s = 2 мили.

По формуле (23) найдем

t = 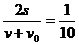ч = 6 мин.

Пользуясь (21), получим

а_τ = 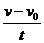= 220узл/ч

Так как движение прямолинейное, то а_τ = а.

Задачи

1.2.8.* Искусственный спутник обращается вокруг Земли на высоте 500 км по круговой орбите. Определить время обращения и модуль скорости спутника, если известно, что его центростремительное ускорение должно быть равно ускорению свободно падающего тела. На данной высоте g = 8,5 м/с², а радиус Земли R ≈ 6370 км.

Ответ: v = 7,64 км/с, t = 1,56 ч.

1.2.9.* Считая движение снаряда в канале ствола равноускоренным, определить изменение модуля скорости снаряда при выходе из канала, если ствол укоротить в п раз.

Ответ: Уменьшится в √п раз.

1.2.10.* Ракета, движущаяся вертикально вверх равноускоренно, в момент окончания процесса горения рабочего вещества (активный участок траектории) достигла высоты 30 км со скоростью 7200 км/ч. Считая дальнейшее движение ракеты равнозамедленным с ускорением, равным по модулю 9,2 м/с², определить время t и полную высоту Н подъема ракеты, если в начальный момент ее скорость была равна нулю.

Ответ: Н = 247 км; t = 4 мин 7с.

1.2.11.* Точка движется по окружности радиусом R равноускоренно из состояния покоя и совершает первый полный оборот за t (с). Определить модули скорости и ускорения точки в конце этого промежутка времени.

Ответ: v = ; .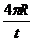

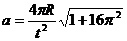Радиус кривизны траектории точки

Радиус кривизны траектории движущейся точки опре­деляют по формуле

.

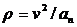Если даны уравнения движения точки в координатной форме: x = x(t); y = y(t); z = z(t), то для определения ρ находят:

1) ; ; ; ;

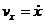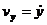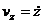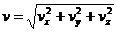2) ;

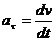3) ; ; ; ;

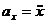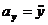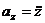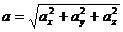4) ;

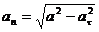5) .

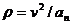Пример 5. Движение точки задано уравнениями

х = b(3cos t + cos 3t),

у = b(3sin t+sin 3t)(b - постоянная величина).

Определить радиус кривизны траектории как функцию времени в промежутке .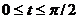

Решение. Определим проекции скорости точки на координатные оси:

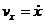= 3b(sin t + sin 3t);

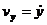= 3b(cos t + cos 3t),

следовательно,

v₂ = 18b² (1 + cos 2t) = 36b² cos² t,

откуда v = 6b cos t.

Касательное ускорение

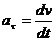= - 6b sin t.

Найдем проекции ускорения точки на координатныеоси:

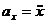= - Зb (cos t + 3 cos 3t);

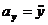= 3b(sin t -3sin 3t),

отсюда

a² = 18b²(5 + З cos 2t).

Определим нормальное ускорение точки:

,

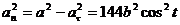откуда

a_n = 126 cos t.

Искомый радиус кривизны траектории

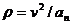= 3bcost.

Наибольший радиус кривизны ρ_mах = 3b.

Пример 6. Точка движется в плоскостихОу с постоянным ускорением 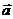, равным по модулю 2 м/с² и направленным параллельно оси Ох. Определить радиус кривизны траектории точки в момент t = 1 с, если в начальный момент точка имела скорость 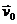равную по модулю 2 м/с и направленную под углом α = 30° к оси Оу.

Решение. Согласно условиям задачи, ускорение 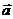постояннопомодулю и направлению. Поэтому в любой момент времени будут иметь место соотношения

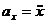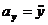= 2; = 0.

Интегрируя, получим

.

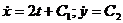Так как при t = 0

; ,

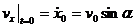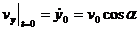то

C₁= v₀ sin α = 1; C₂ = v₀cos α = √3.

Следовательно,

v_х = 2t + 1; v_y = √3.

Теперь найдем модули скорости

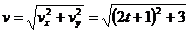
и касательного ускорения

.

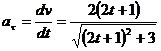В момент t = 1 с, получим

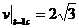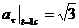м/c; м/с².

Так как a = 2 м/с², то при t = 1 с

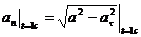= 1 м/с².

После этого найде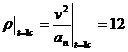м

м.

Задачи

1.2.12.* Движение точки задано уравнениями х = 3t; y = 4t - 3t² (х, у - в сантиметрах, t - в секундах). Определить радиус кривизны траектории точки в те мо­менты, когда она пересекает ось Ох.

Ответ: ρ = 6,94 см.

1.2.13.* Движение точки в вертикальной плоскости задано уравнениями

х = v₀t – r sin 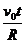; y = R – r cos 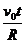, где v₀, r и R — постоянные величины. Определить радиус кривизны траектории точки в наивысшем ее положении.

Ответ: ρ = (r + R)²/r.

1.2.14.* Движение точки задано уравнениями

х = r cos ωt +l sin 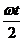; y = - l cos 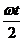+ r sin ωt,

где r, l, ω — постоянные величины.

Определить радиус кривизны траек­тории точки в момент t = π/ω.

Ответ: ρ = .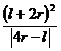

1.2.15.* Движение точки задано уравнениями x = 2b cos t – b cos 2t, y = 2b sin t – b sin 2t, где b - постоян­ная величина. Определить наибольший радиус кривизны траектории точки.

Ответ: ρ_тах = 8b/3

1.2.16.* Движение точки задано уравнениями х = t; y = sin t². Определить радиус кривизны траектории точки в ближайший после начала движения момент вре­мени, в который точка пересекает ось Ох.

Ответ: ρ = 25,1.

1.2.17.* Движение точки задано уравнениями

x= t cos t, y = t sin t, z = Н - 2t, где постоянная величина Н и х, у, z - в метрах, t - в секундах. Определить радиус кривизны траектории точки в момент t = 2 с.

Ответ: ρ = 3,27 м.

1.2.18.* Движение точки задано уравнениями

х = е^t соs t; y = e^t sin t; z = e^t. Определить радиус кривизны траектории точки в момент t.

Ответ: ρ = .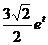

1.2.19.* Точка движется в пространстве с постоян­ным ускорением 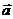, направленным параллельно оси Ох и равным по модулю 5 м/с². В начальный момент точка имела скорость 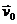равную по модулю 5 м/с и образующую с осями Ох и Оу соответственно углы α = 60° и β = 45°. Определить радиус кривизны траектории точки в момент t = 1 с.

Ответ: ρ = 30 м.

1.2.20.* Угол поворота винта судна диаметром 120 см изменяется по закону φ = 10πt рад (t - в секун­дах). Судно движется прямым курсом с постоянной ско­ростью, равной 10 м/с. Определить радиус кривизны траектории точки винта, наиболее удаленной от оси.

Ответ: ρ = 0,77 м.

1.2.21.*Колесо радиусом R катится без скольже­ния по прямолинейному рельсу со скоростью центра 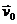= const. Определить радиус кривизны траектории точки на ободе колеса в тот момент, когда оно сделает 1/4 обо­рота, если в начальный момент данная точка совпадала с точкой касания.

Ответ: ρ = 2R√2.

1.2.22.* Из условий задачи 38 определить радиус кривизны траектории точки при повороте колеса на угол 120°.

Ответ: ρ = 2R√3.

1.2.23.*Движение точки по кривой у = х² задано уравнением s = l,5t² - 4t (х, у, s - в метрах, t - в секун­дах). При t = 0 x = y = 0. Определить: 1) характер дви­жения точки в моменты t₀ = 0; t₁ = 1 с и t₂ = 2 с; 2) мо­дули скорости, касательного и нормального ускорений точки в момент t = 0.

Ответ: 1) при t = 0 и t = 1 с движение замедленное, при t = 2 с - ускоренное;

2) v = 4 м/с; a_τ= 3 м/с²; а_n = 32 м/с².

1.2.24.* Движение точки задано уравнениями х = t; y = t²(х, у - в метрах, t - в секундах). Определить модули скорости и ускорения точки, а также радиус кри­визны траектории в момент, когда последний достигает своего наименьшего значения.

Ответ: v = 1 м/с; а = 2 м/с²; ρ = 0,5 м.

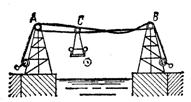1.2.25.* Перемещение грузов по под­весному тросу осуществляется с помощью люльки (рис. 21), под­вешенной к подвижному ролику С. Точки A и В крепле­ния троса находятся на одной горизонтали на

Рис. 21 расстоянии АВ = 40 м.

Считая части троса АС и ВС прямолиней­ными, определить радиус кривизны траектории ролика С, если наибольшее провисание троса равно 4 м. Найти также нормальное ускорение ролика и тот момент, когда он проходит середину троса со скоростью 3 м/с. Разме­рами ролика пренебречь.

Ответ: ρ = 100 м; а_п= 0,0865 м/с²

1.2.26. Даны нормальное а_п = 2,5 м/с² и касательное а_τ = 1,5 м/с² уско­рения точки. Определить полное ускорение точки. (2,92)

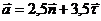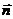1.2.27. Определить модуль ускорения точки, если его вектор , где и 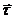- орты естественного триэдра. (4,30)

1.2.28. Точка движется по криволинейной траектории с касательным ус­корением а_τ = 1,4 м/с². Определить нормальное ускорение точки в момент времени, когда ее полное ускорение а = 2,6 м/с². (2,19)

1.2.29. Определить нормальное ускорение точки в момент времени, ког­да ускорение точки а = 1,5 м/с², а угол между векторами ускорения и скорости равен 65°. (1,36)

1.2.30. Точка движется по окружности. Определить радиус окружности, если в момент времени, когда скорость r = 10 м/с, вектор ускорения и вектор скорости, равный по модулю 1,2 м/с, образуют угол 30 . (167)

1.2.31. Ускорение точки равно а = 1 м/с. Векторы ускорения и скорости обра­зуют угол 45°. Определить скорость в км/ч, если радиус кривизны траектории ρ = 300 м. (52,4)

1.2.32. Точка движется по окружности, радиус которой r = 200 м, с касательным ускорением 2 м/с². Определить угол в градусах между векторами скорости и полного ускорения точки в момент времени, когда ее скорость v = 10 м/с. (14,0)

1.2.33. Точка движется по окружности, радиус которой r = 50 м, со скоростью v = 2t. Определить модуль полного ускорения в момент времени t = 5 с. (2,83)

1.2.34. Задано уравнение движения точки по криволинейной траекто­рии: s = 0,2 t² + 0,3t. Определить полное ускорение точки в момент времени t = 3 с, если в этот момент радиус кривизны траектории ρ = 1,5м. (1,55)

1.2.35. Определить скорость точки в момент времени, когда радиус кривизны траектории ρ = 5 м, касательное ускорение а_τ = 2 м/с² , tg β = 3, где β - угол между векторами скорости и ускорения точки (5,48)

1.2.37. По окружности радиуса r = 6 м движется точка со скоростью v = 3t. Определить угол в градусах между ускорением и скоростью точки в момент времени t = 1 с. (26,6)

1.2.37. Точка движется по окружности радиуса r = 9 м. Определить скорость точки в момент времени, когда касательное ускорение а_τ = 2 м/с², а вектор полного ускорения 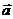образует угол 70° с касательной к траектории. (7,03)

1.2.38. Точка движется по окружности радиуса r = 200 м из состояния покоя с постоянным касательным ускорением а_τ = 1 м/с². Опреде­лить, полное ускорение точки в момент времени t = 20с. (2,24)

1.2.39. На рис. 22 приведены графики ускорений

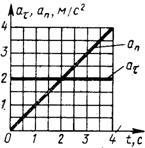а_τ = а_τ (t) и а_п = а_п (t). Определить, какой угол в градусах образует полное ускорение с направлением скорости в момент времени t = 3 с. (56,3)

1.2.40. Точка движется по окружности радиуса r = 2 м. Нормальное ускорение точки

меняется согласно закону а_n= 2t².

Рис. 22 Определить угол в градусах между векторами скорости и полного ускорения точки в момент времени t = 1 с. (45)

1.2.41. Задан закон движения точки по траектории: s = 0,5t². Опреде­лить угол в градусах между векторами скорости и полного ускорения точки в момент времени t₁= 3 с, когда радиус кривизны ρ = 4 м.(66,0)

1.2.42. По окружности радиуса r = 1 м движется точка согласно урав­нению s = 0,1 t³. Определить полное ускорение точки в момент вре­мени t = 2 с. (1,87)

1.2.43. Точка движется по криволинейной траектории с касательным ускорением а_τ = 2 м/с². Определить угол в градусах между векторами скорости и полного ускорения точки в момент времени t₁= 2 с, когда радиус кривизны ρ = 4 м, если при t₀ = 0 скорость v₀ = 0. (63,4)