Уравнение движения точки по траектории. Скорость точки
КИНЕМАТИКА
1.1. КООРДИНАТНЫЙ И ВЕКТОРНЫЙ СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ 
1.1.1. Уравнения движения точки в декартовых координатах. Траектория
При координатном способе задания движения положение точки в пространстве в любой момент времени t определяется декартовыми координатами
х = x(t); y = y(t); z = z(t). (1)
Уравнения (1) называют уравнениями движения точки в координатной форме. При векторном способе задания движения положения точки в любой момент времени определяется ее радиус-вектором:
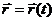 . (2)
. (2)
Исключив из уравнений (1) параметр t, получим уравнения кривой, по которой движется точка в явном виде. Траекторией точки может быть вся полученная кривая или ее часть. Для определения траектории следует установить области изменения координат х, у и z по заданным уравнениям движения, считая время движения t положительной величиной. При известном уравнении кривой, по которой движется точка, траектория во многих случаях может быть выделена заданием области изменения только одной координаты. При исследовании траекторий точек механизмов следует учитывать также конструктивные особенности данного механизма, ограничивающие его движение.
Пример 1.Движениеточки в плоскости хОу (рис.1) задано уравнениями: х = a sint, y = 2a cos 2t,где а - постоянная (а > 0). Определить траекторию точки и исследовать ее движение.
Решение. Заданные уравнения движения точки являются уравнениями траектории в параметрической форме.Для получения уравнения траектории в явном виде точка, следуетиз этих уравнений исключить параметр t.
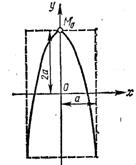 у = 2а cos 2t = 2a (1 — 2 sin2 t).
у = 2а cos 2t = 2a (1 — 2 sin2 t).
Из первого уравнения движения точки находим sin t = х/а, тогда
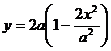 .
.
Это уравнение параболы, вершина которой находится в точке (0, 2а), а ветви направлены вниз. Однако не вся полученная парабола является траек-торией точки. Действительно, |х| ≤ а,
Рис. 1 |у| ≤ 2а, т. е. траекторией точки является часть параболы, заключенная внутри прямоугольника со сторонами 2a и 4а. Таким образом, уравнением траектории точки является
у = 2а 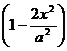 при – а ≤ х ≤ а.
при – а ≤ х ≤ а.
Найдем начальное положение точки. При t = 0
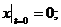
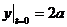 ,
,
т. е. точка в начальный момент находилась в вершине параболы. При возрастании t от 0 до π/2, абсцисса х увеличивается, а ордината у уменьшается, т. е. точка движется по параболе вправо. При t = t1 = π/2 с
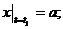
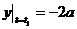 .
.
В промежутке π/2 ≤ t ≤ 3π/2 с точка движется по параболе влево, проходя ее вершину в момент t = t2 = π с. Начиная с момента t = t3 = 3π/2 с, точка снова движется вправо, проходя начальное положение в момент t = t4 = 2π с, и т.д. Таким образом, точка совершает с течением времени колебательное движение вдоль параболы.
Пример 2. Зубчатое колесо Ι радиусом r (рис. 2) обкатывается внутри неподвижного зубчатого колесаIIрадиусом R = 2r с помощью кривошипа О1О2 угол поворота которого φ задан как функция времени: φ = kt (k - постоянная). Определить уравнения движения и траекторию конца А отрезка АВ длиной l, неизменно связанного с колесом I и расположенного вдоль его радиуса. При t = 0 колесо I занима-ло нижнее положение (показанное на рисунке пунктиром) и точка В совпадала с центром колесаII.
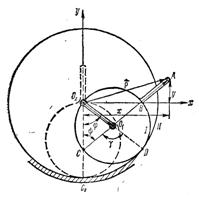 Решение. Рассмотрим положение механизма в некоторый текущий момент времени t. Колесо I займет при этом положение, показанное на рисунке.
Решение. Рассмотрим положение механизма в некоторый текущий момент времени t. Колесо I займет при этом положение, показанное на рисунке.
Пусть С - точка колеса I, которая в начальный момент t = 0 находилась в С0 - месте зацепления колес. Из условия отсутствия скольжения (благодаря наличию зубцов)
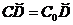 или
или
Rφ = rγ, где γ = 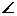 CO1D.
CO1D.
Имея в виду, что R = 2r, получим γ = 2φ. Обозначим
Рис.2 через ψ острый угол, состав-ленный диаметром СB с вертикальной осью О2у. По теореме о внешнем угле треугольника γ = φ + ψ = 2φ, откуда ψ = φ.
Отсюда легко заключить, что точка С в процессе всего движения перемещается вдоль оси О2у.
Обозначим координаты точки А через х и у. Введем радиус-вектор 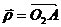 .Из рисунка видно, что
.Из рисунка видно, что
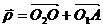 .
.
Проектируя это векторное равенство на оси, получим:
х = O2O1 sin φ + O1A sin ψ = (2r + l) sin φ,
у = - O2О1 cos φ + O1A cos ψ = l cos φ.
Отсюда следует, что точка В в процессе движения перемещается вдоль оси О2х, так как уВ = уА – l соs φ=0.
Подставляя φ = kt, получим уравнения движения точки А:
х = (2r + l) sin kt, y = l cos kt,
которые одновременно являются и уравнениями траектории точки в параметрической форме. Исключая время t, получим уравнение кривой, по которой движется точка, в непараметрической форме.
Для исключения t перепишем уравнения движения в виде
х/(2r + l) = sin kt; y/l = cos kt.
Пользуясь тождеством sin2 kt+cos2 kt =1, получим
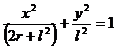 . (а)
. (а)
Это эллипс с полуосями а =2r + l, b = l и центром в начале координат. При изменении t от 0 до ∞ абсцисса х изменяется в пределах –a ≤ x ≤ a, а ордината у - в пределах –b ≤ y≤ b, и, следовательно, точка в своем движении обходит весь эллипс. Таким образом, в данной задаче вся кривая, определяемая уравнением (а), является траекторией точки.
Задачи
1.1.1.* По заданным в векторной форме уравнениям движения точки определить ее траекторию:
 1)
1) 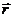 = (2t+1)
= (2t+1)  +(2-3t)
+(2-3t) 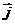 ;
;
2) 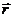 = (2+3t)
= (2+3t) 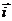 +(1-2t)
+(1-2t) 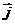 +(2+t)
+(2+t) 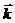 ;
;
3) 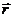 = t2
= t2 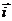 +(5-2t2)
+(5-2t2) 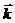 ;
;
4) 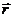 = 3 cos
= 3 cos 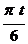
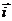 +
+ 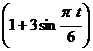
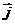 ;
;
5) 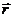 = (2+sin
= (2+sin 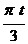 )
) 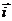 +(l+2cos
+(l+2cos 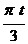 )
) 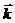 ;
;
6) 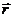 = 6cos2t
= 6cos2t 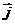 +t
+t 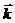 ;
;
7) 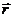 = (3 + 2 cos 2t)
= (3 + 2 cos 2t) 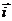 + (2 -3 sin 2t)
+ (2 -3 sin 2t) 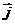 ;
;
8) 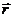 =3 sin t3+2 cos t3
=3 sin t3+2 cos t3 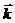 ;
;
9) 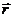 = t
= t 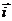 +(2t - t2)
+(2t - t2) 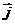 ;
;
10) 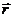 = cos 2t
= cos 2t 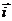 +sin t
+sin t 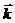 .
.
Ответы:
1) Зх + 2у = 7; z = 0 (l ≤ x ≤  );
);
2) 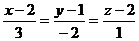 (2≤ х ≤
(2≤ х ≤  );
);
3) 2 х + z = 5;y = 0(0≤ x ≤  );
);
4) х2 + (y - l)2 = 9; z = 0;
5) (х - 2)2 + (z -1)2/4 = 1; y = 0;
6) y = 6 cos 2z; x = 0 (0 ≤ z ≤ 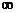 );
);
7) 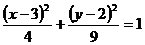 ; z = 0;
; z = 0;
8) y2/9 + z2/4 = 1; x = 0;
9) y = 2x - x2; z = 0 (0 ≤ x < 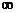 );
);
10) x = l - 2z2; y = 0 (-l ≤ x ≤ l).
1.1.2.* По заданным уравнениям движения точки найти ее траекторию в плоскости хОу и начальное положение:
1) x = 2sin 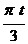 ; y = 3cos
; y = 3cos 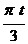 ;
;
2) x =3cos t; y =3 -5sin t;
3) x = 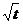 ; y = e-t;
; y = e-t;
4) x = t3 + 2; y = 3 - t3;
5) x = 2 cos 2t; y =3 sin t;
6) x = 4 sin 2t; y =2 cos t;
7) x = 2 tg 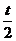 ; y = 3 sin t (t< π);
; y = 3 sin t (t< π);
8) x = 3 tg 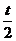 ; у = соs t (t < π);
; у = соs t (t < π);
9) x = 3t; y = 6t - 5t2;
10) x = a(sin kt + cos kt); y = b(sin kt – cos kt); 
11) x = 2sin t2; y = 3cos t2;
12) x = a + r cos ωt; y= r sin ωt.
Ответы:
1) x2/4 + y2/9 = 1. При t = 0: x0 = 0; y0 = 3;
2) 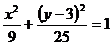 . При t = 0: x0 = 3; y0 = 3;
. При t = 0: x0 = 3; y0 = 3;
3) у = е-х (0≤ x < 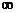 ). При t = 0: x0 = 0; y0 = 1;
). При t = 0: x0 = 0; y0 = 1;
4) x + y = 5 (2≤ x < 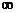 ). При t = 0: x0 = 2; y0 = 3;
). При t = 0: x0 = 2; y0 = 3;
5) y2 = 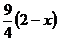 (- 2≤ x ≤2). При t = 0: x0 = 2; y0 = 1;
(- 2≤ x ≤2). При t = 0: x0 = 2; y0 = 1;
6) x2 = 4y2(4 - y2) (- 4 ≤ x≤ 4 ). При t = 0: x0 = 0; y0 = 2;
7) y = 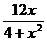 (0 ≤ x<
(0 ≤ x<  ). При t = 0: x0 = 0; y0 = 0;
). При t = 0: x0 = 0; y0 = 0;
8) y = 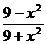 (0 ≤ x<
(0 ≤ x< 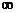 ). При t = 0: x0 = 0; y0 = 1;
). При t = 0: x0 = 0; y0 = 1;
9) y = 2x- 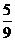 x2 (0 ≤ x<
x2 (0 ≤ x< 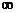 ). При t = 0: x0 = 0; y0 = 0;
). При t = 0: x0 = 0; y0 = 0;
10) 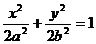 . При t = 0: x0 = a; y0 = - b;
. При t = 0: x0 = a; y0 = - b;
11) 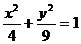 . При t = 0: x0 = 0; y0 = 3;
. При t = 0: x0 = 0; y0 = 3;
12) (х - а)2 + y2 = r2. При t = 0: x0 = a + r; y0 = 0.
1.1.3.* Точка движется по окружности радиусa r против хода часовой стрелки так, что проходимая ею дуга изменяется по закону s = kt. Найти уравнения движения точки по отношению к системе хОу с началом в центре окружности, если горизонтальная ось Ох проходит через начальное положениеточки.
Ответ: x = r cos 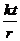 ; у = r sin
; у = r sin 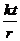 .
.
1.1.4.* Кулиса ОМ длиной l приводится вдвижение кривошипом ОА (рис. 3), вращающимся по закону φ = kt2. Составить уравнения движения конца кулисы М, если O1O = O1A.
Ответ: x= l sin 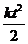 ; у = l cos
; у = l cos 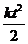 .
.
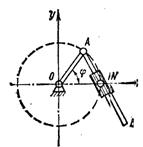
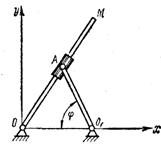
Рис.3Рис. 4
1.1.5.* Стержень АВ длиной l движется так (рис. 4), что одна из его точек описывает окружность радиусом r = l/2, а сам стержень проходит через неподвижную точку N, лежащую на той же окружности. Составить уравнения движения точки В, если φ = ωt.
Ответ: х = r cos ωt + l sin 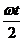 ; у = r sin ωt – l cos
; у = r sin ωt – l cos 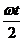 .
.
1.1.6.* В V-образном двигателе угол между осями цилиндр α =90° (рис. 5). Коленчатый вал вращается по закону φ = ωt. Составить уравнения движения пальцев В и С, если длина кривошипа. ОА = R, а длины шатунов АВ и АС равны L.
Ответ: 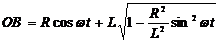 ;
;
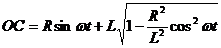 .
.
1.1.7.*В V-образном двигателе (рис.5) угол а между осями цилиндров равен 60°. Коленчатый вал вращается по закону φ = ωt. Составить уравнения движения пальцев В и С по направляющим, если длина кривошипа ОА равна R. А длины шатунов АВ и АС равны2R. Определить положение пальца поршня В в тот момент, когда поршень С находится в крайнем верхнем положении.
Ответ: 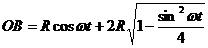 ;
;
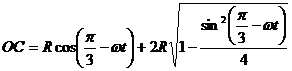 ;
;
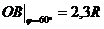 .
.
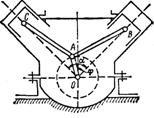
Рис.5 Рис. 6
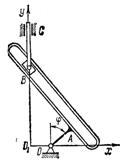 1.1.8.*Стержень АВ длиной l поворачивается около точки В (рис.6)так, что угол φ изменяется по закону φ = ωt, а ползун В совершает гармонические колебания согласно уравнению s = a + b sin ωt. Определить траекторию точки А.
1.1.8.*Стержень АВ длиной l поворачивается около точки В (рис.6)так, что угол φ изменяется по закону φ = ωt, а ползун В совершает гармонические колебания согласно уравнению s = a + b sin ωt. Определить траекторию точки А.
Ответ: (х - а)2/(b + l)2+(у2/ l2) =1 (эллипс).
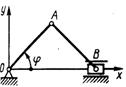
1.1.9.*В механизме (рис. 7) найти уравнение движения точкиВ, если кулиса ОАВ вращается так, что угол φ = ωt, а расстояние от точки О до направляющей стержня ОО1 = b,
длина ОА равна а. Угол OAВ – прямой.
Рис.7 Ответ: у = 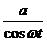 + b tg ωt.
+ b tg ωt.
 1.1.2. Скорость и ускорение точки в декартовых координатах
1.1.2. Скорость и ускорение точки в декартовых координатах
При задании движения точки в прямоугольных декартовых координатах скорость и ускорение точки определяются по их проекциям на неподвижные оси:
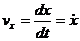 ;
; 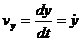 ;
; 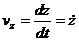 ; (3)
; (3)
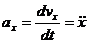 ;
; 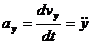 ;
; 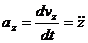 ; (4)
; (4)
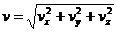 ; (5)
; (5)
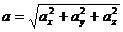 ; (6)
; (6)
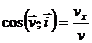 ;
; 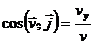 ;
; 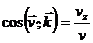 ; (7)
; (7)
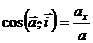 ;
; 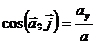 ;
; 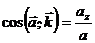 . (8)
. (8)
Уравнения годографа скорости в параметрическом виде:
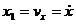 ;
; 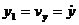 ;
; 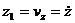 , (9)
, (9)
где х1, у1, z1 - текущие координаты точки, вычерчивающей годограф, а оси О1х1, O1y1, O1z1, соответственно параллельны осям Ох, Оу, Оz.
Пример 3.Даны уравнения движения точки; x = t2; y = t3/3. Определить: траекторию точки, скорость точки в момент t = 1 c, годограф скорости, ускорение точки при t = 2 c.
Решение. 1. Исключаяt из уравнений движения, получим уравнение кривой, по которой движется точка:
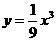
(полукубическая парабола). Траекторией является часть этой параболы, соответствующая x ≥ 0.
2. Находим проекции скорости точки на оси координат по формулам (3)
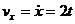 ;
; 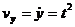 ,
,
откуда 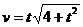 .Следовательно, v |t=l = √5 = 2,24.
.Следовательно, v |t=l = √5 = 2,24.
Направление скорости определяется направляющими косинусами (7):
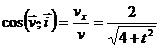 ;
; 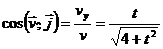 ;
;
При t =1 c
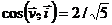 ;
; 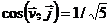 .
.
Таким образом, скорость в момент t = 1 c составляет с осями Ох и Оу соответственно углы 26°34' и 63°26'.
3. Находим уравнения годографа скорости в параметричес-ком виде по формулам (9): 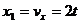 ;
; 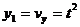 .
.
Исключая t, получим 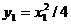 .
.
Годографом скорости точки является часть этой параболы, соответствующая (0 ≤ x1< 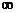 ).
).
4. Находим проекции ускорения точки на оси координат по формулам (4):
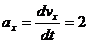 ;
; 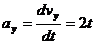 .
.
Отсюда 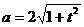 , следовательно,
, следовательно,
a│t=2 = 2√5 = 4,47.
Направление ускорения определяется направляющими косинусами по формулам (8):
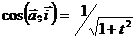 ;
; 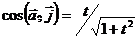 .
.
При t = 2 получим 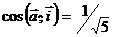 ;
; 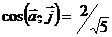 .
.
Таким образом, вектор 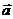 в моментt = 2 образует с осямиОх и Оу соответственно углы 63°26 и 26°34'.
в моментt = 2 образует с осямиОх и Оу соответственно углы 63°26 и 26°34'.
Пример 4. Груз С поднимается по вертикальной направляющей с помощью троса, перекинутого через неподвижный блок А (рис. 8)., отстоящий от направляющей на расстоянии АО = b. Определить скорость и ускорение груза С в 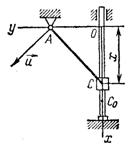 зависимости от расстоянияОС = х, если свободный конец троса тянут с постоянной скоростью и.
зависимости от расстоянияОС = х, если свободный конец троса тянут с постоянной скоростью и.
Решение. Из треугольника АОС 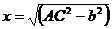 .
.
Пусть С0 - начальное положение груза. Обозначая АС0= l, получим AC = l – ut,и уравнение движения груза С примет вид
Рис. 8 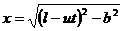 .
.
Находим проекцию скорости на ось Ох:
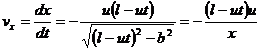 .
.
Из уравнения движения груза находим
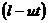 =
= 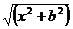 ,
,
следовательно 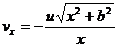 .
.
Знак минус указывает на то, что точка движется в сторону уменьшения абсциссы х, т. е. вверх.
Находим проекцию ускорения точки на ось Ох:
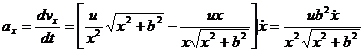 .
.
Так как 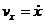 , то окончательно получим
, то окончательно получим
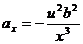 .
.
Знак минус указывает на то, что ускорение точки направлено также вверх таким образом, движение груза ускоренное.
Задачи
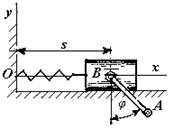
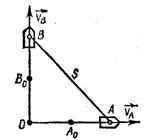 1.1.10.* Два судна А и В идут взаимно перпендикулярными курсами (рис. 9) с постоянными скоростями, равными по модулю 20 узлам (узел — единица скорости, равная миле в час). Определить закон изменения расстояния s между ними, если в
1.1.10.* Два судна А и В идут взаимно перпендикулярными курсами (рис. 9) с постоянными скоростями, равными по модулю 20 узлам (узел — единица скорости, равная миле в час). Определить закон изменения расстояния s между ними, если в
Рис. 9 начальный момент суда занимали положения А0 и B0, причем ОА0 = ОВ0 = 3 мили.
Ответ: s = √2 (3 + 20t) миль (t- в часах).
1.1.11. Дано уравнение движения точки 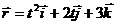 .Определить модуль скорости точки в момент времени t = 2 с. (4,47)
.Определить модуль скорости точки в момент времени t = 2 с. (4,47)
1.1.12. Дан график скорости движения точки (рис.10) 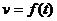 . Определить пройденный путь в момент времени t = 5 с. (7,5)
. Определить пройденный путь в момент времени t = 5 с. (7,5)
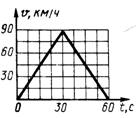
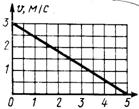
Рис. 10 Рис. 11
 1.1.13. Дан график скорости движения точки v = f(t) (рис.11).Определить пройденный путь в момент времени t = 60 с. (750)
1.1.13. Дан график скорости движения точки v = f(t) (рис.11).Определить пройденный путь в момент времени t = 60 с. (750)
1.1.14. Положение кривошипа (рис.12) определяется углом φ = 0,5t.
Рис. 12 Определить скорость ползуна В в момент времени t = 4 с, если ОА = АВ = 1,5 м. (-1,36)
1.1.15. Даны уравнения движения точки х = t2, у = sin πt, z = cos πt. Определить модуль скорости точки в момент времени t = 1 с. (3,72)
1.1.16. Скорость движения точки 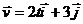 . Определить угол в градусах между вектором скорости и осью Ох в момент времени t = 4 с. (20,6)
. Определить угол в градусах между вектором скорости и осью Ох в момент времени t = 4 с. (20,6)
1.1.17.Проекция скорости точки vх = 2 cos πt. Определить координату х точки в момент времени t = 1 с, если при t0 = 0 координата х0 = 0. (0)
1.1.18.Дано уравнение движения точки х = sin πt. Определить скорость в ближайший после начала движения момент времени t, когда координата х = 0,5 м. (2,72)
1.1.19.Заданы уравнения движения точки 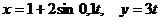 . Определить координату х точки в момент времени, когда ее координата у=12 м. (1,78)
. Определить координату х точки в момент времени, когда ее координата у=12 м. (1,78)
1.1.20.Задано уравнение движения точки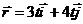 .Определить координату у точки в момент времени, когда r = 5 м. (4)
.Определить координату у точки в момент времени, когда r = 5 м. (4)
1.1.21. Заданы уравнения движения точки 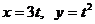 . Определить расстояние точки от начала координат в момент времени t=2 c. (7,21)
. Определить расстояние точки от начала координат в момент времени t=2 c. (7,21)
1.1.22.Скорость автомобиля равномерно увеличивается в течение 12 с от нуля до 60 км/ч. Определить ускорение автомобиля. (1.39)
1.1.23.Сколько секунд должен работать двигатель, который сообщает ракете ускорение 3g, чтобы скорость ракеты в прямолинейном движении возросла с 3 до 5 км/с? (68,0)
1.1.24.Самолет при посадке касается посадочной полосы с горизонтальной скоростью 180 км/ч. После пробега 1000 м самолет останавливается. Определить модуль среднего замедления самолета. (1,25)
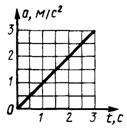 1.1.25. Дан график ускоре-ния а = f(t) прямолинейно движущейся точки (рис. 13). Определить скорость точки в момент времени t = 2 с, если при t0 = 0 скорость v0 = 0. (2)
1.1.25. Дан график ускоре-ния а = f(t) прямолинейно движущейся точки (рис. 13). Определить скорость точки в момент времени t = 2 с, если при t0 = 0 скорость v0 = 0. (2)
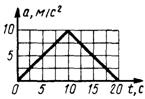 Рис.13 1.1.26. Дан график ускорения а = f(t) прямолинейно движущейся точки (рис.14). Определить скорость точки в момент времени t = 20 с, если при t0= 0 скорость v0= 0. (100)
Рис.13 1.1.26. Дан график ускорения а = f(t) прямолинейно движущейся точки (рис.14). Определить скорость точки в момент времени t = 20 с, если при t0= 0 скорость v0= 0. (100)
Рис. 14
1.1.27. Скорость автомобиля 90 км/ч. Определить путь торможения до остановки, если среднее замедление автомобиля равно 3 м/с см, а закон изменения угла φ = 3t. (104)
1.1.28.Ускорение точки 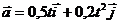 . Определить модуль ускорения в момент времени t = 2 с. (1,28)
. Определить модуль ускорения в момент времени t = 2 с. (1,28)
1.1.29. Скорость точки 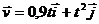 . Определить модуль ускорения точки в момент времени t = 1,5 с. (3,13)
. Определить модуль ускорения точки в момент времени t = 1,5 с. (3,13)
1.1.30. Определить ускорение точки В (рис.15) в момент времени, когда угол φ = 60°, если длина ОА = АВ = 20 (-1,8)
1.1.31. Определить ускорение точки В (рис. 16) в момент времени t =5 с, если длина кривошипа ОА = 15 см, а закон изменения угла φ = 3t. (-2,19)
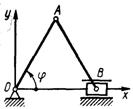
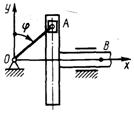
Рис. 15 Рис.16
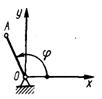 1.1.32.Положение кривошипа ОА (рис.17) определяется углом φ = 2t. Определить проекцию ускорения ах точки А в момент времени t = 1 с, если длина ОА = 1 м. (1,66)
1.1.32.Положение кривошипа ОА (рис.17) определяется углом φ = 2t. Определить проекцию ускорения ах точки А в момент времени t = 1 с, если длина ОА = 1 м. (1,66)
1.1.33. Положение линейки АВ (риc.
18) определяется углом φ = 0,2 t.
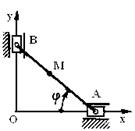 Рис. 17 Определить в см/с2 проекцию ускорения точки M на ось Оу в момент времени t = 3 с, если расстояние AM = 50 см. (-1,13)
Рис. 17 Определить в см/с2 проекцию ускорения точки M на ось Оу в момент времени t = 3 с, если расстояние AM = 50 см. (-1,13)
1.1.34. Движение точки задано уравнениями dx/dt = 0,3t2 и у = 0,2 t3. Определить ускорение в момент времени
t = 7 с. (9,39)
Рис. 18
1.1.35. Даны проекции скорости на координатные оси vx= 3t, vy =2 t2, vz = t3. Определить модуль ускорения в момент времени t = 1 с. (5,83)
1.2. ЕСТЕСТВЕННЫЙ СПОСОБ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
Из рисунка найдем
X = ON cos φ + NM sin φ = R cos φ + Rφ sin φ;
y = - ON sin φ + NM cos φ= - R sin φ - Rφ cos φ.
При сматывании троса угол φ = φ(t), следовательно, эти уравнения являются уравнениями движения точки М.
Найдем проекции скорости точки на выбранные оси:
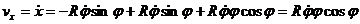 ;
;
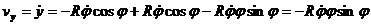 ,
,
следовательно,
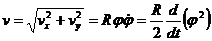 .
.
Считая, что φ = 0, s = 0 при t = 0, по формуле (14) найдем
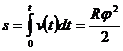 .
.
Если вместо φ подставить известную функцию φ = φ(t), то
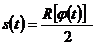 ,
,
т. е. получим уравнение движения точки по траектории.
Пример 2. Движение точки по траектории задано уравнением 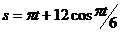 (s - в метрах, t - в секундах). Определить значение дуговой координаты s в момент t = 15 с и путь σ, пройденный точкой за первые 15 с.
(s - в метрах, t - в секундах). Определить значение дуговой координаты s в момент t = 15 с и путь σ, пройденный точкой за первые 15 с.
Решение. Определим скорость точки
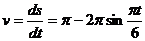 .
.
Найдем моменты времени t1, t2,…, в которые скорость точки изменяет свой знак:
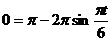 ,
,
откуда tn+1 = (-l)n +6n с (п = 0;1; 2; ...).
Следовательно, в течение первых 15 с скорость изменяет свой знак в моменты времени: t1= l с, t2 = 5 с, t3 = 13 с.
Определим значения дуговой координаты s вэти моменты времени, а также в момент
t0 = 0 и в момент t4 = 15 с:
s0 = 12 м;
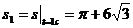 м;
м;
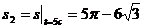 м;
м;
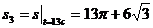 м;
м;
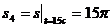 м.
м.
Пользуясь формулой (15), найдем путь, пройденный точкой за первые 15 с:
П = |π+6√З-l2| + |5π-6√3-π-6√3| + |13π+6√3-5π+6√3 | +
+|15π-13π-6√3| = 59,7 м.
Пример 3. Определить уравнение движения точки по траектории, если даны ее уравнения движения в декартовых координатах:
х = а (2 cos t + cos 2t), y = a(2sin t—sin 2t), 0 ≤ t ≤ 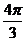 .
.
Дуговую координату отсчитывать от начального положения точки в сторону первоначального движения.
Решение. Заданные уравнения представляют собой параметрические уравнения гипоциклоиды, т. е. линии, которую описывает точка окружности радиусом а, катящейся внутри окружности радиусом 3а, причем t равно углу поворота линии центров от ее начального положения.
Для определения s найдем v(t):
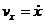 = - 2а (sin t + sin 2t),
= - 2а (sin t + sin 2t),
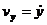 = 2a (cos t - cos 2t),
= 2a (cos t - cos 2t),
отсюда 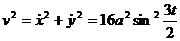 .
.
Заметим, что величина v(t) всегда положительна, так как точка не меняет направления своего движения. Это следует из вышеуказанной интерпретации движения. Аналитически в этом можно убедиться, если рассмотреть изменение угла φ, образованного радиус-вектором точки с осью абсцисс:
tg φ = x/y; φ = arc tg x/y,
отсюда
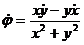
Знаменатель и числитель всегда положительны, так как
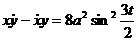 .
.
Таким образом, точка всегда движется в одном направлении (φ растет) и скорость сохраняет постоянный знак, который совпадает с ее первоначальным знаком:
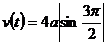 .
.
Для s(t) получим
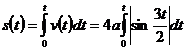 .
.
Этот интеграл не может быть вычислен в элементарных функциях (для произвольного t). Вычислим его по участкам.
При 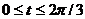
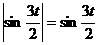 ,
,
тогда s(t)= 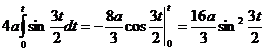 .
.
В частности, при t = 2π/3
s = (2π/3) = 16a/3.
Применять эту формулу при больших t нельзя. Например, при t = 4π/3 она привела бы к нелепому результату s = 0. При 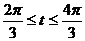 ,
, 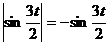 .
.
Тогда
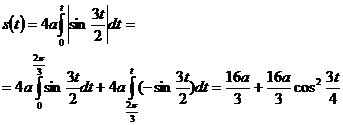 .
.
Задачи
1.2.1.* Определить уравнение движения точки по траектории, а также значение дуговой координаты s и пройденный путь σ к моменту t = 5с, если ее скорость v задана уравнением:
1) v =10 см/с;
2) v = 2 см/с (0 ≤ t ≤ 3);
v = (5 - t) см/с(3 ≤ t ≤ 5);
3) v = (2t+1) см/с;
4) v = (3 - t) см/с;
5) v = 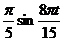 см/с;
см/с;
6) 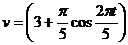 см/с;
см/с;
7) 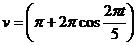 см/с;
см/с;
8) v = (t2 - 3t + 2) см/с.
Ответы:
1) s = 10t см; s|t=5c = 50 см; σ|t=5c = 50 см;
2) s = 2t см (0 ≤ t ≤ 3); s = (5t - 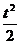 - 4,5) см (3 ≤ t ≤ 5);
- 4,5) см (3 ≤ t ≤ 5);
s|t=5c = 8 см; σ|t=5 c= 8 см;
3) s = (t2 + t) см; s|t=5c = 30 см; σ|t=5c = 30 см;
4) s =(3t - 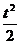 ) см; s|t=5c = 2,5 см; σ|t=5c = 6,5 см;
) см; s|t=5c = 2,5 см; σ|t=5c = 6,5 см;
5) s = 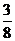 (1- cos
(1- cos 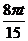 ) см; s|t=5c =
) см; s|t=5c = 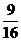 см; σ|t=5c = 2
см; σ|t=5c = 2 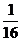 см;
см;
6) s = (3t + 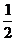 sin
sin 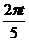 ) см; s|t=5c = 15 см; σ|t=5c = 15см;
) см; s|t=5c = 15 см; σ|t=5c = 15см;
7) s = (πt +5 sin 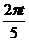 ) см; s|t=5c = 5π см;
) см; s|t=5c = 5π см;
σ|t=5c = 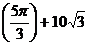 см;
см;
8) s = 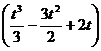 см; s|t=5c =
см; s|t=5c = 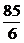 см; σ|t=5c =
см; σ|t=5c = 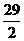 см.
см.
1.2.2.*Определить уравнение движения точкипотраектории, если даны уравнения ее движения в декартовых координатах. Дуговую координату s отсчитывать от начального положения точки в сторону первоначального движения:
1) x = Зt2 + 5; y = 4t2 + 3;
2) x = 1 – t; y = t - 1;
3) x = 2sin 2t; y = 2cos 2t;
4) x = a+r cos ωt; y = r sin ωt;
5 ) х = 3cos t2; y = 3sin t2;
6) 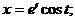
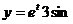 ; z = et;
; z = et;
7) x = 4a cos2ωt; y = За sin2ωt;
8) x = acos3t; y = a sin3t;
9) x = a(t - sin t ); y = a(l - cos t);
10) x = a cos t; у = a sint; z = ct.
Ответы: 1) s = 5t2;
2) s = 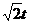
3) s = 4t;
4) s = rωt;
5) s = 3t2;
6) s = √3(et—l);
7) s = 5a sin2ωt;
8) s = 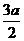 sin2t [
sin2t [ 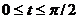 (см. пример 3)];
(см. пример 3)];
9) s = 4a(l-cos 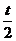 ) [
) [ 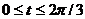 (см. пример 3)];
(см. пример 3)];
10) 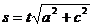 .
.
1.2.3.* Колесо радиусом R катится без скольжения по горизонтальному рельсу со скоростью центра 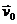 . Определить уравнение движения по траектории точки обода колеса, находившейся в начальный момент в точке касания с рельсом. Какое расстояние si будет пройдено точкой по траектории от начала движения до наивысшего положения?
. Определить уравнение движения по траектории точки обода колеса, находившейся в начальный момент в точке касания с рельсом. Какое расстояние si будет пройдено точкой по траектории от начала движения до наивысшего положения?
Ответ: s = 8R sin2 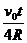 ; si = 4R. Выражение для s справедливо только до момента t =
; si = 4R. Выражение для s справедливо только до момента t = 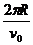 , при котором s = 8R. После него нужно вычислять s так же, как в примере 3.
, при котором s = 8R. После него нужно вычислять s так же, как в примере 3.
1.2.4. Точка движется по траектории согласно уравнению s = 15 + 4 sin πt. Указать ближайший после начала движения момент времени t1, при котором s1=17 м. (0.167)
1.2.5. Точка движется по траектории согласно уравнению s = 0,5t2 + 4t. Определить, в какой момент времени скорость точки достигнет 10 м/с. (6)
1.2.6. Точка движется по заданной траектории со скоростью v = 5 м/с. Определить криволинейную координату s точки в момент времени t = 18 с, если при
t0 = 0 координата s0 = 26 м. (116)
1.2.7. Точка движется по кривой со скоростью v = 0,5 t. Определить ее координату в момент времени t = 10 с, если при t0 = 0 координатa точки s0 = 0. (25)
При этом
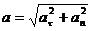 , (17)
, (17)
Где
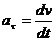 , (18)
, (18)
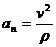 . (19)
. (19)
aτ - проекция ускорения 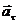 на
на 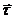 , a
, a 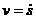 - алгебраическая
- алгебраическая
скорость точки;
an - модуль нормального ускорения точки;
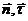 -единичные векторы главной нормали и касательной.
-единичные векторы главной нормали и касательной.
Если точка движется равномерно, то
v = const; aτ = 0; s = s0 + vt. (20)
При равнопеременном движении aτ = const. В этом случае
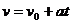 , (21)
, (21)
s = s0 + v0 t + 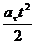 , (22)
, (22)
а также
s = s0 + 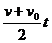 , (23)
, (23)
s = s0 + 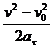 . (24)
. (24)
Пример 4. При прямолинейном движении судна его скорость в пункте А была 10 узлов, а в пункте В стала 30 узлов. Расстояние между пунктами A и В равно 2 милям. Считая в первом приближении движение судна равноускоренным, определить время t движения судна на данном расстоянии, а также модуль его ускорения (узел - 1 единица скорости, равная миле в час, или 0,5144 м/с).
Решение. Если взять начало отсчета в начальном
