Что такое параметрическое линейное программирование?Где может находиться параметр?

Параметрическое программирование представляет собой один из разделов математического программирования, изучающий задачи, в которых целевая функция или ограничения зависят от одного или нескольких параметров.

Необходимость рассмотрения подобных задач обусловлена различными причинами. Одной из основных является та, что исходные данные для численного решения любой реальной задачи оптимизации в большинстве случаев определяются приближенно или могут изменяться под влиянием каких-то факторов, что может существенно сказаться на оптимальности выбираемой программы (плана) действий. Соответственно, разумно указывать не конкретные данные, а диапазон возможного изменения данных, что-бы в результате решения иметь наилучшие планы для любого варианта исходных данных.

С математической точки зрения параметрическое программирование выступает как одно из средств анализа чувствительности решения к вариации исходных данных, оценки устойчивости решения.

Заметим, что существуют различные подходы к подобному анализу (например, на основе постановки двойственной задачи). Здесь мы, не ссылаясь на двойственные оценки, рассмотрим самые простейшие варианты решения для самых простейших параметрических программ.

Коэффициенты целевой функции линейно зависят от некоторого единственного параметра λ (времени, температуры и т. п.).

60. Что такое многокритериальная задача.

Задачи многокритериальной, или векторной, оптимизации возникают в тех случаях, когда имеется несколько целей, которые не могут быть отражены одним критерием (стоимость, надежность и т.п.)

Математически такая задача содержит область допустимых решений, которая может иметь любую природу, и несколько целевых функций, значение которых должно максимизироваться или минимизироваться в данной области. Максимизация и минимизация целевых функций легко сводятся друг к другу умножением на -1, поэтому, не нарушая общности, можно считать, что данная задача имеет вид:

Fi(x) →max (i= 1,2,…, n)

x ? D

x - ? ,

где D- область допустимых значений

61. Что такое рекорд в методе ветвей и границ.

Рекорд- это такое оптимальное значение целевой функции на частичной задачи, которое позволяет оставшиеся части более не рассматривать.

62. Приведите пример задачи целочисленного линейного программирования

Решить задачу ЦЛП:

f(x₁,x₂)= 2x₁+3x₂ → max,

5x₁+7x₂ ≤ 35,

4x₁+9x₂ ≤ 36,

x₁, x₂ ≥ 0,

x₁,x₂ - целые

Задачу решить можно методом прямого перебора. Организуем 2 цикла: 1-й по x1 от 0 до 9, 2-й, встроенный в первый, - по x2 от 0 до 5. Оператор тела цикла проверяет, удовлетворяет ли точка (x₁, x₂) обоим неравенствам, вычисляется значении функции f(x₁, x₂) и сравнивается с запомненным наилучшим решением.

63. Приведите пример задачи параметрического линейного программирования

Параметрическое программирование представляет собой один из разделов математического программирования, изучающий задачи, в которых целевая функция или ограничения зависят от одного или нескольких параметров.

Рассмотрим задачу минимизации

L(X, λ) = λX₁ - λX₂ - λX₃ + λX₄

при условиях

3X₁ - 3X₂ - X₃ + X₄ ≥ 5;

2X₁ - 2X₂ + X₃ - X₄ ≤ 3;

X_k ≥ 0, k = 1 ... 4; -∞ < λ < ∞.

64. Приведите пример многокритериальной задачи

z₁= 4x₁+10x₂ → max

z₂=x₁+x₂ →max

x₁+2x₂ ≤ 40

x₁, x₂ ? Z

x₁, x₂ ≥0

x₁, x₂ - ?

65. Сформулируйте условие окончания ветвления при решении задач методом ВИГ.

Основная идея метода «ветвей и границ» состоит в разбиении множества допустимых решений на подмножества, которые, в свою очередь, разбиваются на подмножества и т.д. При этом среди возникающих подмножеств могут быть такие, которые не содержат допустимых решений или заведомо не содержат оптимальных решений. Если это удается определить на некотором этапе с помощью тех или иных оценок, то такие подмножества исключаются из дальнейшего рассмотрения. В результате решение находится частичным перебором.

Критерии окончания ветвления:

В задаче на максимум в начале решения граничное значение целевой функции, или рекорд, полается равным - ∞ .

1. Получена задача, не имеющая решения. Это становится все более вероятным с увеличением глубины ветвления, когда все большее число ограничений вида x_i ≤ [{x_i⁰] , или x_i ≥ [{x_i⁰] +1 добавляется к уже существующим ограничениям( так, что все более вероятным становится несовместимость системы ограничений получаемых задач).

2. Если находится новое целочисленное решение, то оно сравнивается с рекордом; если прежний рекорд превзойден, то запоминается новый рекорд, в противном случае остается старый.

3. Получаемое оптимальное нецелочисленное решение задачи на какой-то стадии ветвления сравнивается с рекордом; если это значение меньше, чем рекорд, то ветвление задачи прекращается, так как нет возможности побить рекорд.

Непобитый рекорд дает оптимальное решение исходной задачи ЦЛП.

66. Что такое решение, оптимальное по Парето в многокритериальной задаче.

Множество допустимых решений, для которых невозможно одновременно улучшить все частные показатели эффективности, принято называть областью Парето или областью компромиссов, а принадлежащие ей решения – эффективными или оптимальными по Парето.

67. Объясните, почему метод ВИГ принадлежит к методам отсечения?

Вообще, отсечение- отбрасывание части допустимой области. Применяется это тогда, когда нужно найти целочисленное решение.

Метод ВИГ принадлежит к методам отсечения потому, что при решении задачи этим методом, допустимая область делится на части и при решении задачи для каждой отдельной части, мы оставшиеся части временно не учитываем( т.е. отсекаем).

68. Почему нельзя решать задачу целочисленного ЛП, решив ее сначала как обычную задачу ЛП без учета целочисленности, а затем округлив полученное решение?

1) Потому что не известно в какую сторону округлять( в большую или в меньшую)

2) Можно выйти за пределы допустимой области

3) Оптимальное целочисленное решение может быть не в соседней точке, а через одну, две, десять и т.д.

69. Что такое решение, оптимальное по Парето, в многокритериальной оптимизации?

Задачи многокритериальной, или векторной, оптимизации возникают в тех случаях, когда имеется несколько целей, которые не могут быть отражены одним критерием (стоимость, надежность и т.п.)

Множество допустимых решений, для которых невозможно одновременно улучшить все частные показатели эффективности, принято называть областью Парето или областью компромиссов, а принадлежащие ей решения – эффективными или оптимальными по Парето.

Общий вид задачи многокритериальной оптимизации:

f_i(x) → max (i=1,2,…,n),

x ? D

x- ?

70. Описать метод ветвей и границ

Основная идея метода «ветвей и границ» состоит в разбиении множества допустимых решений на подмножества, которые, в свою очередь, разбиваются на подмножества и т.д. При этом среди возникающих подмножеств могут быть такие, которые не содержат допустимых решений или заведомо не содержат оптимальных решений. Если это удается определить на некотором этапе с помощью тех или иных оценок, то такие подмножества исключаются из дальнейшего рассмотрения. В результате решение находится частичным перебором.

71. Метод динамического программирования, функция состояния, уравнение Беллмана

Динамическое программирование представляет собой математический аппарат, разработанный для решения некоторого класса задач математического программирования путем их разложения на относительно небольшие и, следовательно, менее сложные задачи. Специфика метода динамического программирования состоит в том, что для отыскания оптимального управления планируемая операция разделяется на ряд последовательных шагов или этапов. Соответственно и сам процесс планирования операции становится многошаговым и развивается последовательно, от этапа к этапу, причем каждый раз оптимизируется управление только на одном шаге.

В основе динамического программирования лежат 2 принципа:

Первый- принцип оптимальности Беллмана: каковы бы ни были начальное состояние системы и принятое решение, все последующие решения на остальных шагах должны составлять оптимальную стратегию относительно состояния, возникающего в результате первого решения.

Второй- принцип вложения: природа задачи, допускающая использование метода динамического программирования, не меняется при изменении числа шагов.

Структура процессов, исследуемых методом динамического программирования, должна удовлетворять следующим условиям:

· небольшое число переменных

· * управляемый процесс- Марковский, т.е. предыстория не имеет значения при определении будущих действий

· * критерий эффективности J является аддитивным.

Состояние на каждом шаге характ-ся некоторой переменной величиной, кот. называется параметром состояния. Наилучший эффект на данном этапе вместе с уже рассмотренными шагами хар-ся функцией состояния. Решение конкретной задачи методом динамич. программирования сводится к выбору параметра состояния, составлению ф-ии состояния и рекурентных соотношений, связывающих ф-ии состояния для двух соседних последовательных этапов, и их применению для выбора оптимального управления.

72. Составить математическую модель и записать функциональное уравнение Беллмана (рекуррентное соотношение), расшифровать все переменные и функции, входящие в него для следующей задачи.

F(x₁, x₂, x₃, x₄) =f₁(x₁) + f₂(x₂) + f₃(x₃) + f₄(x₄)

x₁+x₂+x₃+x₄= Z(700)

g_k= max( f_k(x_k) + g_k-₁ (Z-x_k)) F= g₄(Z)

x_k= 0, 100, 200, 300, 400

G3 F3	0 100 200 300 400

g₃(400) =105

77. В чем отличие «условий неопределенности» от «вероятностных условий». Что такое полная неопределенность и частичная неопределенность?

Принять, выработать решение в условиях определенности- это фактически найти экстремум известной функции при установленных ограничениях. Когда же некоторые существенные обстоятельства принятия решений известны не полностью не полностью или случайны, то говорят, что решение принимается в условиях неопределенности. Иными словами, неопределенность- это отрицание определенности. Не все случайное можно измерить вероятностью. Неопределенность- более широкое понятие. Неопределенность того, какой цифрой вверх ляжет игральный кубик, отличается от неопределенности того, каково будет состояние российской экономики через 15 лет. Иначе говоря, уникальные единичные случайные явления связаны с неопределенностью, а массовые случайные явления обязательно допускают некоторые закономерности вероятностного характере.

Предположим, что в рассматриваемой схеме известны вероятности p_j того, что реальная ситуация развивается по варианту j. Именно такое положение называется частичной неопределенностью.

78. Что такое платежная матрица и матрица рисков, экономический смысл платежной матрицы

Предположим, что ЛПР рассматривает несколько (i=1,…,m) возможных решений. Ситуация неопределенная, понятно лишь, что наличествует какой-то из вариантов j=1,…,n. Если будет принято i-е решение в j-й ситуации, то фирма, возглавляемая ЛПР, получит доход q_ij. Матрица Q=|| q_ij || называется матрицей последствий( возможных решений). Какое же решение нужно принять ЛПР? В ситуации полной неопределенности могут быть высказаны лишь некоторые рекомендации предварительного характера. Они не обязательно будут приняты ЛПР. Многое будет зависеть, например, от его склонности к риску. Но как оценить риск в данной схеме?

Допустим, мы хотим оценить риск, который несет в себе i-е решение. Нам неизвестна реальная ситуация. Но если бы мы ее знали, то выбрали бы наилучшее решение, т.е. приносящее наибольший доход, в j-й ситуации было бы принято решение, дающее доход q_j= max{q_ij}. Значит, принимая i-е решение, мы рискуем получить не q_j, а только q_ij и недобрать r_ij=q_j-q_i. Матрица R=|| r_ij || называется матрицей рисков.

79. Как по платежной матрице составить матрицу рисков?

Пусть матрица последствий есть

5 2 8 4

Q= 2 3 4 12

8 5 3 10

1 4 2 8

Составим матрицу рисков. Имеем

q₁= max{q_i1}=8, q₂=5, q₃=8, q₄=12

Следовательно, матрица рисков

3 3 0 8

R= 6 2 4 0

0 0 5 2

7 1 6 4

80. Как рекомендуется принять решение по «Вальду»

Правило крайнего пессимизма. Рассматривая i-е решение, будем полагать, что на самом деле ситуация складывается самая плохая, т.е. приносящая самый малый доход

a_i = min_j{q_ij}.Но теперь среди ai выберем i₀-е решение с наибольшим a_ij. Итак, правило Вальда рекомендует принять i₀-е решение, такое, что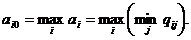

81. Как рекомендуется принимать решение «по Сэвиджу»?

Правило минимального риска. При применении этого правила анализируется матрица рисков R=|| r_ij ||. Рассматривавая i-е решение, будем полагать, что на самом деле складывается ситуация максимального риска b_i= max{r_ij}. Но теперь выберем i₀-е решение с наименьшим b_i0. Итак, Правило Севиджа рекомендует принять i₀-е решение, такое, что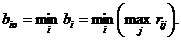

82. Как рекомендуется принимать решение «по Гурвицу»?

Взвешивающее пессимистический и оптимистический подходы к ситуации. Принимая i-е решение, при котором достигается max 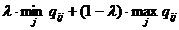, где 0 ≤ ג ≥1. Значение ג

выбирается из субъективных соображений. Если ג →1, то правило Гурвица приблежается к правилу Вальда, при ג →0 правило Гурвица приблежается к правилу «розового оптимизма».

83. Что такое правило «розового оптимизма»?

( 0 6 5 2 )

( 6 2 8 22)

( 9 4 3 32)

( -6 -4 -12 10)

ЛПР считает, что для него сложится самая благоприятная ситуация, т.е. он получит самый большой доход в результате своей деятельности c_i = max q_ij. Теперь выберем решение i₀ с наибольшим c_i0. Итак, правило “розового оптимизма рекомендует принять решение i₀ такое, что c_i0 = max (max q_ij). Так, в вышеуказанном примере имеем с₁ = 6, с₂ = 22, с₃ = 32, с₄ = 10. Теперь из чисел 6, 22, 32, 10 берем максимальное. Это — 32. Значит, правило “розового оптимизма” рекомендует 3-е решение.

84.Как находится риск финансовой операции как среднее квадратическое?

Существует ещё одно понимание риска. Рассмотрим какую-либо операцию, доход которой есть случайная величина Q. Как мы знаем средний ожидаемый доход- математическое ожидание случайной величины MQ а вот среднее квадратическое отклонение (СКО) σQ=√DQ- это мера разброса возможных значений дохода вокруг среднего ожидаемого дохода mQ.

Напомним что DQ=M(Q-MQ)².среднее квадратичное отклонение дохода от операции r1=√DQi в данном случае и будет служить определение меры риска.

85. Что такое доминирование финансовых операций?

При расчете средних доходов и рисков, получаем средние ожидаемые доходы и риски и строим на графике( Q= q откладываем по горизонтали, а риск r- по вертикали.) Получили четыре точки. Чем правее расположена точка ( q, r), тем более доходной операции она соответствует, чем выше расположена точка- тем с большим риском связана эта операция. Значит нужно выбирать точку правее и ниже.

Точка (q’, r’) доминирует точку (q, r) если q’ ≥ q и r’≤ r и хотя бы одно из этих неравенств строгое.

Точка, не доминируемая никакой другой, называется оптимальной по Парето, а множество всех таких точек( операций) наз. множеством, оптимальным по Парето.

86. Что такое взвешивающая формула?

Если из рассмотренных операций необходимо выбрать лучшую, то ее надо обязательно выбирать из операций, оптимальных по Парето. Для нахождения лучшей операции иногда применяют подходящую взвешивающую формулу. Для пар (q, r) данная формула дает одно число, по которому и определяют лучшую операцию.

Пример использования взвешивающей формулы( пример задачи 10.3 стр 425 :-) ) :

Пусть взвешивающая формула есть Φ(q, r)= q-r

Вычисляем, получаем

Φ(Q₁)= 4.83-1.77= 3.064 ; Φ(Q₂)= 0.6; Φ(Q₃)= 4.7; Φ(Q₄)= 0.27

и лучшей операцией оказывается третья.

87. Каков экономический смысл среднего ожидаемого дохода финансовой операции? Формула для его расчета

При многократном повторении всей ситуации, котор. применяется в этой операции, доход будет примерное равен рассчитанному среднему.

Q1=∑Q_{i *} p_i , p- вероятность, q- доходность

88. Как рекомендуется принимать решение по критерию наибольшего среднего ожидаемого дохода?

Правило максимизации среднего ожидаемого дохода.

Доход, получаемый фирмой при реализации i-го решения, является случайной величиной Qi с рядом распределения

q_i1 … q_in

p₁ … p_n

Математическое ожидание MQ_i есть средний ожидаемый доход. Рассматриваемое правило рекомендует принять решение, приносящее максимальный средний ожидаемый доход.

89. Верхняя и нижняя цена игры в матричной игре в чистых стратегиях, их нахождение.

Стратегия называется чистой, если выбор игрока неизменен от партии к партии. У первого игрока, очевидно, есть m чистых стратегий, у второго – n.

При анализе игр противник считается сильным, т.е. разумным.

Рассмотрим описанную конфликтную ситуацию с точки зрения первого игрока. Если мы( первый игрок) выбираем свою i-ю стратегию (i-ю строку матрицы А), то второй игрок, будучи разумным, выберет такую стратегию j, которая обеспечит ему наибольший выигрыш ( а нам наименьший), т.е. он выберет такой столбец j матрицы А, в котором платеж a_ij( второго игрока первому) минимален. Переберем все наши стратегии i= 1,2,,..,m и выберм ту из них, при которой второй игрок, действуя максимально разумно, заплатит нам наибольшую сумму. Величина α = max_i=1,2,…n min_j=1,2,…m a_ij называется нижней ценой игры, а соответствующая ей стратегия первого игрока- максиминной. Аналогичный рассуждения( но уже с точки зрения второго игрока) определяют верхнюю цену игры

β = min_j=1,2,…n max_i=1,2,…m a_ij и соответствующую ей минимаксную стратегию второго игрока.

По своему определению нижняя цена игры α представляет собой максимальный гарантированный выигрыш первого игрока( т.е. применяя свою максиминную стратегию, первый игрок обеспечивает себе выигрыш, не меньший α), а верхняя цена- величину, противоположную минимальному гарантированному проигрышу второго игрок( т.е. применяя свою минимаксную стратегию, второй игрок гарантивует, что он не проиграет больше, чем β ,или, иначе, выиграет не меньше , чем (-β)).

90. Оптимальные стратегии в матричной игре в чистых стратегиях, условие их существования, седловая точка матрицы.

Если α= β, то говорят, что игра имеет седловую точку в чистых стратегиях. Общее значение α и β называется ценой игры и обозначается v= α= β . При этом стратегии игроков, соответствующие седлововой точке, называются оптимальными чистыми стратегиями, так как эти стратегии являются наиболее выгодными сразу для обоих игроков, обеспечивая первому игроку гарантированный выигрыш не менее v, а второму игроку- гарантированный проигрыш не более (-v), и отклоняться игрокам от этих стратегий невыгодно.

91. Дана матрица, один из элементов которой является параметром. Найти область значений параметра (с доказательством), при которых заданные стратегии игроков будут оптимальными.