Вторая основная теорема двойственности (о дополняющей нежесткости) и ее экономическое истолкование.

Для того чтобы допустимые решения исходной 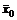и двойственной 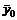задач являлись оптимальными решениями соответствующих задач двойственной пары необходимо и достаточно выполнение следующих условий:

;

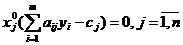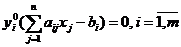
Т.е. если какое-либо нер-во системы ограничений одной из задач не обращается в точное равенство оптимальным решением этой задачи, то соответствующая компонента оптимального решения двойственной задачи должна быть равна 0. Если же какая-либо компонента оптимального решения положительна, то соотв-ее ей ограничение в двойственной задаче должно быть обращено в точное равенство.

Другими словами: 1)если х_j⁰>0,то 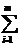a_ijy_i⁰=c_j; 2)если 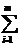a_ijy_i⁰>c_j , то x_j⁰=0; 3)если y_i⁰>0, то 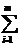a_ijx_j⁰=b_i; 4)если 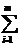a_ijx_j⁰<b_i,то y_i⁰=0. j= 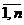, i=

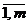
Если по оптимальному плану расход i-того ресурса < его запасов, то оценка этого ресурса=0. Если же оценка>0, то расход этого ресурса равен его запасу. Таким образом, дефицитный (полностью используемый по оптимальному плану) ресурс имеет положительную оценку в двойственной задаче, а недефицитный – нулевую оценку.

С точки зрения пр-ва: если оценка ресурсов, расходуемых по j-ой технологии больше цены продукта, то j-ая технология не применяется (x_j=0). Если же по некот. плану j-ая технология применяется (x_j>0), то оценка ресурсов, расходуемых по данной технологии, равна цене продукта.

Эта т-ма вместе с еще 2-мя теоремами и образует так называемую т-ию двойственности ЛП.

45.Третья основная теорема двойственности (об оценках влияния ресурсов на выпуск продукции) и ее экономическое содержание (без доказательства). Перераспределение ресурсов между предприятиями фирмы с помощью двойственных оценок ресурсов.

Значения переменных y_i⁰ в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов (правых частей b_i) системы ограничений исходной задачи на величину максимума целевой функции: 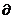z_max/ 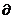b_i =y_i⁰ , при этом увеличение правой части i-го ограничения приводит к увелич. или уменьш. z_max в зависимости от того будет ли y_i⁰ положит. или отрицательным.

Экон.смысл: двойственная оценка ресурса – это приращение прибыли, приходящейся на единицу приращения этого ресурса. Здесь речь идет лишь о достаточно малых приращениях ресурсов, так как изменение величины 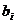в некоторый момент вызовет изменение оценок 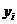. Оценки позволяют выявить направление мероприятий по расшивке узких мест производства (ресурсы с положительной двойственной оценкой), обеспечивающих получение наибольшего экономического эффекта.

Эта т-ма вместе с еще 2-мя теоремами и образует так называемую т-ию двойственности ЛП.

Из 2-ой и 3-ей теорем следует, что часть ресурсов, у которых двойственные оценки будут отличны от 0, необходимо будет пополнять для продолжения выпуска продукции. Недостающие ресурсы должны быть пополнены, причем в оптимальном количестве.