В каких задачах находится симплекс-метод?

В задачах линейного программирования.Для задач,связанных с принятием решений в экономике,характерна ситуация,когда требуется достичь некоторой цели при ограниченных ресурсах.Если функция цели линейно зависит от переменных (размеров видов деятельности или производственных процессов) и расходы ресурсов также линейно зависят от переменных,то такая задача принятия решений сводится к задаче линейного программирования(ЛП).

36.Что представляет собой симплексная таблица

Симплекс-таблица составляется из коэффициентов при x₁, x₂, x₃, x₄ и чисел, стоящих в правых частях уравнений-ограничений задачи: в первой строке записываются элементы уравнения (А), во второй - (В). В последней строке симплекс-таблицы записываются коэффициенты и правая часть целевой функции (С). Таким образом, симплекс-таблица содержит две строки коэффициентов (по числу ограничений задачи) и строку коэффициентов целевой функции. Число столбцов в симплекс-таблице равно числу переменных задачи плюс один столбец правых частей (b):

Запишите симметричную пару двойственных задач линейного программирования.

Прямая задача имеет ограничение ≤, целевая функция максимальна

Двойственная ≥,цифровая функция минимальна

2х1+3х2+8х3≥50 y1

4х1-7х2+9х3≤ у2

F=100х1+200х2+300х3=>max

Х1,2,3≥0

2у1+4у2≥100

3у1-7у2≥200

8у1+9у2≥300

G=50у1+60у2=>min

Двойственные (расчетные) оценки ресурсов. Симметричная пара двойственных задач ЛП. Несимметричная пара двойственных задач ЛП, правила составления двойственной задачи для данной задачи ЛП со смешанными ограничениями.

Теория двойственности является центральной частью всего ЛП. Она имеет богатое экономическое содержание.

В рамках модели ЛП предприятия должна существовать внутренняя система оценки ресурсов, используемых им в процессе производства. Эти оценки связаны с технологическими особенностями данного производственного процесса, характеризуемыми матрицей условий A, со структурой и количеством ресурсов, отпущенных для производственного потребления, описываемых вектором B, а также со структурой внешних цен, на основе которых получается вектор прибылей C. Эти оценки называют расчетными оценками ресурсов. Расчетную оценку единицы ресурса не следует отождествлять с той ценой, по которой предприятию был отпущен этот ресурс. Последняя отражает общественно необходимые затраты на производство единицы ресурса, а расчетная цена показывает только сравнительную ценность этого ресурса на данном предприятии в данных конкретных условиях.

В зависимости от вида исходной задачи линейного программирования различают симметричные и несимметричные пары двойственных задач.

Если система ограничений исходной задачи состоит из неравенств и на все переменные х_j наложено условие неотрицательности, то исходная задача и составленная по определенному правилу двойственная задача образуют симметричную пару двойственных задач.

Пусть исходная задача имеет вид: найти наибольшее значение функции

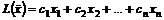
при ограничениях:

.

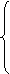
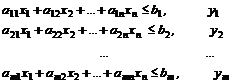
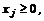
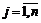Правило составления двойственных задач

1. Каждому ограничению исходной задачи ставится в соответствие двойственная переменная y_i, где .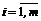

2. Составляется целевая функция 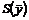, коэффициентами которой будут свободные члены системы ограничений исходной задачи, а цель задачи меняется на противоположную:

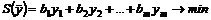. (1)

3. Составляется система ограничений двойственной задачи, при этом матрица из коэффициентов системы ограничений исходной задачи транспонируется, знак неравенства меняется на противоположный, свободными членами будут являться коэффициенты из целевой функции исходной задачи:

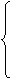
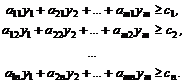₍₂₎

4. Переменные y_i в двойственной задаче также неотрицательны, т.е.

. (3)

Если двойственную задачу принять за исходную и по данному правилу составить двойственную задачу, то получим исходную задачу. Понятие двойственности является взаимным.

В несимметричном случае двойственная задача составляется по тем же правилам, что и в случае симметричной пары, но если двойственная переменная поставлена в соответствие ограничению уравнения, то эта переменная свободна по знаку.

39.Матричная запись пары двойственных задач ЛП (симметричная пара задач с ограничениями-неравенствами и нессиметричная пара,где в одной из задач ограничения имеют вид равенств)

Прямая Двойствен

AX≤И A*Y≥C

х≥0 Y≥0

F=CX=>max G=B*Y=>min

Если среди неравенств есть 1 равенство,то нессиметричная пара.

2х1+3х2+8х3≤50 у1

4х1-7х2+9х3=60 у2

40,41,42.Основное неравенство теории двойственности ЛП. Малая теорема двойственности и ее экономическое содержание. Теорема о достаточном условии оптимальности решений пары двойственных задач ЛП.

Для любых допустимых решени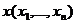й и 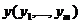прямой и двойственной задач ЛП справедливо неравенство: 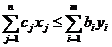. Для любого допустимого плана исходной задачи и для любого допустимого в-ра оценок ресурсов 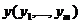общая стоимость всего произведенного продукта не превышает суммарной стоимости ресурсов.

Малая теорема двойственности: Для существования оптимального решения пары двойственных задач необходимо и достаточно существование допустимого решения для каждой из них.

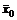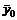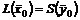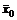Теорема о достаточном условии оптимальности решений пары двойственных задач: Если и - допустимые решения пары двойственных задач, для которых выполняется равенство , то и 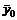- оптимальные решения соответствующих задач.

Согласно этой теореме, план производства продукции и вектор оценок ресурсов является оптимальным, если цена всей произведенной продукции и суммарная оценка ресурсов совпадают.