Экстремальные пути в нагруженных ориентированных графах
ТЕМА 7. ТЕОРИЯ ГРАФОВ
Основные понятия теория графов
Теория графов – это математический аппарат для формализации (моделирования) реальных задач по исследованию свойств конечных множеств с заданными отношениями между их элементами. В их числе задачи из области администрирования сетей, информационных потоков, планирования, проектирования и управления различными системами.
Первая работа по теории графов принадлежащая Эйлеру, появилась в 1736 году. Вначале эта теория была связана с математическими головоломками и играми. Однако впоследствии теория графов стала использоваться в топологии, алгебре, теории чисел. В наше время теория графов находит применение в самых разнообразных областях науки, техники и практической деятельности. Она используется при проектировании электрических сетей, планировании транспортных перевозок, построении молекулярных схем. Применяется теория графов также в информатике, экономике, психологии, социологии, биологии.
Задачи на графах удобно переводить на языки программирования, то есть решать с использованием современной вычислительной техники. Умение решать задачи на графах, в том числе и на персональных ЭВМ позволит будущему специалисту приобрести опыт разработки технологий и методов теории операций для решения задач при научных исследованиях и проектно-конструкторской деятельности.
Графы помогают описывать и исследовать различные системы объектов и их связи. Например, в графе, изображенном на рис. 13, точки (вершины графа) можно интерпретировать как города, а линии, соединяющие вершины (ребра), как дороги, соединяющие эти города.
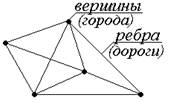
Рис. 13
Формальное определение графа таково: Графом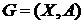 
называется пара множеств: 
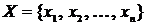– множество, элементы которого называются вершинами, 
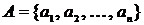– множество неупорядоченных пар вершин, называемых ребрами.
Для многих задач несущественно, являются ли ребра отрезками прямых или криволинейными дугами; важно лишь то, какие вершины соединяет каждое ребро.
Если ребрам графа приданы направления от одной вершины к другой, то такой граф называется ориентированным,т.е.подмножество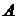 
представляет собой упорядоченные пары. Ребра ориентированного графа называются дугами. Соответствующие вершины ориентированного графа называют началоми концом. Если направления ребер не указываются, то граф называется неориентированным (или просто графом). Неориентированное ребро графа эквивалентно двум противоположно направленным дугам, соединяющим те же самые вершины. Множество ребер графа может быть пустым. Множество вершин графа не может быть пустым.
Граф, имеющий как ориентированные, так и неориентированные ребра, называется смешанным.
Пример. На рис. 14 изображен неориентированный граф .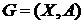 
, 
.
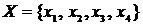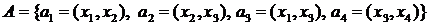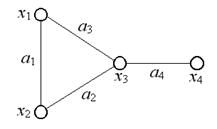
Рис. 14. Неориентированный граф
Пример. На рис. 15. изображен ориентированный граф . ,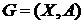 
.
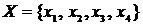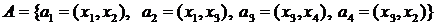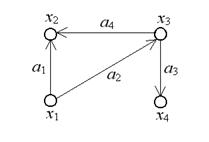
Рис. 15. Ориентированный граф
Пример. На рис. 16. изображен ориентированный граф . ,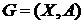 
.
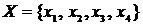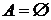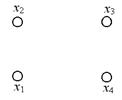
Рис. 16. Граф с пустым множеством дуг
Как в случае ориентированного, так и в случае неориентированного ребра говорят, что вершины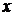 
и 
и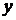нцидентныребру 
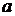, если эти вершины соединены 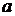. Две вершины называются смежными, если они инцидентны одному и тому же ребру. Два ребра называются смежными, если они имеют общую вершину. Степенью вершины графа 
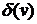называется число ребер, инцидентных этой вершине. Вершина, имеющая степень 0, называется изолированной, а степень 1 – висячей. Полустепенью исхода (захода) вершины 
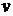ориентированного графа 
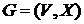называется число 
( 
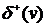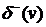) дуг ориентированного графа 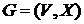, исходящих из 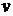(заходящих в ).
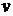Для ориентированного графа множество вершин, в которые ведут дуги, исходящие из вершины 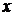, обозначают 
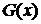, то есть 
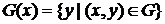. Множество 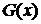называют образом вершины 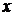. Соответственно 
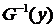– множество вершин, из которых исходят дуги, ведущие в вершину 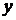, то есть 
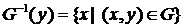. Множество 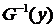называют прообразомвершины .
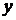Пример. В графе, изображенном на рис. 14, концами ребра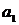 
являются вершины 
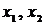; вершина 
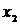инцидентна ребрам 
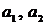; степень вершины 
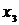равна3;вершины 
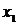и 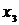смежные; ребра 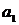и 
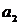смежные; вершина 
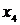висячая. В ориентированном графе, изображенном на рис. 15, началом дуги 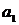является вершина 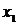, а ее концом - вершина x2; вершина x1инцидентна дугам 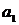и ; 
, 
, 
, 
.
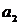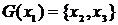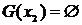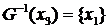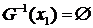Если множеству 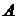принадлежат пары 
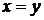, то такие ребра 
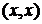называют петлями. Существование одинаковых пар 
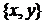соответствует наличию параллельных или кратных ребер (дуг), а кратностью ребер называют количество таких одинаковых пар.
Например, кратность ребра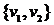 
в графе, изображенном на рис. 17, равна двум, кратность ребра 
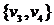равна трем.
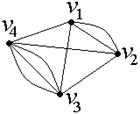
Рис. 17. Граф с кратными ребрами
Граф, содержащий кратные ребра, называется мультиграфом. Граф с кратными ребрами и петлями называетсяпсевдографом. Следует заметить, что в случае ориентированного псевдографа вклад каждой петли инцидентной вершине 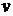равен 1 как в 
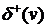, так и в 
.
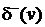Подграфомнеориентированного графа 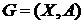называется граф, все вершины и ребра которого содержатся среди вершин и ребер графа 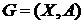. Аналогично определяется подграф ориентированного графа. Подграф называется собственным, если он отличен от самого графа. Граф 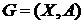– полный, если для любой пары вершин 
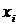и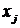 
существует ребро 
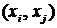. Граф 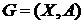– симметрический, если для любой дуги 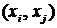существует противоположно ориентированная дуга 
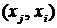. Граф 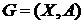– планарный, если он может быть изображен на плоскости так, что не будет пересекающихся дуг. Неориентированный граф 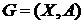– двудольный, если множество его вершин 
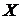можно разбить на два такие подмножества 
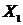и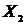 
, что каждое ребро имеет один конец в 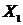, а другой в .
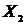7.2. Матричные способы задания графов
Для алгебраического задания графов используются матрицы смежности и инцидентности.
Матрица смежности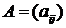 
определяется одинаково для ориентированного и неориентированного графов. Это квадратная матрица порядка 
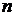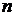, где – число вершин, у которой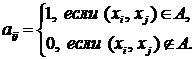 
Пример. Матрица смежности графа, изображенного на рис. 14, имеет вид: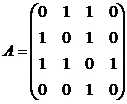 
.
Пример. Матрица смежности ориентированного графа, изображенного на рис. 15, имеет вид: 
.
Отметим, что матрица смежности полностью задает граф.
Матрицей инцидентности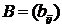 
ориентированного графа называется прямоугольная матрица 
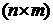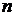, где – число вершин, 
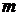– число ребер, у которой
Для неориентированного графа матрица инцидентности 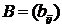задается следующим образом:
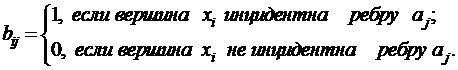
Пример. Матрица инцидентности графа, изображенного на рис. 14, имеет вид: 
.
Пример. Матрица инцидентности ориентированного графа, изображенного на рис. 15, имеет вид: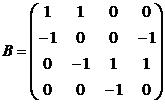 
.
Матрица инцидентности, так же, как и матрица смежности, полностью задает граф. Матрицы смежности и инцидентности удобны для задания графов на ЭВМ.
Основные свойства матриц смежности и инцидентности:
1. Матрица смежности неориентированного графа является симметричной. Для ориентированного графа это, вообще говоря, неверно.
2. Сумма элементов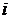 
-ой строки или 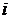-го столбца матрицы смежности неориентированного графа равна степени вершины 
.
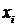3. Сумма элементов 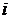-ой строки матрицы смежности ориентированного графа равна числу дуг, исходящих из .
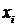4. Сумма элементов 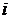-го столбца матрицы смежности ориентированного графа равна числу дуг, входящих в вершину xi.
5. Сумма строк матрицы инцидентности ориентированного графа является нулевой строкой.
Итак, возможны следующие различные способы задания графа:
а) посредством графического изображения;
б) указанием множества вершин и множества ребер (дуг);
в) матрицей смежности;
г) матрицей инцидентности.
Изоморфизм графов
Графы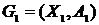 
и 
и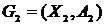зоморфны, если существует взаимно однозначное соответствие между множествами вершин 
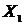и 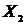, такое, что любые две вершины одного графа соединены тогда и только тогда, когда соответствующие вершины соединены в другом графе.
Пример. Графы, изображенные на рис. 18 являются изоморфными.
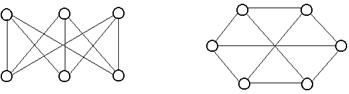
Рис. 18. Изоморфные графы
Изоморфные графы отличаются только нумерацией вершин. Матрицы смежности двух изоморфных графов могут быть получены одна из другой перестановкой строк и столбцов. Чтобы узнать, являются ли два графа изоморфными, нужно произвести все возможные перестановки строк и столбцов матрицы смежности одного из графов. Если после какой-нибудь перестановки получится матрица смежности второго графа, то эти графы изоморфны. Чтобы убедиться, что графы неизоморфны, надо выполнить все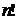 
возможных перестановок строк и столбцов.
Маршруты и пути
Пусть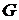 
– неориентированный граф. Маршрутомили цепьюв 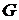называется такая последовательность (конечная или бесконечная) ребер 
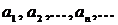, что каждые соседние два ребра 
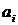и 
и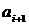меют общую инцидентную вершину. Одно и то же ребро может встречаться в маршруте несколько раз. В конечном маршруте ( 
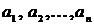) имеется первое ребро 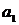и последнее ребро 
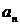. Вершина 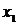, инцидентная ребру 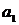, но не инцидентная ребру 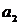, называется началом маршрута, а вершина 
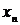, инцидентная ребру 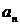, но не инцидентная ребру 
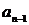, называется концом маршрута.
Длиной(или мощностью) маршрута называется число ребер, входящих в маршрут, причем каждое ребро считается столько раз, сколько оно входит в данный маршрут.
Пример. В изображенном на рис. 19 графе рассмотрим два маршрута из вершины 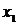в вершину 
: 
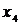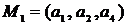и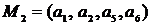 
. Длина маршрута 
равна 3, а длина маршрута 
равна 4.
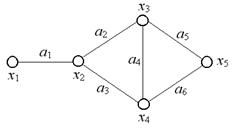
Рис. 19
Замкнутый маршрут называется циклом.
Маршрут (цикл), в котором все ребра различны, называется простой цепью (циклом). Маршрут (цикл), в котором все вершины, (кроме первой и последней), различны, называется элементарной цепью (циклом).
Пример. В приведенном на рис 20 графе выделим следующие маршруты: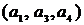 
– простая элементарная цепь длины 3, т.к. все ребра и вершины попарно различны; 
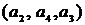– простой элементарный цикл, т.к. это замкнутый маршрут, у которого все ребра и вершины, кроме первой и последней, различны; 
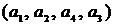– цепь, которая является простой, но не элементарной, т.к. все ребра различны, но вершина 
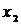встречается дважды; 
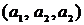– маршрут длины 3, не являющийся ни простой, ни элементарной цепью, т.к. ребро 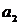и вершина 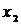встречаются дважды.
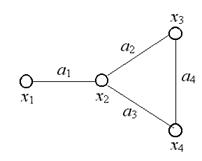
Рис. 20. Маршруты в неориентированном графе
Понятия пути, контура в ориентированном графе аналогичны понятиям маршрута, цикла в неориентированном графе.
Путемориентированного графа называется последовательность дуг, в которой конечная вершина всякой дуги, отличной от последней, является начальной вершиной следующей дуги. Число дуг пути называетсядлиной пути.
Путь называется контуром, если его начальная вершина совпадает с конечной вершиной. Путь (контур), в котором все дуги различны, называетсяпростым. Путь (контур), в котором все вершины, кроме первой и последней, различны, называетсяэлементарным.
Следует усвоить, что понятиям ребра, маршрута, цепи, цикла в неориентированном графе соответствуют понятия дуги, пути, ориентированной цепи, контура в ориентированном графе. Для лучшего запоминания приведем эти термины в таблице.
| Неориентированный граф | Ориентированный граф |
| ребро маршрут цикл | дуга путь контур |
Пример. В приведенном на рис. 21 графе выделим следующие пути: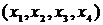 
– простой элементарный путь, т.к. каждая вершина и каждая дуга используются не более одного раза; 
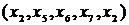– простой элементарный контур, т.к. это замкнутый путь, в котором все дуги и вершины, кроме первой и последней, различны.
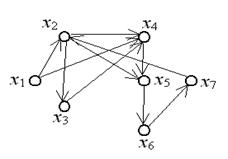
Рис. 21. Пути в ориентированном графе
Связность графа
Неориентированный граф называется связным, если каждая пара различных вершин может быть соединена, по крайней мере, одной цепью.
Ориентированный граф называется сильно связным, если для любых двух его вершин 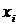и 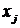существует хотя бы один путь, соединяющий 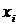с 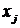. Ориентированный граф называется односторонне связным, если для любых двух его вершин, по крайней мере, одна достижима из другой.
Компонентой связности неориентированного графа называется его связный подграф, не являющийся собственным подграфом никакого другого связного подграфа данного графа (максимально связный подграф).
Компонентой сильной связности ориентированного графа называется его сильно связный подграф, не являющийся собственным подграфом никакого другого сильно связного подграфа данного графа (максимально сильно связный подграф).
Компонентой односторонней связности ориентированного графаназывается его односторонне связный подграф, не являющийся собственным подграфом никакого другого односторонне связного подграфа данного графа (максимально односторонне связный подграф).
Пусть 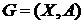неориентированный граф с множеством вершин 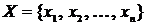. Квадратная матрица 
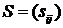порядка 
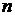, у которой
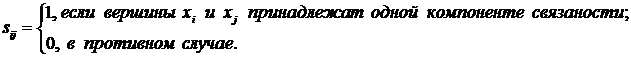называется матрицей связностиграфа .
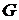Для ориентированного графа квадратная матрица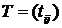 
порядка 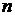, у которой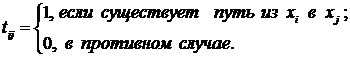 
называетсяматрицей односторонней связности (достижимости).
Квадратная матрица 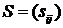порядка 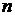, у которой
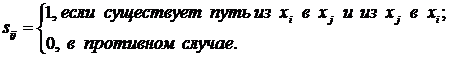
называется матрицей сильной связности.
Пример. У неориентированного графа, изображенного на рис. 22 две компоненты связности. Первая компонента связности включает вершины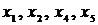 
,а вторая состоит из одной вершины .
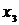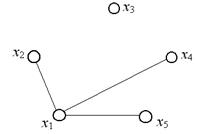
Рис. 22. Компоненты связанности неориентированного графа
Матрица связности этого графа имеет вид: 
.
Мы видим, что 1-ая, 2-ая, 4-ая и 5-ая строки матрицы одинаковы.
Пример. У ориентированного графа, изображенного на рис. 23 две компоненты сильной связности. Первая компонента связности включает вершины 
,а вторая состоит из одной вершины 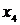. Действительно, для любой пары вершин из множества 
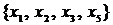существует хотя бы один путь, соединяющий эти вершины. Например, путь 
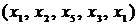соединяет все эти вершины. Из вершины 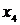нет пути ни в одну вершину графа.
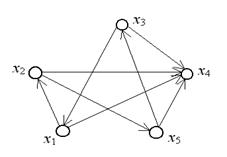
Рис. 23. Компоненты сильной связанности ориентированного графа
Матрица сильной связности этого графа имеет вид:
.
Заметим, что 1-ая, 2-ая, 3-ая и 5-ая строки матрицы 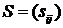одинаковы.
Для того, чтобы выделить компоненты сильной связности, необходимо сначала найти матрицу достижимости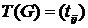 
ориентированного графа, затем находим матрицу сильной связности 
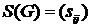ориентированного графа (она должна быть симметрической).
Алгоритм выделения компонента сильной связности:
1. Присваиваем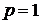 
( 
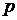− количество компонент связности), 
.
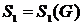2. Включаем в множество вершин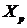 
компоненты сильной связности 
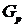вершины, соответствующие единицам первой строки матрицы 
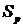. В качестве матрицы смежности 
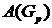возьмем подматрицу матрицы 
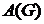, состоящую из элементов матрицы 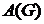, находящихся на пересечении строк и столбцов, соответствующих вершинам из .
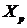3. Вычеркиваем из 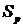строки и столбцы, соответствующие вершинам из 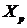. Если не остается ни одной строки (и столбца), то 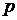- количество компонент сильной связности. В противном случае обозначим оставшуюся после вычеркивания срок и столбцов матрицу как 
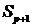, присваиваем 
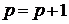и переходим к п. 2.
Пример. Выделим компоненты связности ориентированного графа, изображенного на рис. 25. Количество вершин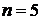 
.
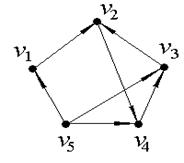
Рис. 25.
Значит, для данного ориентированного графа матрица смежности будет иметь размерность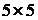 
и будет выглядеть следующим образом
.
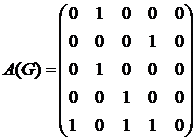Найдем матрицу достижимости и матрицу сильной связности для данного ориентированного графа:
, 
.
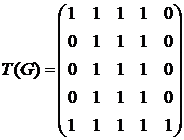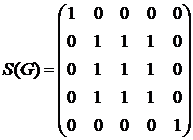Присваиваем ,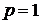 
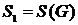и составляем множество вершин первой компоненты сильной связности 
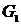: это те вершины, которым соответствуют единицы в первой строке матрицы 
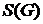. Таким образом, первая компонента сильной связности состоит из одной вершины 
.
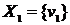Вычеркиваем из матрицы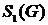 
строку и столбец, соответствующие вершине 
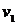, чтобы получить матрицу 
.
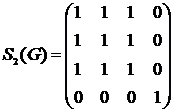Присваиваем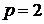 
. Множество вершин второй компоненты связности составят те вершины, которым соответствуют единицы в первой строке матрицы 
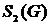, то есть 
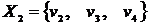. Составляем матрицу смежности для компоненты сильной связности 
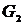исходного графа 
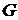− в ее качестве возьмем подматрицу матрицы 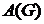, состоящую из элементов матрицы 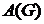, находящихся на пересечении строк и столбцов, соответствующих вершинам из :
.
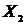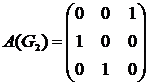Вычеркиваем из матрицы 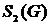строки и столбцы, соответствующие вершинам из ,чтобы получить матрицу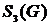 
, которая состоит из одного элемента 
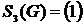, присваиваем 
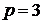. Таким образом, третья компонента сильной связности исходного графа, как и первая, состоит из одной вершины 
.
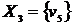Таким образом, выделены 3 компоненты сильной связности ориентированного графа :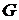
 :  |  :  |  :  |
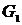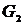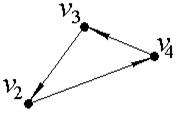Алгоритм Краскала.
Шаг 1. Установка начальных значений. Вводится матрица длин ребер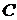 
графа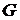 
.
Шаг 2. Выбрать в графе 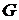ребро минимальной длины. Построить граф 
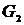, состоящий из данного ребра и инцидентных ему вершин. Положить 
.
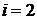Шаг 3.Если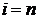 
, где 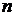– число ребер графа, то закончить работу (задача решена), в противном случае перейти к шагу 4.
Шаг 4. Построить граф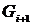 
, добавляя к графу 
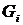новое ребро минимальной длины, выбранное среди всех ребер графа 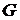, каждое из которых инцидентно какой-нибудь вершине графа 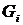и одновременно инцидентно какой-нибудь вершине графа 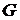, не содержащейся в 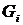. Вместе с этим ребром включаем в 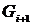и инцидентную ему вершину, не содержащуюся в 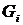. Присваиваем 
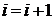и переходим к шагу 3.
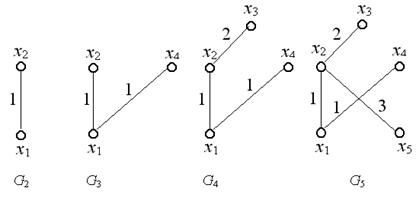
Пример. Найдем минимальное остовное дерево для графа, изображенного на рис. 36.
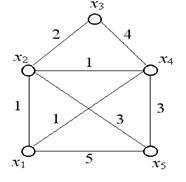
Рис. 36
Шаг 1. Установка начальных значений. Введем матрицу длин ребер :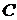
С =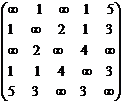 
.
Шаг 2. Выберем ребро минимальной длины. Минимальная длина ребра равна единице. Таких ребер три: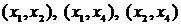 
. В этом случае можно взять любое. Возьмем 
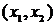. Построим граф 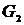, состоящий из данного ребра и инцидентных ему вершин 
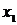и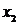 
. Положим 
.
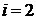Шаг 3. Так как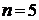 
, то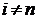 
, поэтому переходим к шагу 4.
Шаг 4. Строим граф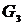 
, добавляя к графу 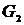новое ребро минимальной длины, выбранное среди всех ребер графа 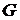, каждое из которых инцидентно одной из вершин 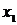, 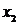и одновременно инцидентно какой-нибудь вершине графа 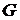, не содержащейся в 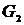т. е. одной из вершин 
, 
, 
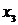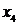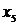. Таким образом, нужно выбрать ребро минимальной длины из ребер 
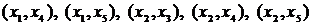. Таких ребер длины единица два: 
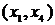и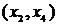 
. Можно выбрать любое. Возьмем 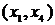. Вместе с этим ребром включаем в вершину 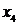, не содержащуюся в 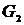. Полагаем 
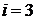и переходим к шагу 3.
Шаг 3. Так как 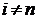, поэтому переходим к шагу 4.
Шаг 4. Строим граф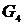 
, добавляя к графу 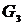новое ребро минимальной длины из ребер 
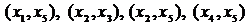. Такое ребро длины два одно: 
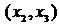. Вместе с этим ребром включаем в 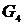вершину 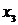, не содержащуюся в 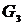. Полагаем 
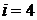и переходим к шагу 3.
Шаг 3. Так как 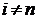, поэтому переходим к шагу 4.
Шаг 4. Строим граф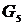 
, добавляя к графу 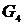новое ребро минимальной длины из ребер 
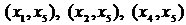. Таких ребер длины три два: 
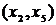и 
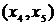. Возьмем 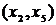. Вместе с этим ребром включаем в 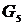вершину 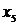, не содержащуюся в 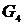. Полагаем 
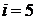и переходим к шагу 3.
Шаг 3. Так как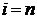 
, то граф 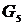– искомое минимальное остовное дерево. Суммарная длина ребер равна 
.
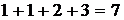Процесс построения минимального остовного дерева изображен ниже.
7.10. Задачи для самостоятельного решения
1. Какое из двух утверждений верно?
а) ориентированный граф является частным случаем неориентированного графа;
б) неориентированный граф является частным случаем ориентированного графа.
2. Что характеризует сумма элементов столбца матрицы смежности неориентированного графа?
3. Что характеризует сумма элементов строки матрицы смежности неориентированного графа?
4. Что характеризует сумма элементов столбца матрицы смежности ориентированного графа?
5. Что характеризует сумма элементов строки матрицы смежности ориентированного графа?
6. Всегда ли матрица смежности симметрична относительно главной диагонали?
7. Как по матрице смежности определить число ребер неориентированного графа?
8. Как по матрице инцидентности, не рисуя граф, определить его матрицу смежности?
9. Какие из следующих утверждений являются правильными?
а) если матрица смежности несимметричная, то граф ориентированный;
б) если граф неориентированный, то матрица смежности симметричная;
в) если диагональные элементы матрицы смежности – нули, то граф неориентированный.
10. Может ли вершина, входящая в цикл графа, иметь степень, меньшую двух?
11. Как называется путь, у которого начало первой дуги совпадает с концом последней?
12. Как называется маршрут, у которого первая вершина совпадает с последней вершиной?
13. Какие из следующих матриц полностью задают граф?
а) матрица инцидентности; б) матрица связности;
в) матрица сильной связности; г) матрица смежности.
14. По какой матрице можно без дополнительных вычислений определить число компонент связности неориентированного графа?
а) матрице смежности; б) матрице инцидентности;
в) матрице связности.
15. Может ли число компонент связности графа превосходить число его вершин?
16. Верно или неверно утверждение, что в ориентированном графе с контурами минимальный путь может содержать контуры?
17. Как называется связный граф без циклов?
18. Сколько ребер имеет связный граф без циклов с вершинами?
19. Чему равно наименьшее и наибольшее число ребер в связном графе без петель и кратных ребер с 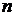вершинами?
20. Чему равно наименьшее и наибольшее число ребер в графе без петель и кратных ребер с 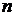вершинами?
21. Верно или неверно утверждение, что минимальное остовное дерево может содержать циклы?
22. Сколько компонент связности может иметь дерево?
23. Можно ли построить дерево, все вершины которого имеют степень больше, чем единица?
24. Может ли матрица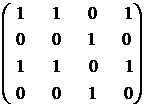 
быть матрицей смежности неориентированного графа?
ЛИТЕРАТУРА
1. Хаусдорф Ф. Теория множеств. – 3-е изд., стер. – М.: КомКнига, 2006.