Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники. Ч.1 Л.: Энергоиздат, 2001.

Примеры выполнения расчёта.

В качестве примера произведем расчет электрической цепи, схема которой приведена на рис. 1.

Параметры

E₁ = 9В; E₂ = 13В; E₃ = 17В;

r₁ = 3 Ом; r₂ = 2 Ом; r₃ = 5 Ом;

r₄ = 7 Ом; r₅ = 6 Ом; r₆ = 10 Ом;

Рис.1 Схема электрической цепи.

I. Составление по законам Кирхгофа системы уравнений для расчета заданной электрической цепи.

Изображаем расчетную схему цепи (рис.2),на которой показываем положительные направления Э.Д.С. и произвольно выбранные положительные направления токов в ветвях, а также направления обходов контуров (по часовой стрелке). Обозначаем узлы цепи буквами А, В, С, Д.

Рис.2. Расчетная схема.

По первому закону Кирхгофа можно составить число уравнений равное q – 1, где q – число узлов. Для данной цепи число уравнений будет 4 – 1 = 3.

Уравнения по первому закону Кирхгофа составляем для узлов А, В, С.

Узел А I₄ – I₅ – I₆ = 0,

Узел В I₆ – I₁ – I₂ = 0,

Узел С I₂ + I₃ – I₄ = 0.

По второму закону Кирхгофа можно составить независимые контурные уравнения, число которых равно n = b – (q-1), где b – число ветвей в цепи. Для данной цепи n = 6- (4-1) = 6-3 = 3.

Уравнения по второму закону Кирхгофа составляем для независимых контуров I,II,III.

Для контура I: r₆ I₆ + r₁ I₁ – r₅ I₅ = E₁.

Для контура II: r₂ I₂ – r₃ I₃ – r₁ I₁ = E₂ – E₃ – E₁.

Для контура III: r₅ I₅ + r₃ I₃ – r₄ I₄ = E₃.

Подставив в уравнения, составленные по первому и второму законам Кирхгофа, значения сопротивления и известных э.д.с., получаем окончательно:

I₄ – I₅ – I₆ = 0, (1)

I₆ – I₁ – I₂ = 0, (2)

I₂ + I₃ – I₄ = 0. (3)

10I₆ + 3I₁ – 6I₅ = 9, (4)

2I₂ – 5I₃ – 3I₁ = -13, (5)

6I₅ + 5I₃ + 7I₄ = 17. (6)

Решение системы из шести уравнений с шестью неизвестными достаточно сложно, поэтому для расчета рассматриваемой электрической цепи применяем другие методы.

2. а) Определение токов во всех ветвях системы методом контурных токов в матричной форме.

1.В данной схеме можно выделить три независимых контура, например, контуры АВДА, ВСДВ, АДСА. Полагаем, что в каждом из этих контуров течет свой контурный ток, соответственно, J₁, J₂, J₃. Уравнения составляем относительно контурных токов, выбираем произвольно (по часовой стрелке).

Расчёт ведём по схеме, приведённой н+а рис.3.

Рис.3. Расчётная схема.

При составлении уравнений в левой части каждого из них стоит произведение контурного тока на сумму всех сопротивлений этого контура плюс произведение соседнего тока на смежное сопротивление (если контурные токи протекают в этом сопротивлении в одном направлении и с минусом, если эти направления противоположны), а в правой - алгебраическая сумма э.д.с. данного контура. Э.д.с, совпадающие с направлением обхода, входят в уравнение с плюсом, направленные против обхода - с минусом.

Составляем уравнения по методу контурных токов для контура АBDA.

для контура BCDB

для контура ADCA

2. Полученную систему трёх уравнений с тремя неизвестными представим в матричной форме

или сокращенно

Это матричное уравнение может быть решено относительно матрицы |J|.

Для этого обе стороны уравнения (2) должны быть умножены на матрицу, обратную матрице |r|.

Квадратная матрица |r| собственных и общих смежных сопротивлений контуров может представлена как где a₁₁=r₁ + r₅ + r₆ ; a₁₂=-r₁ и.т.д. называются элементами матрицы.

Обратная матрица имеет вид

где Δ_r – определитель системы

Для получения обратной матрицы ||r||^-1 необходимо заменить в исходной матрице ||r|| каждый элемент a_ij его алгебраическим дополнением, R_ij, затем заменить строки соответствующими столбцами и полученную таким образом матрицу разделить на определитель исходной матрицы Δ_r.

Алгебраическим дополнением R_ij элемента a_ij квадратной матрицы |r| называется умноженной на (-1)^i+j определитель, получающийся из элементов матрицы ||r|| после исключения i – ой строки и j – го столбца, т.е. R_ij = (-1)^i+j M_ij ,

где M_ij – определитель, получающийся из элементов матрицы ||r||, например,

Произведение обратной матрицы на исходную матрицу равно единичной матрице, т.е. квадратной матрице, у которой все элементы главной диагонали (идущие от левого верхнего угла к правому нижнему) равны единице, а остальные элементы равны нулю

Следовательно

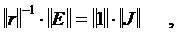
где ||1|| - единичная матрица.

Произведение

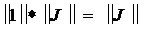,Поэтому

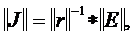или в развёрнутой форме

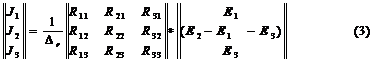
В результате умножения матриц получаются выражения для контурных токов, например

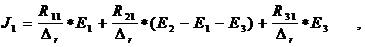
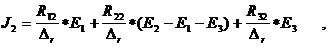
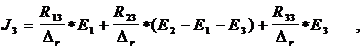
Подставим в систему уравнение в матричной форме ( I ), значения сопротивления и э.д.с.

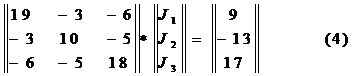
Решаем матричное уравнение (4) относительно матрицы|J|. Определяем определитель системы:

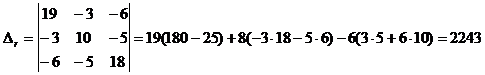
Определяем алгебраические дополнения элементов матрицы

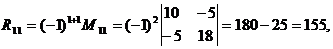
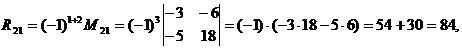
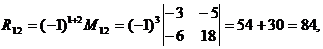
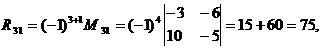
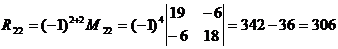
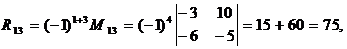
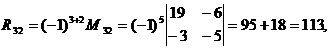
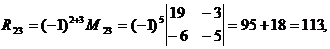
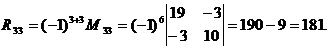
После подстановки вычисленных значений Δ_r и R_ij получаем

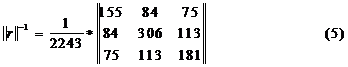
Подставим (5) в (3), получаем окончательно

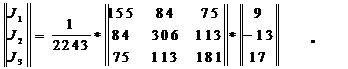
Отсюда

J₁= (1395 – 1092 +1275) /2243 = 1578 / 2243 = 0.704 A.

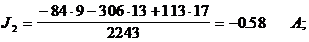
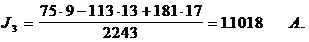
3. Находим действительные токи в ветвях схемы

I₁ = J₁ – J₂ = 0.704 – (-0.58) = 1.284 A;

I₂ = J₂ = -0.58 A:

I₃ = J₃ – J₂ = 1.018 – (-0.58) = 1.598 A;

I₄ = J₃ = 1.018 A:

I₅ = J₃ – J₂ = 1.018 – 0.704 = 0.314 A;

I₆ = J₁ = 0.704 A:

Действительные токи во внешних ветвях равны соответствующим контурным токам, а в смежных ветвях - алгебраической сумме контурных токов, обтекающих рассматриваемые смежные ветви.

В результате расчета ток ?₂ получился отрицательным. Следовательно, действительное его направление обратно указанному.

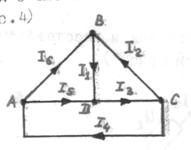На структурной схеме покажем действительные направления всех токов в ветвях (рис.4)

Рис.4. Структурная схема цепи.

4.Проверка правильности определения искомых величин.

Проверка решения производится подсчётом баланса мощностей. Под балансом мощностей понимается равенство мощности, выдаваемой всеми источниками цепи, и мощности, потребленной в сопротивлениях. Баланс мощности основан на законе сохранения энергии.

Мощность, выдаваемая источниками (P_n), подсчитывается по формуле:

P_n = E₁I₁ + E₃I₃ – E₂I₂ = 9•1.284 + 17•1.598 - 13•0.58 = 31.2 Вт.

Если э.д.с. источника и ток через него совпадают по направлению, это значит, что источник энергии выдаёт, и произведение Е•I берется со знаком плюс. Если э.д.с. источника и ток источника встречны, то произведение Е•I берется со знаком минус, источник в этом случае является потребителем.

Мощность потребителей (Рn) подсчитывается по формуле:

Рn = r₁ I²₁ + r₂ I²₂ + r₃ I²₃ + r₄ I²₄ + r₅ I²₅ + r₆ I²₆ = 31,9 Вт.

Погрешность

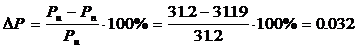
Погрешность ΔР = 0.032, что вполне допустимо (допускается погрешность до3%).

б) Расчет цепи по методу узловых напряжений (потенциалов). Узловыми напряжениями будем называть разность потенциалов между любым узлом электрической цепи и одним из её узлов, принятым за базисный.

Все узловые напряжения указываются на схеме стрелкой к базисному узлу (т.е. он во всех случаях принимается за точку низшего потенциала).

в) Выбираем узел А за базисный и расставляем положительные направления токов и напряжений (рис.5)

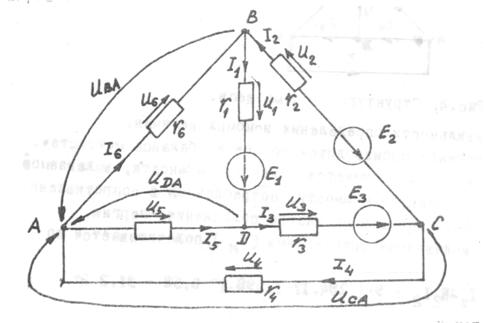
Рис.5 Расчётная схема по методу узловых напряжений.

2. Составляем систему уравнений, содержащих искомые узловые напряжения. Для расчёта схемы методом узловых напряжений можно пользоваться следующим правилом построение уравнений.

В левой части уравнения записывается с плюсом произведение узлового напряжения рассматриваемого узла на арифметическую сумму всех проводимостей ветвей, примыкающих к этому узлу, и с минусом – произведения узловых напряжений соседних узлов на проводимости ветвей, соединяющих эти узлы с тем, для которого составляется уравнение.

В правой части уравнения записывается алгебраическая сумма произведения э.д.с., примыкающих к рассматриваемому узлу, на проводимость своих ветвей, причём перед произведением ставится знак плюс, если стрелка э.д.с. смотрит к узлу, и минус – если она направлена от узла.

Узел В : (g₁+g₂+g₆)U_BA – g₁U_DA – g₂U_CA = -g₁E₁ – g₂E₂ ,

Узел С : (g₂+g₃+g₄)U_CA – g₃U_DA – g₂U_BA = g₂E₂ + g₃E₃ ,

Узел Д : (g₁+g₃+g₅)U_DA – g₁U_DA – g₃U_CA = g₁E₁ – g₃E₃ ,

Подставив в значения э.д.с. и сопротивлений получим:

U_BA (1/3 + 1/2 + 1/10) – 1/3 U_DA – 1/2 U_CA = -(1/3) 9 – (1/2) 13,

- 1/2 U_BA – 1/5 U_DA + (1/5 + 1/2 + 1/7)U_CA = (1/2) 13 + (1/5) 17,

1/3 U_BA + (1/3 + 1/5 + 1/6)U_DA – 1/5 U_CA = (1/3) 9 – (1/5) 17,

Упростив выражение, получим:

14/15 U_BA – 1/3 U_DA – 1/2 U_CA = - 9.5 ,

-1/2 U_BA – 1/5 U_DA + 59/70 U_CA = 9.9 ,

-1/3 U_BA + 21/30 U_DA – 1/5 U_CA = - 0.4 .

Решением уравнений относительно искомых узловых напряжений может быть найдено с помощью определителей.

Определяем определитель системы:

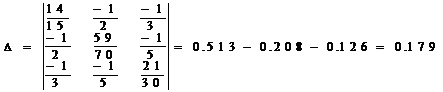
Определяем алгебраические дополнения:

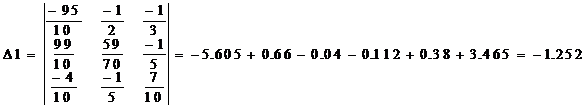
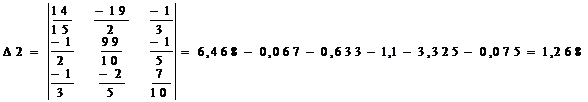
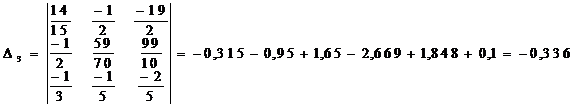
Определяем узловые напряжения:

U_BA = D₁ /D = - 1.252 / 0.179 = 7.0 B ,

U_CA = D₂ /D = 1.268 / 0.179 = 7.084 B ,

U_DA = D₃ /D = - 0.336 / 0.179 = - 1.877 B.

4. Определяем токи в ветвях схемы:

I₁ = (E₁ + U_BA – U_DA) / r₁ = (9 – 7 + 1.877) / 3 = 1.294 A ;

I₂ = (U_CA – U_BA – E₂) / r₂ = (7.084 + 7 - 13) / 2 = 0.549 A.

I₃ = (E₃ – U_CA + U_DA) / r₃ = (17 – 7.084 – 1.877) / 5 = 1.607 A,

I₄ = 7.084 / 7 = 1.012 A,

I₅ = - U_DA / r₅ = 1.877 / 6 = 0.313 A,

I₆ = - U_BA / r₆ = 7 / 10 = 0.7 A.

5.Произведем проверку решения подсчетом балансов мощностей:

P = E₁I₁ + E₃I₃ – E₂I₂ = 9•1.294 + 17•1.607 - 13•0.549 = 31.828 Вт,

P_п = r₁•I₁² + r₂•I₂² + r₃•I₃² + r₄•I₄² + r₅•I₅² + r₆•I₆² =

= 3•1.294² +2•0.549² + 5•1.607² + 7•1.012² + 6•0.313² + 10•0.7² = 31.18 Вт.

Погрешность

DP = (P_n – P_п) 100% / P_n = (31.828 – 31.18) 100% / 31.828 = 2.07 %.

что вполне допустимо.

III. Определение тока в третьей ветви по методу эквивалентного генератора.

Сущность метода эквивалентного генератора заключается в том, что ток в ветви определяется как частное от деления э.д.с., численно равной напряжению между точками присоединения рассматриваемого сопротивления при его отключении (U_хх), на сумму эквивалентного сопротивления всей цепи относительно тех же точек и выделенного сопротивления цепи.

1. Исходная формула для определения тока I₃ в цепи (рис.1) имеет вид:

I₃ = U_X/(r_Э+r₃),

где U_хх – напряжение между точками присоединения рассматриваемого сопротивления при его отключении, r_Э - эквивалентное сопротивление всей цепи относительно точек присоединения рассматриваемого сопротивления r₃).

Из формулы видно, что для определения I₃ нужно знать U_хх и r_Э.

Для определения U_хх нужно составить новую расчетную схему с выключенным сопротивлением r₃ (рис.6)

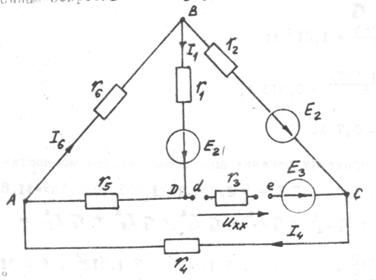
Рис.6 Расчетная схема по методу эквивалентного генератора.

Для нахождения U_хх, токи в ветвях расчетной схемы (рис.6) определяем методом наложения, разбивая её на ряд частичных подсхем (рис.7 а, б.). При этом в каждой подсхеме действует по одной э.д.с.

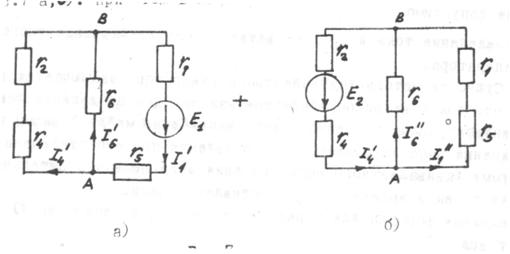
Рис.7

Расчитываем эти подсхемы:

Подсхема а)

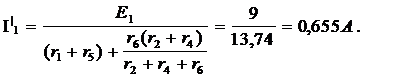
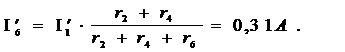
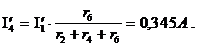
Подсхема б):

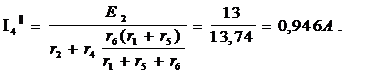
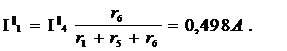
3. Находим действительные токи I₁,I₄,I₆ в схеме на рисунке 6.

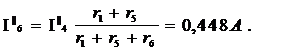
Действительные токи в схеме определяются суммированием частичных токов в ветвях. При суммировании удобно пользоваться следующим правилом.

В уравнении с плюсом записываем те токи подсхем, направление которых совпадает с направлением тока исходной схемы, подставленной на рис. 6:

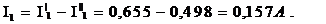
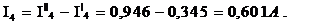
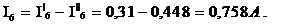
4. Правильность расчёта проверяется составлением баланса мощностей.

P_n = E₁I₁ + E₂I₄ = 9.26 Вт.

Р_п = (r₂ + r₄)I²₄ + r₆ I²₆ + (r₁ + r₅)I²₁ = 9.24 Вт.

Погрешность

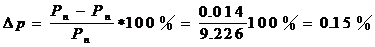
Определяем Uxx между точками разрыва a и e (рис. 6.)

-I₁r₅ + Uxx – E₃ + I₄r₄ = 0

Тогда

Uxx = E₃ + I₁r₅ - I₄r₄ = 13.735 Вт.

6. Определяем сопротивление r_э по схеме цепи (рис.6) относительно разрывов d и e при удалённых из неё э.д.с. источников.

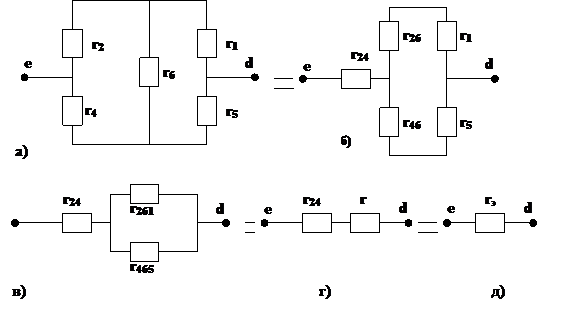Рис. 8

Треугольник сопротивления r₂, r₄, r₆ заменяем эквивалентной трёхлучевой звездой r₂₄, r₂₆, r₄₆ (рис. 8,б)

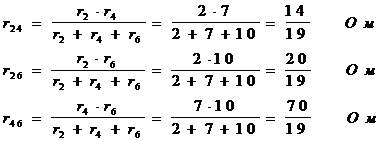
Определяем r_э, свёртывая схему (рис.8 в,г,д)

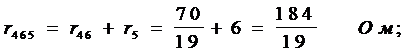
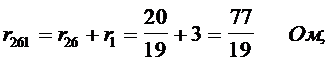
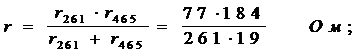
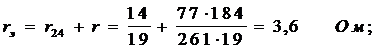
7. По написанной ранее исходной формуле вычисляем ток в третьей ветви.

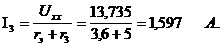
Получено такое же значение тока I₃, как и при расчётах методом контурных токов и узловых напряжений.

8. Нахождение тока в третьей ветви методом сигнальных графов, при допущении в указанной схеме (рис. 1) Е₁=0, Е₂=0.

1. Составляем расчетную схему (рис. 9).

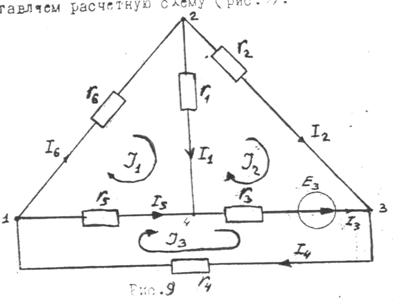
Рис. 9

2. Записываем систему уравнений по методу контурных токов.

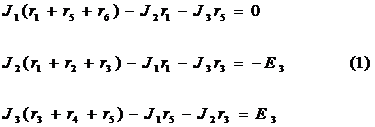
Для построения сигнального графа необходимо разрешить каждое уравнение системы (1) относительно одного неизвестного тока (разных для разных уравнений).

Например, первое уравнение решим относительно J₁, второй относительно J₃, третий относительно J₃.

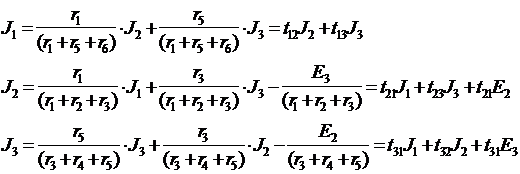
Где

t₁₂ = r₁ / (r₁ + r₅ + r₆) = 3 / (3 + 6 + 10) = 3 / 19 ;

t₂₁ = r₁ / (r₁ + r₂ + r₃) = 3 / (3 + 2 + 5) = 3 / 10 ;

t₃₁ = r₅ / (r₃ + r₄ + r₅) = 6 / (5 + 7 + 6) = 6 / 18 ;

t₁₃ = r₅ / (r₁ + r₅ + r₆) = 6 / (3 + 6 + 10) = 6 / 19 ;

t₂₃ = r₃ / (r₁ + r₂ + r₃) = 5 / (3 + 2 + 5) = 5 / 10 ;

t₃₂ = r₃ / (r₃ + r₄ + r₅) = 5 / (5 + 7 + 6) = 5 / 18 ;

t₂₄ =-1 / (r₁ + r₂ + r₃) = -1 / (3 + 2 + 5) = -1 / 10 ;

t₃₄ = 1 / (r₃ + r₄ + r₅) = 1 / (5 + 7 + 6) = 1 / 18 ; - коэффициенты передачи ветвей.

3. Составление сигнального графа соответствующего системе 2.

Сигнальный граф состоит из узлов и ветвей. Ветвь изображается направленным отрезком, соединяющим 2 узла сигнального графа. Направление ветви указывается стрелкой.

В каждом узле графа имеется сигнал, который определяется от узла по всем ветвям выходящим из него. Под сигналами в электрических цепях понимаются токи, напряжения, э.д.с.

Каждая ветвь графа характеризуется коэффициентом передачи tik. Первый индекс i соответствует номеру узла в который входит ветвь, а второй k – номеру узла из которого она выходит.

На основании вышеизложенного составляем сигнальный граф изображенный на рис. 10.

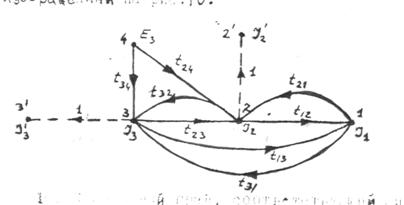
Рис. 10 Сигнальный граф соответствующий системе 2.

Ток J₁ представляет сигнал в вершине (в узле) графа 1, ток J₂ - сигнал в вершине 2, ток J₃ – сигнал в вершине 3, и э.д.с Е₃ – сигнал в вершине 4.

Согласно первому уравнению системы (2) в вершину 1 должна входить ветвь с коэффициентом передачи t₁₂, выходящяя из вершины 2, и ветвь с коэффициентом передачи t₁₃, выходящая из вершины 3 (рис.10).

Сигнальный граф обладает следующими свойствами:

1. При прохождении по ветви сигнал умножается на коэффициент передачи ветви.

2. Результирующий сигнал в узле (вершине) равен сумме всех сигналов, проходящих в данный узел по ветвям, входящий в этот узел.

Так в вершину 2 согласно первому свойству приходят сигналы t₁₂ J₁, t₂₃J₃ и t₂₄E₃, так что результирующий сигнал J₂ в вершине 2 удовлетворяет второму уравнению системы 2.

Аналогичные рассуждения относятся и к остальным ветвям графа на рис.10.

4. Вычисление коэффициентов передач сигнального графа.

Коэффициентом передачи сигнального графа от источника, откуда только выходят ветви графа, к стоку, куда только входят ветви графа называется отношение сигнала в стоке к сигналу в источнике.

Необходимо отметить, что ток в третьей ветви I₃ в схеме равен алгебраической сумме контурных токов J₂ и J₃ (рис.11) т.е. I₃ = J₃ - J₂. Поэтому нам надо найти сигналы в вершинах 3 и 2.

Узел 4 графа на рис.10 является источником, узлы 2 и 3 не являются стоком, но можно добавить узлы 2^² и 3^² и соединить их с узлами 2 и 3, соответственно, ветвями с единичным коэффициентом передач. Тогда J₃^² = J₃ и J₂^² J₂ (рис.10).

Узлы 2^² и 3^² являются стоками, тогда коэффициент передачи от узла 4 к узлу 2^²

Т ₂^² ₄ = J₂^² / E₃ = J₂ / E₃

Если знать передачу графа Т ₂^² ₄ то можно определить ток

J₂ = Т ₂^² ₄• E₃ (3)

Коэффициент передачи от узла 4 узлу 3^²

Т ₃^² ₄ = J₃^² / E₃ = J₃ / E₃

Отсюда

J₃ = Т ₃^² ₄• E₃ (4)

Вычислим коэффициенты передач графа от источника к стоку Т₂^²₄ и Т₃^²₄ по формуле Мейсона.

Т = (å Р_к D_к) / D ; (5)

Где D = 1- å L_i + å L_iL_k - å L_iL_kL_m + ….. определитель графа.

L_i – величина i-го контура, равная произведению коэффициентов передач всех ветвей контура. Контуры выбираются так, чтобы все ветви в контуре были направлены в одну сторону.

Сразу отметим, что å L_iL_k, å L_iL_kL_m и т.д. равны нулю, так как не касающихся контуров в нашем графе нет.

Касающимся контуром, считается контур, составленный из ветвей графа, и имеющий хотя бы общий узел с другим контуром графа. В графе на рис.12 рассматриваемые контуры – касающиеся.

D = 1 - å L_i = 1 – (t₂₃ t₃₂ + t₁₂ t₂₁ + t₁₃ t₃₁ + t₃₂ t₁₃ t₂₁ + t₁₂ t₃₁ t₂₃) =

=1–(5/10•5/8) + (3/19•3/10) + (6/19•6/18) + (5/18•6/19•3/10) + (3/18•6/18•5/10)=

= 1 – (1177/190•18) = 2243/190•18

Р_к – Величина к-го пути в графе от источника до стока. Путь в графе берётся с учетом направления ветвей, т.е. идя от источника до стока, необходимо идти в направлении стрелок. Величина пути равна прпоизведению коэффициентов передач всех ветвей пути.

D_к - алгебраическое дополнение пути. D_к вычисляется по той же формуле, что и определитель графа D, но при этом следует учитывать во всех суммах лишь контуры не касающиеся пути Р_к.

Суммирование å Р_к D_к выполняется по всем возможным путям.

Определяем Р_к и алгебраические дополнения D_к при переходе от источника 4 к стоку 3^².

Путь 1-ый: Р₁ = t₃₄ t₃^²₃ = t₃₄ 1 = 1/18; D₁ = 1-t₁₂ t₂₁ =1-3/19•3/10=181/190.

Путь 2-ой: P₂ = t₂₄ t₁₂ t₃₁ t₃^²₃ = -1/10•3/19•6/18•1 = - 18/(190•18) ; D₂ = 1 .

Путь 3-ий: P₃ = t₂₄ t₃₂ t₃^²₃ = - 1/10•5/18•1 = - 5/180 ; D₃ = 1

Определяем Т₃^²₄ согласно (5)

Т₃^²₄ = (Р₁D₁ + Р₂D₂ + Р₃D₃) / D = (181-18-90) / 2243 = 73 ./ 2243

Определяем Р_к и алгебраические дополнения D_к при переходе от источника 4 к стоку 2^².

Путь 1-ый: Р₁ = t₂₄ t₂^²₄ = t₂₄ 1 = -1/10; D₁ = 1-t₁₃ t₃₁ =1-6/19•6/18=306/(19•18)

Путь 2-ой: P₂ = t₃₄ t₂₃ t₂^²₄ = 1/18•5/10•1 = 5/180 ; D₂ = 1 .

Путь 3-ий: P₃ = t₃₄ t₁₃ t₂^²₄ t₂₁ = 1/18•5/19•3/10 • Т₂^²₄ 1= 18/(190•18); D₃ = 1

Определяем Т₂^²₄ согласно (5) :

Т₂^²₄ = (Р₁D₁ + Р₂D₂ + Р₃D₃) / D = (- 306 + 95 + 18) / 2243 = - 193 / 2243 .

5. Определяем контурные токи J₂ и J₃ согласно (3) и (4)

J₂ = Т₂^²₄ •Е₃ = (- 193•17) / 2243 = -1.467 А;

J₃ = Т₃^²₄ •Е₃ = ( 73•17) / 2243 = 0.553 А;

6. Определяем действительный ток I₃ в третьей ветви

I₃ = J₃ – J₂ = 0.553 + 1.467 = 2.0 A

7. Сделаем проверку правильности найденного тока I₃. С этой целью найдем эквивалентное сопротивление r_э относительно узлов 3 и 4 (рис.9). Искомое сопротивление r_э вычислено в методе эквивалентного генератора относительно точек е и d (рис. 8):

r_э = 3.6 Ом

В результате получаем эквивалентную схему (рис.11).

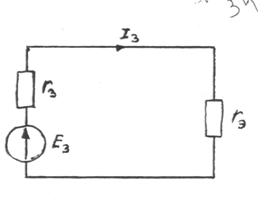
Рис.11

из которой находим ток I₃.

I₃ = E₃ / (r₃ + r_э) = 17 / (5 + 3.6) = 1.98 A.

Погрешность

Δр = (2 – 1.98) 100% / 1.98 = 1%, что допустимо (допускается 3%)

V. Построение потенциальной диаграммы для одного из контуров схемы, например, ДВС (рис.12)

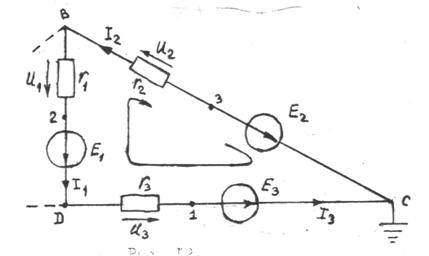
Рис.12

Положительные направления токов в ветвях проставляем в соответствии со схемой представленной на рис.4. Возьмем значения токов, полученных по методу контурных токов.

Потенциальной диаграммой называется график распределения потенциала вдоль какого-либо замкнутого контура или участка цепи.

1. Принимаем потенциал любой точки схемы, например, С, равным нулю (т.е. считаем

её заземленным) и находим потенциалы точек 1,Д, 2, В, 3.

j_С = 0,

j₁ = j_С – Е₃ = 0 – 17 = -17 В,

j_D = j₁ + U₃ = j₁ + r₃ I₃ = -17 + 1.598•5 = 9 B.

j₂ = j_D – E₁ = -9 – 9 = -18

j_B = j₂ + U₁ = j₂ + r₁I₁= -18 + 1.284 •3 = -14.158 B

j₃ = j_B + U₂ = j_B + r₂I₂= -14.158 + 0.58 •2 = -12.998 B

j_C = j₃ + E₂ = -12.998 + 13 = 0

2. Строим потенциальную диаграмму цепи (рис.13). Построение ведем от точки С, движение производим по часовой стрелке.

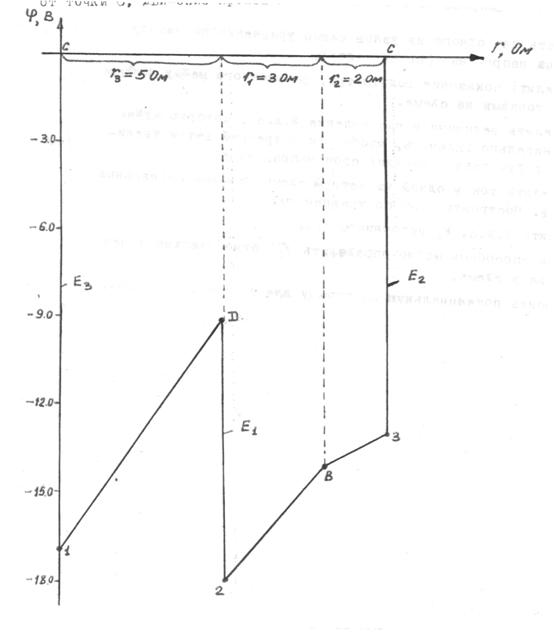
Рис.13 Потенциальная диаграмма.

Потенциальная диаграмма позволяет найти графическим путем разность потенциалов между любыми двумя точками схемы.

Вопросы по расчету при защите.

1. Написать для одного из узлов схемы уравнение по методу узловых напряжений.

2. Определить показания вольтметра, включенного между любыми двумя точками на схеме.

3. Определить величину и направление э.д.с, которую нужно дополнительно включить, чтобы ток в третьей ветви увеличился в два раза и изменил свое направление.

4. Определить ток в одной из ветвей схемы методом сигнальных графов. Построить граф по уравнениям.

5. Заменить э.д.с. Е₄ источником тока.

6. Какими способами можно определить r_э относительно точек разрыва в схеме.

7. Построить потенциальную диаграмму для заданного контура.

8.