Переходные процессы. Определение постоянных интегрирования
Как известно, постоянные интегрирования определяются из начальных условий, каковыми являются значения искомой функции и ее производных по (n – 1)-ую включительно в начальный момент времени 0+ («справа»). В отличие от чисто математических задач, где эти условия задаются в качестве исходных данных непосредственно, при анализе переходных процессов задаются начальные условия «слева» в момент t = 0–, предшествующий коммутации (чаще всего они формулируются самой постановкой задачи и легко определяются из расчета докоммутационного режима). Нахождение начальных условий «справа» по известным значениям начальных условий «слева» – ключевой момент в расчете переходных процессов.
Опишем процедуру отыскания начальных условий в цепи n-го порядка
· для послекоммутационной схемы (  ) составляют систему уравнений для мгновенных значений токов и напряжений по законам Кирхгофа, дополняют эту систему компонентными уравнениями типа
) составляют систему уравнений для мгновенных значений токов и напряжений по законам Кирхгофа, дополняют эту систему компонентными уравнениями типа 
 для емкости;
для емкости; 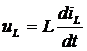 для индуктивности;
для индуктивности;
· рассматривают эту систему уравнений в момент t = 0+ с учетом независимых начальных условий, которые по правилам коммутации берутся равными начальным условиям «слева», в результате определяются зависимые начальные условия, в том числе значения первых производных от индуктивных токов и емкостных напряжений;
· для отыскания значений первых производных от зависимых электрических величин и вторых производных от независимых электрических величин необходимо систему уравнений из п. 1 продифференцировать и рассмотреть ее в момент t = 0+ с учетом информации, полученной в п. 2;
· процедура дифференцирования продолжается до тех пор, пока не будет найдена (n – 1)-ая производная искомой функции в 0+.
Система уравнений для определения постоянных интегрирования имеет следующий вид:
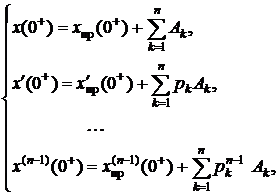 (4.9)
(4.9)
Здесь для определенности полагаем все корни pk вещественными разными числами. Кроме того, следует учитывать, что при наличии в цепи только источников постоянных воздействий значение производных от принужденной составляющей переходного процесса равны нулю.
Возможная схемная реализация этой технологии подробно описана в [] и позже будет пояснена на конкретном примере.
 17. Переходные процессы. Разряд заряженной ёмкости через сопротивлениеR
17. Переходные процессы. Разряд заряженной ёмкости через сопротивлениеR
1. Запишем правило коммутации для цепи на рис. 4.5:
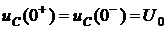 .
.
2. Составим дифференциальное уравнение цепи:
 ;
;
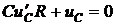 .
.
Характеристическое уравнение первого порядка:
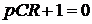 ,корень которого
,корень которого  .
.
3. Полное решение дифференциального уравнения:
 .
.
Поскольку уравнение имеет первый порядок, свободная составляющая имеет одну экспоненту 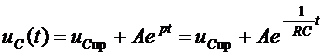 .
.
4. Определим принужденную составляющую 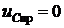 .
.
5. Для определения постоянной интегрирования A запишем полное решение для момента t = 0+
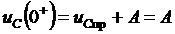 .
.
Применив правило коммутации, получим окончательное решение
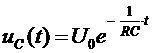 .
.
Ток в цепи определяется с помощью дифференциального закона Ома
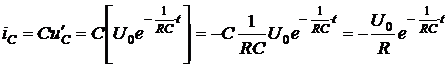 ,
,
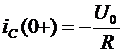 ,
,  .
.
Итак, имеем две экспоненты, описывающие изменения  и
и  . Графики изменения
. Графики изменения  и
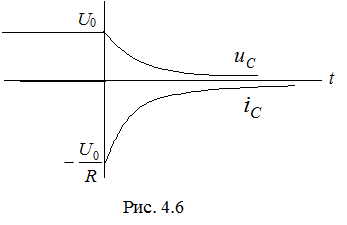
и  представлены на рис. 4.6. Напряжение на конденсаторе непрерывно в момент коммутации и уменьшается по экспоненциальному закону от начального значения U0. Знак «минус» в выражении для тока говорит о том, что ток при разряде конденсатора направлен противоположно току при его заряде. В начальный момент значение тока максимально, его спад связан с уменьшением напряжения на элементах цепи. Ток на ёмкости меняется скачком.
представлены на рис. 4.6. Напряжение на конденсаторе непрерывно в момент коммутации и уменьшается по экспоненциальному закону от начального значения U0. Знак «минус» в выражении для тока говорит о том, что ток при разряде конденсатора направлен противоположно току при его заряде. В начальный момент значение тока максимально, его спад связан с уменьшением напряжения на элементах цепи. Ток на ёмкости меняется скачком.
 Введём величину, характеризующую скорость изменения электрической величины в переходном режиме, называемую постоянная времени (t).
Введём величину, характеризующую скорость изменения электрической величины в переходном режиме, называемую постоянная времени (t).
Величина 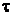 показывает, за какой промежуток времени свободная составляющая переходного процесса уменьшается в
показывает, за какой промежуток времени свободная составляющая переходного процесса уменьшается в  раз.
раз.

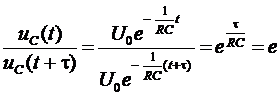 Чем больше
Чем больше 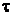 , тем медленнее переходный процесс, тем больше
, тем медленнее переходный процесс, тем больше 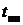 . Хотя полученные выше выражения определяют бесконечную длительность переходного процесса – свободные составляющие лишь асимптотически стремятся к нулю – практически можно считать, что переходный процесс заканчивается за время, равное
. Хотя полученные выше выражения определяют бесконечную длительность переходного процесса – свободные составляющие лишь асимптотически стремятся к нулю – практически можно считать, что переходный процесс заканчивается за время, равное 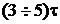 .
.
Постоянную времени можно графически определить по длине подкасательной, проведённой в любой точке свободной составляющей переходного процесса (рис. 4.7).
Постоянная времени измеряется в секундах и для цепей первого порядка связана с корнем характеристического уравнения 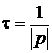 . (4.10)
. (4.10)
Рассмотрим энергетические соотношения, описывающие работу цепи после коммутации.
Энергия электрического поля конденсатора до коммутации –  , в результате полного разряда при
, в результате полного разряда при 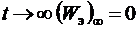 .
.
Покажем, что вся энергия, запасенная в конденсаторе, выделяется в виде тепловой энергии на резисторе R:
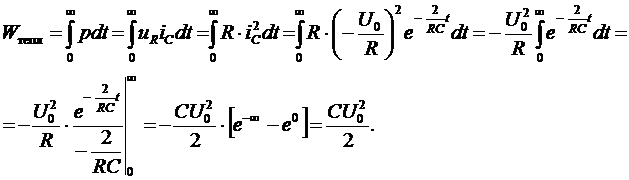
18. Переходные процессы. ПодключениеR  -цепи к источнику постоянного напряжения
-цепи к источнику постоянного напряжения
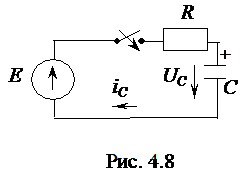 1. Запишем правило коммутации для цепи на рис. 4.8
1. Запишем правило коммутации для цепи на рис. 4.8
 .
.
2. Получим дифференциальное уравнение цепи
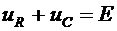
 ,
,
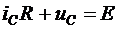 ,
, 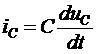 ,
,
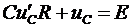 .
.
Характеристическое уравнение цепи
 ,
,
корень которого
 .
.
Постоянная времени  .
.
3. Запишем полное решение 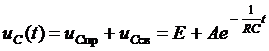 .
.
Здесь свободная составляющая также включает только одну экспоненту, поскольку цепь имеет первый порядок.
 4. Подставив в полное решение t = 0+, определим постоянную интегрирования на основании правил коммутации
4. Подставив в полное решение t = 0+, определим постоянную интегрирования на основании правил коммутации 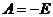 .
.
Таким образом, окончательный результат имеет вид
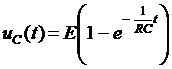 .
.
Ток в цепи
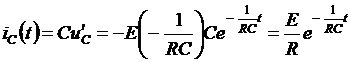 .
.
Графики изменения 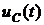 и
и 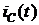 представлены на рис. 4.9. Значение тока, содержащее лишь свободную составляющую, максимально в начальный момент времени, когда оно скачком достигает значение
представлены на рис. 4.9. Значение тока, содержащее лишь свободную составляющую, максимально в начальный момент времени, когда оно скачком достигает значение  , и все напряжение источника приложено к резистору. По мере зарядки конденсатора напряжение на нем повышается, что ведет к соответственному уменьшению тока в цепи.
, и все напряжение источника приложено к резистору. По мере зарядки конденсатора напряжение на нем повышается, что ведет к соответственному уменьшению тока в цепи.
19. Переходные процессы. Подключение R  -цепи к источнику постоянного напряжения
-цепи к источнику постоянного напряжения
1. Запишем правило коммутации для цепи на рис. 4.10
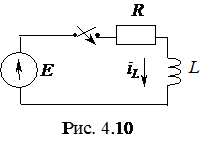
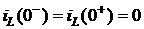 .
.
2. Получим дифференциальное уравнение цепи
 ,
,
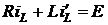 ,
,
характеристическое уравнение
 .
.
Корень характеристического уравнения и постоянная времени соответственно
 ,
,  .
.
3. Полное решение имеет вид:
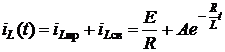 .
.
4. Подставив в iL(t) t = 0+ на основании правила коммутации определим постоянную интегрирования
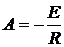 .
.
Таким образом,
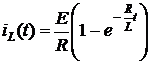 .
.
Напряжение на индуктивности
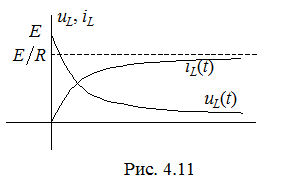
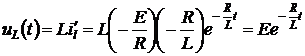 . Графики изменения uL(t), iL(t) приведены на рис. 4.11.
. Графики изменения uL(t), iL(t) приведены на рис. 4.11.
 4.2.5.4. Подключение RC-цепи к источнику гармонического напряжения
4.2.5.4. Подключение RC-цепи к источнику гармонического напряжения
Рассмотрим случай, когда в цепи (рис. 4.12) действует источник синусоидальной ЭДС
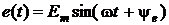 .
.
Здесь 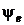 – фаза включения, т.к. она определяется моментом срабатывания коммутатора. Интуитивно следует ожидать влияние
– фаза включения, т.к. она определяется моментом срабатывания коммутатора. Интуитивно следует ожидать влияние 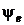 на качественную и количественную картину протекания переходного процесса.
на качественную и количественную картину протекания переходного процесса.
Порядок расчета переходных процессов, описанный выше, не претерпевает никаких изменений.
1. Запишем правило коммутации
 .
.
2. Дифференциальное уравнение и соответствующее ему характеристическое уравнение:
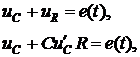
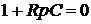 .
.
Корень характеристического уравнения
 .
.
3. Полное решение для рассматриваемой цепи первого порядка
 .
.
4. Расчет принужденной составляющей произведем символическим методом
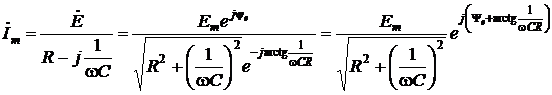 ;
;
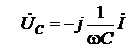 ;
;
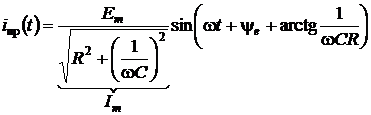 ;
;

 .
.
5. Для расчета постоянной интегрирования запишем полное решение для момента t = 0+
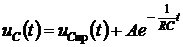 ;
;
 .
.
В соответствии с правилом коммутации
 ;
;
Таким образом,

или
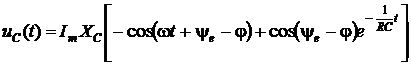 .
.
Определим
 ;
;

Оба выражения для uC и iC в общем случае имеют периодическую принужденную и апериодическую свободную составляющие. При этом характер переходного процесса существенно зависит от двух факторов – начальной фазы напряжения источника в момент включения 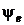 и соотношения параметров цепи
и соотношения параметров цепи 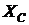 и R.
и R.
Исследуем ожидаемое влияние фазы включения 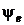 источника на переходный режим
источника на переходный режим
1) Пусть  , тогда
, тогда 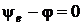 . Поскольку cos 0 = 1, получим
. Поскольку cos 0 = 1, получим
. 
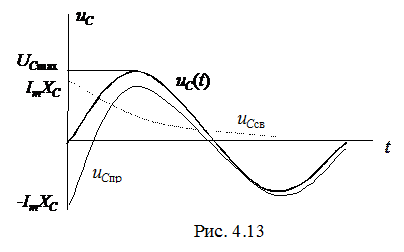
а) исследование кривой напряжения (рис. 4.13) наглядно демонстрирует, что максимальное напряжение в переходном режиме ограничено 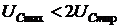 .
.
б) исследование кривой тока (рис. 4.14).
Максимальное значение тока в переходном режиме зависит от соотношения 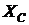 и R и может превышать Imпр в несколько раз. Однако этот начальный всплеск тока является кратковременным.
и R и может превышать Imпр в несколько раз. Однако этот начальный всплеск тока является кратковременным.
 |
2) В случае, если
 , поскольку
, поскольку 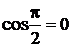 , получим
, получим 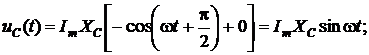
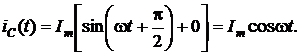
 |
Таким образом, в данном случае в цепи переходный процесс не н
