Геометрическое распределение.

Дискретная случайная величина X имеет геометрическое распределение, если вероятности ее возможных значений 0,1,….,k,.. определяются так:

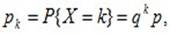
где p – параметр распределения, 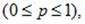а q=1-p.

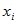				…	k	…
	p			…		…

На практике геометрическое распределение появляется при следующих условиях. Пусть производится некоторый опыт, в котором некоторое событие появляется с вероятностью p. Опыты производятся последовательно, до наступления события. Случайная величина X, равная числу неудачных опытов, имеет геометрическое распределение.

Числовые характеристики геометрического распределения:

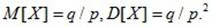
Распределения непрерывных случайных величин. Равномерное, показательное, нормальное..

Равномерное распределение случайной величины.

Непрерывная случайная величина Х равномерно распределена в интервале [а; в], если ее плотность вероятности в этом интервале постоянна, т.е. если все значения в этом интервале равновероятны:

(8.1)

Значение постоянной с определяется из условия нормировки:

. (8.2)

Функция распределения:

, (8.3)

Числовые характеристики равномерно распределенной случайной величины определяются так:

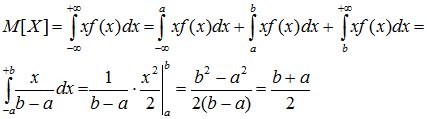(8.4)

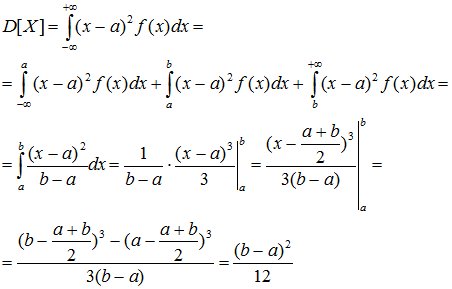(8.5)

Среднее квадратичное отклонение равномерного распределения равно

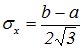(8.6)

Равномерное распределение случайной величины полностью определяется двумя параметрами: a и b – интервалом, на котором определена случайная величина.

При необходимости можно определить параметры a и b равномерного распределения по известным значениям математического ожидания m_X и дисперсии D_X случайной величины. Для этого составляется система уравнений следующего вида:

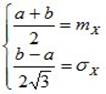, (8.7)

из которой определяются искомые параметры.

Вероятность попадания равномерно распределенной случайной величины в интервал [α,β) определяется так:

, где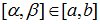

Нормальное распределение

Непрерывная случайная величина Х имеет нормальное распределение, если ее плотность вероятности имеет вид:

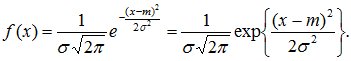(8.12)

Определим числовые характеристики нормально распределенной случайной величины Х. Математическое ожидание:

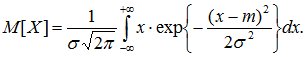
Применяя замену переменной

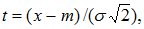(8.13)

получим

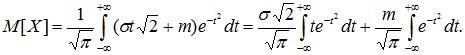
В полученном выражении первый интеграл равен нулю (интеграл в симметричных пределах от нечетной функции), а второй интеграл есть интеграл Эйлера-Пуассона:

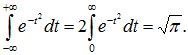(8.14)

Таким образом, математическое ожидание величины Х равно m:

M[X]=m.

Вычислим дисперсию СВ Х:

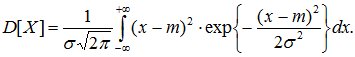
Применяя замену переменной (8.13) получим:

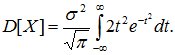
Интегрируя по частям, получим:

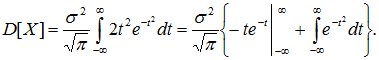
Первое слагаемое в фигурных скобках равно нулю (т.к. 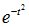при t→∞ убывает быстрее, чем возрастает любая степень t), второе слагаемое, согласно (8.14), равно 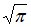, откуда

.

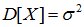Таким образом, нормальное распределение случайной величины полностью описывается двумя числовыми характеристиками: математическим ожиданием M[X] и средним квадратичным отклонением σ.

Рассмотрим влияние параметров m и σ на кривую распределения. При изменении параметра m кривая f(x), не изменяя формы, будет смещаться вдоль оси абсцисс. Изменение σ равносильно изменению масштаба кривой по обеим осям; например, при удвоении σ масштаб по оси абсцисс удвоится, а по оси ординат уменьшится в два раза (рис. 8.3).

Центральные моменты нечетной степени для нормально распределенной случайной величины определяются равны нуню; для вычисления центральных моментов четной степени используется рекуррентное соотношение следующего вида:

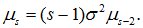(8.15)

Определим вероятность попадания нормально распределенной случайной величины в интервал от α до β:

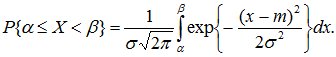
Сделав замену переменной t=(x-m)/σ, получим:

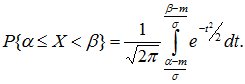
Так как первообразная для e^-x не выражается через элементарные функции, то для вычисления вероятностей событий, связанных с нормальными случайными величинами используют табулированную функцию Лапласа:

.

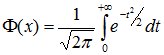С помощью этой функции вероятность попадания нормально распределенной случайной величины на интервал от α до β определится так:

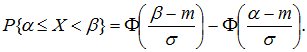(8.16)

Функция Лапласа обладает следующими свойствами:

1. Φ(0)=0;

2. Φ(-х)=-Φ(х);

3. Φ(-∞)=0,5.

Функция распределения нормально распределенной случайной величины через функцию Лапласа выражается так:

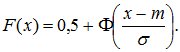(8.16)

Нормально распределенная случайная величина возникает в тех случаях, когда складывается много независимых (или слабо зависимых) случайных величин Х₁, Х₂, …, X_n. Тогда, каковы бы не были законы распределения отдельных случайных величин X_i, закон распределения их суммы будет близок к нормальному распределению. В частности, ошибки измерений распределяются по закону, близкому к нормальному.

показательное распределение — абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события.

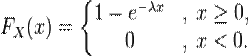
Случайная величина Х называется непрерывной, если ее функция распределения F(x) есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.

Так как для таких случайных величин функция F(x) нигде не имеет скачков, то вероятность любого отдельного значения непрерывной случайной величины равна нулю

P{X=α}=0 для любого α.

В качестве закона распределения, имеющего смысл только для непрерывных случайных величин существует понятие плотности распределения или плотности вероятности.

Вероятность попадания непрерывной случайной величины X на участок от x до x+Dx равна приращению функции распределения на этом участке:

P{x£ X <x+Dx}=F(x+Dx) - F(x).

Плотность вероятности на этом участке определяется отношением

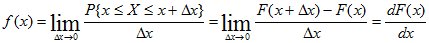(5.6)

Плотностью распределения (или плотностью вероятности) непрерывной случайной величины X в точке x называется производная ее функции распределения в этой точке и обозначается f(x). График плотности распределения называется кривой распределения.

Пусть имеется точка x и прилегающий к ней отрезок dx. Вероятность попадания случайной величины X на этот интервал равна f(x)dx. Эта величина называется элементом вероятности.

Вероятность попадания случайной величины X на произвольный участок [a, b[ равна сумме элементарных вероятностей на этом участке:

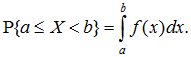(5.7)

В геометрической интерпретации P{α≤X<β} равна площади, ограниченной сверху кривой плотности распределения f(x) и опирающейся на участок (α,β) (рис. 5.4).

Это соотношение позволяет выразить функцию распределения F(x) случайной величины X через ее плотность:

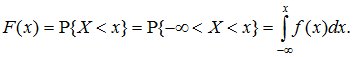(5.8)

В геометрической интерпретации F(x) равна площади, ограниченной сверху кривой плотности распределения f(x) и лежащей левее точки x (рис. 5.5).

Основные свойства плотности распределения:

1. Плотность распределения неотрицательна: f(x) ³ 0.

Это свойство следует из определения f(x) – производная неубывающей функции не может быть отрицательной.

2. Условие нормировки: 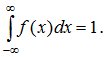Это свойство следует из формулы (5.8), если положить в ней x=∞.

Геометрически основные свойства плотности f(x) интерпретируются так:

1. вся кривая распределения лежит не ниже оси абсцисс;

2. полная площадь, ограниченная кривой распределения и осью абсцисс, равна единице.