Критическая область и критическое значение

Пусть 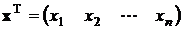– выборка, изъятая из генеральной совокупностиX, плотность распределения которой 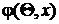. Для проверки гипотезы против вычисляется некоторая функция от выборочных значений 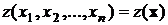, вид которой определяется характером проверяемой гипотезы и параметром (характеристикой), относительно которого выдвигается гипотеза.

Область определения этой функции – все значения, которые образуют генеральную совокупностьX.

Область значений функции 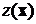Z :{ 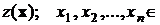X} делится на два непересекающихся множества 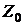и так, что , .

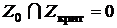Обычно областью определения функции 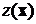является вся вещественная ось, или непрерывный ее отрезок, а каждая из областе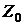й и 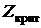– непрерывные части этого отрезка, разделенные точкой или третьим непрерывным отрезком. Точка, разделяющая эти области отображает на оси критическое значение, которое обозначается, как 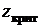. Совокупность функции 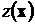и множеств 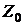, называется критерием проверки гипотезы против , функция 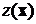– статистика критерия, множество – критическая область или критическое множество. Понятно, что будучи функцией от выборочных данных, статистика критерия является случайной функцией.

выбирается так, чтобы при предположении о справедливости гипотезы условная вероятность попадания статистики критерия в критическую область 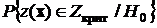была небольшой.

Если оказалось, что при выдвинутом предположении о справедливости гипотезы 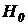и небольшой заранее назначенной вероятности статистика критерия попала в критическую область, что соответствует вероятности 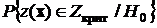, то делается вывод о том, что, повидимому, экспериментальные данные не подтверждают справедливость нулевой гипотезы. В этой ситуации говорят, что нет достаточных оснований для признания справедливости гипотезы . В противном случае, когда статистика критерия попала в область 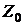, говорят, что нет достаточных оснований для отклонения гипотезы . Однако, из-за действия случайных факторов, особенно, если объем выборки недостаточен, возможны ошибки в таких суждениях, и вероятности этих ошибок необходимо, по крайней мере, знать.

В теории и практике статистических методов проверки гипотез используются следующие определения и понятия:

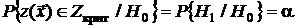– вероятность ошибки первого рода, или риск поставщика, или риск продавца, или уровень значимости, (может применяться любой из этих терминов применительно к конкретной ситуации),

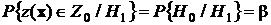– вероятность ошибки второго рода, или риск заказчика, или риск покупателя.

Естественно, что

,

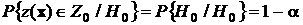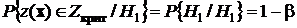– называется мощностью критерия проверки гипотез.

Вероятность a + 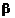есть вероятность ошибки.

Вероятности αи 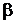обычно выбираются в каждом конкретном случае из экономических или технических соображений, а также из соображений безопасности.

Приведем пример. При контроле выпускаемых изделий и действии случайных факторов вероятность aесть не что иное, как относительное количество годных изделий, ошибочно забракованных и направленных на утилизацию, или на дополнительную регулировку, или в ремонт. Ущерб производителя складывается из напрасно затраченных средств на изготовление, ремонт, регулировку изделия и нереализованной прибыли от его реализации.

Вероятность 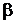– это не что иное, как относительное количество дефектных изделий, ошибочно выпущенных на реализацию, как годные. Потребитель, если он не предъявил рекламацию, несет прямой ущерб. Если же потребитель предъявил рекламацию, то ущерб несет производитель в размере затрат на транспортировку, ремонт, регулировку изделия, и кроме того производитель несет ущерб от утраты положительной репутации на рынке подобных изделий.

Простые гипотезы

Простой называется гипотеза о значении числовой характеристики или параметра, когда область значений, предполагаемых этой гипотезой, и область альтернативных значений - каждая из них являются одноточечной.

В других случаях гипотеза называется сложной.

Пример простой гипотезы.

Плотность распределения генеральной совокупности – нормальна, дисперсия известна и равна 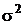. Из генеральной совокупности X извлечена выборка 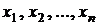. Проверяется простая гипотеза

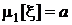: против альтернативы : .

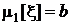Примеры необходимости проверки подобного рода гипотез в технике:

при цифровой передаче данных в условиях действия сильных помех с целью различения передаваемых двоичных символов 0 и 1;

в системах управления технологическими процессами с целью выявления состояния двухпозиционных устройств, контроля исполнения дискретных управляющих воздействий, обнаружения разладки технологического процесса и т.д.

Для проверки этой гипотезы подходящей статистикой является среднее арифметическое значение, плотность распределения которого, как мы уже выяснили, также нормальна с дисперсией 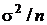, а математическое ожидание равно a или b – в зависимости от того, какая из двух гипотез реально имеет место.

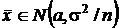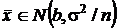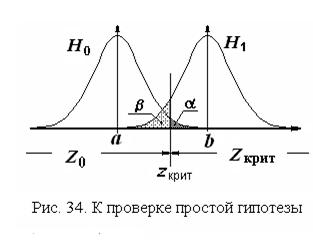
В случае справедливости гипотезы , в случае справедливости гипотезы . Эти две плотности распределения статистики 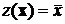приведены на рис. 34. Они пересекаются, и стоит задача определения границы областе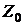й и , то есть критического значения 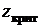, чтобы обеспечить требуемые значения вероятностей ошибочных решений a и b. Эти вероятности показаны на рис.34, как площади под кривыми плотностей распределения статистики, соответствующих гипотезам и .

В самом деле, если гипотеза справедлива, среднее арифметическое значение из-за действия случайных факторов может попасть в критическую область с вероятностью 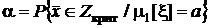. Тогда, если так случится, будет сделан ошибочный вывод, который приведет к отклонению этой, на самом деле справедливой гипотезы.

В противном случае, когда справедлива гипотеза , среднее арифметическое значение из-за действия случайных факторов может попасть в область 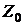с вероятностью 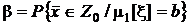, что также приведет к ошибочному выводу.

Видно (см. рис. 34), что перемещением границы между областям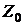и и 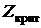можно устанавливать желательное соотношение между вероятностями a и b. Но может оказаться, что их значения слишком велики, и перемещение критического значения не приводит к их снижению. В таком случае необходимо увеличивать объем выборки. В результате дисперсия среднего арифметического уменьшится, его плотность распределения сузится, общая площадь под обеими кривыми уменьшится и, следовательно, уменьшатся вероятности ошибочных решений.

Этот пример показывает, что при проверке простой гипотезы контролируются значения обеих вероятностей ошибочных решений: a и b.

Сложные гипотезы

Пример сложной гипотезы. Плотность распределения генеральной совокупности нормальная, дисперсия известна и равна 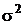. Из генеральной совокупности X извлечена выборка 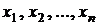. Проверяется сложная гипотеза

: против альтернативы : .

Примеры необходимости проверки подобного рода гипотез:

выявление разладки технологического процесса по параметру a;

распознавание перехода значения регулируемого параметра через уставку;

выявление превышения некоторой характеристикой установленной нормы (при медицинской диагностике, экологическом мониторинге, контроле качества пищевых продуктов, при сертификационных и иных испытаниях изделий и т.д.).

Поскольку проверяются гипотезы о математическом ожидании, как и в предыдущем разделе, подходящей статистикой для проверки этой гипотезы является среднее арифметическое, плотность распределения которого нормальна с дисперсией .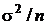

На рис. 35 приведены примеры двух вариантов расположения плотностей распределения средних арифметических значений, соответствующих гипотезам и : при значительном удалении друг от друга истинных значений математических ожиданий (см. рис. 35, а) и при близком их расположении.

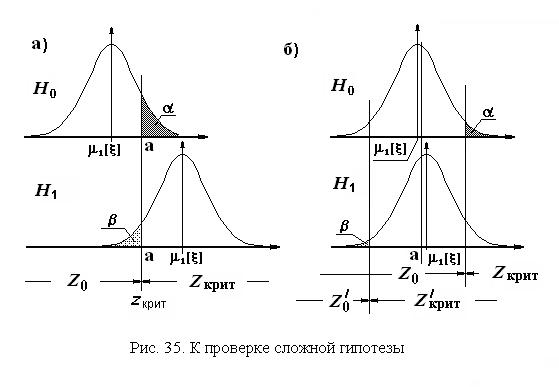
Если в первом варианте в качестве критического значения выбрать значение а, и сравнивать с ним получающееся среднее арифметическое значение, то возможно достижение достаточно малых значений вероятностей ошибочных решений a и b. Однако, формулировка сложной гипотезы допускает вариант, показанный на рис. 35, б. В этой ситуации, если критическим значением является а, вероятности a и bсколь угодно близки к 0,5, что для практики недопустимо. Можно уменьшить вероятность ошибки первого рода aпутем перемещения границы между областями и вправо. 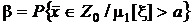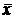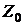Но тогда вероятность ошибки второго рода будет недопустимо близка к единице, поскольку в этом случае она равна площади под кривой плотности распределения статистики , соответствующей гипотезе , по всей области ,то есть области, при попадании 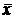в которую принимается решение о непротиворечивости экспериментальным данным гипотезы .

Попытка уменьшить значение вероятности b путем перемещения влево критического значения, то есть границы между областям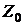и и (на рис. 35 эти области обозначены, как 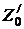и ), приводит к недопустимо близкому к единице значению вероятности ошибки первого рода .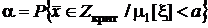

Из этого следует, что при проверке сложных гипотез может контролироваться только одна из вероятностей ошибочного решения: либо a, либо b. Значение другой из них не гарантируется и может быть сколь угодно близким к единице.

Это обстоятельство является существенным недостатком описанного метода проверки сложных гипотез.