Выполняемого с целью полиномиальной аппроксимации

Снова обратимся к конструкции матрицы X, приведенной в разд. 2.3.7.2, и к одной из формул вычисления ковариационной матрицы оценок коэффициентов полинома, например, 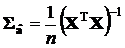. Из конструкции матрицы X видно, что ее элементы изменяют свои значения в зависимости от значений аргумента полинома: 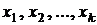. Стало быть, можно надеяться на то, что существует такой план расстановки этих значений, при котором погрешности в каком-либо смысле будут минимальными.

Такие планы, действительно, существуют. Назовем некоторые из них (см., например, [15]).

А-оптимальный план эксперимента – план, при котором достигается минимум следа матрицы 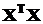, то есть минимум суммы ее диагональных элементов.

D-оптимальный план эксперимента – план, при котором достигается минимальное значение определителя матрицы .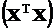

С-оптимальный план эксперимента – план, при котором достигается минимальное значение числа обусловленности матрицы .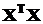

С-оптимальный план эквивалентен D-оптимальному плану.

2.3.7.9. Расширение класса аппроксимирующих полиномов

Материал, изложенный выше в разд. 2.3.7.1 – 2.3.7.8, в равной степени относится к оценке коэффициентов обобщенных аппроксимирующих полиномов с заменой понятия “степень полинома” на “порядок полинома”.

Обобщенным полиномом называется полином вида

,

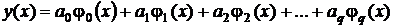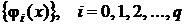– система базисных функций.

Если эти функции ортогональны и соответствуют характеру аппрокси­мируемой зависимости лучше, чем степени x, то для достижения необходимой точности аппроксимации может понадобиться меньше членов, чем в случае аппроксимации степенным полиномом. А это обстоятельство способствует улучшению обусловленности задачи и является четвертым средством повышения устойчивости оценок МНК и ОМНК.

Матрица X в этом случае будет иметь следующую конструкцию:

.

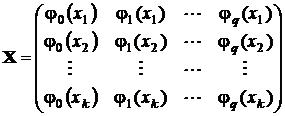Это единственное отличие от изложенного ранее в данном разделе. Все остальные формулы, замечания и рекомендации остаются в силе без каких-либо изменений.

ИНТЕРВАЛЬНОЕ ОЦЕНИВАНИЕ

Постановка задачи

Как и ранее, будем обозначать генеральные значения моментов, или параметров плотности распределения, или иные характеристики генеральной совокупности случайной величины Q.

Точечные оценки генеральных характеристик (параметров) Qнедостаточно информативны, поскольку в них не содержится сведений о том, насколько далеки они от истинных значений. Напротив, интервальные оценки содержат такие сведения.

Целью интервального оценивания является вычисление по выборочным данным х объема n такого интервала с границами: нижней 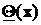и верхней 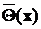, чтобы

,

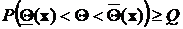где Q – вероятность, близкая к единице, например Q=0,8 – 0,95.

Такой интервал называется доверительным интервалом (confidence interval), вероятность Q – доверительной вероятностью.

Поскольку границы доверительного интервала являются функциями выборочных значений, они случайны. Поэтому говорят, что доверительный интервал накрывает значение искомой генеральной характеристики (параметра) с вероятностью, не меньшей, чем Q.